Annu. Rev. Astron. Astrophys. 2005. 43: 861-918 Copyright © 2005 by Annual Reviews. All rights reserved

1. WHAT ARE THE DAMPED Ly SYSTEMS AND HOW ARE THEY FOUND?

Damped Ly systems are a class of QSO absorbers selected for the presence of H I column densities, N(H I) 2 × 10²⁰ cm^-2. This criterion differs from those used to find other classes of QSO absorbers selected on the basis of H I content. The Ly forest absorbers, reviewed in this journal by Rauch (1998), are selected for N(H I) < 10¹⁷ cm^-2, while the Lyman limit systems have 10¹⁷ < N(H I) < 2 × 10²⁰ cm^-2 (Peroux et al. 2003). The Ly forest absorbers are optically thin at the Lyman limit, since the column density N(H I) = 10¹⁷ cm^-2 corresponds to about unity optical depth at the Lyman limit. Are these absorbers physically different from the damped systems or have the column-density criteria resulted in arbitrary distinctions? In fact there is a fundamental difference: hydrogen is mainly neutral in damped Ly systems, while it is ionized in all other classes of QSO absorption systems. This includes absorbers selected for the presence of C IV 1548.1, 1550.7 resonance-line doublets (Sargent, Steidel & Boksenberg 1988), Mg II 2796.3, 2803.5 resonance-line doublets (Steidel & Sargent 1992) and Lyman limit absorption (Prochaska 1999), which do not also qualify as damped Ly systems.

The neutrality of the gas is crucial: while stars are unlikely to form out of warm ionized gas, they are likely to descend from cold neutral clouds, which are the precursors of molecular clouds, the birthplace of stars (Wolfire et al. 2003). This property takes on added significance when it is realized that the damped Ly systems dominate the neutral-gas content of the Universe in the redshift interval z = [0, 5], and at z ~ 3.0-4.5 contain sufficient mass in neutral gas to account for a significant fraction of the visible stellar mass in modern galaxies (e.g., Storrie-Lombardi & Wolfe 2000). This has led to the widely accepted idea that damped Ly systems serve as important neutral-gas reservoirs for star formation at high redshifts (e.g., Nagamine, Springel & Hernquist 2004a). Moreover, as repositories of significant amounts of metals the damped Ly systems have been used to trace the age-metallicity relationship and other aspects of galactic chemical evolution (Pei, Fall & Hauser 1999; Pettini 2004; Pettini et al. 1994; Prochaska et al. 2003a).

The purpose of this review is to present an overview of the damped Ly systems. Current research on the high-redshift Universe is dominated by surveys that rely on the detection of radiation emitted by stars (e.g., Dickenson et al. 2003, Giavalisco et al. 2004, Steidel et al. 2003) or ionized gas (e.g., Ouchi et al. 2003, Rhoads & Malhotra 2001). By contrast, damped Ly systems provide a window on the interplay between neutral gas and newly formed stars, i.e., the damped Ly systems are the best, perhaps the only, examples we have of an interstellar medium in the high-redshift Universe. Consequently, the focus of this review will be on the manner in which damped Ly systems trace, and play an active role in, cosmic star formation and hence galaxy formation.

Throughout this review we adopt a cosmology consistent with the WMAP (Bennett et al. 2003) results, _m, , h) = (0.3, 0.7, 0.7).

1.1. History of Damped Ly Surveys

To understand the significance of damped Ly systems for research in galaxy formation we give a brief historical perspective.

The motivation for the first damped Ly survey was to find the neutral-gas disks of galaxies at high redshifts (Wolfe et al. 1986). Unlike today, the cold dark matter (hereafter CDM) paradigm of hierarchical structure formation (i.e., merging protogalactic clumps) did not dominate theories of galaxy formation in the early 1980s. Rather, the idea of mature galaxy disks at high redshift fitted in with the coherent collapse model of Eggen, Lynden-Bell & Sandage (1962; also Fall & Efstathiou 1980), which was highly influential at the time. Some QSO absorbers with properties resembling galaxy disks had been found at z < 1 through the detection of 21 cm absorption either in radio-frequency scanning surveys (Brown & Roberts 1973) or at the redshifts of Mg II-selected absorbers (Roberts et al. 1976). However, application of these techniques resulted in only a few detections. While it was unclear whether the 21 cm absorbers belonged to a new population of objects or were rarely occurring oddities, the radio scanning techniques were valuable for successfully detecting cold, quiescent gas at large redshifts for the first time. Specifically, Brown & Roberts (1973) and Brown & Mitchell (1983) used this technique to detect two 21 cm lines with FWHM velocity widths, v_{H I} 10 and 20 km s^-1. The temperature of the gas detected in 21 cm absorption is likely to be low because the 21 cm optical depth ₂₁ N(H I) / (T_s v_{H I}), where the hyperfine spin temperature, T_s, generally equals the kinetic temperature of the cold, dense gas detected in 21 cm absorption.

However, the most efficient method for locating quiescent layers of neutral gas is through the detection of damped Ly absorption lines. In the rest frame of the atom, the absorption profile of any atomic transition is naturally broadened owing to the finite lifetime of the upper energy state. In the rest frame defined by the average velocity of the gas, the natural profile is Doppler broadened by the random motions of the atoms: the convolution of both effects results in the Voigt profile (e.g., Mihalas 1978). Because the Doppler profile falls off from the central frequency, ₀, as exp[-( / _D)²] (where = | - ₀| and _D = (2)^1/2 _{v 0} / c for an assumed Gaussian velocity distribution with dispersion _v) and the natural or "damped" absorption profile falls off from ₀ like 1 / ( )², at sufficiently large the probability for damped absorption exceeds the probability for absorption in the Doppler profile. The frequency intervals in which natural broadening dominates Doppler broadening are called the damping wings of the profile function. Most atomic transitions of abundant ions are optically thin in their damping wings but optically thick near the core of the Doppler profile. The latter transitions have unit optical depth at _{= 1 D} × [ln N(X^j)]^1/2, where N(X^j) is the column density of ionic species X^j. Such lines are saturated. The reason is that the rest-frame equivalent width of an absorption line is given by W_r ( / ) (1- exp(-) d ), and therefore W_r is proportional to _{= 1}. In the case of lines with unit optical depth near the Doppler core the line is saturated because W_r is insensitive to the value of N(X^j). Due to the higher values of N(H I), Ly has unit optical depth in the damping wings at ₌₁ [A₂₁ f₂₁ N(H I)]^1/2 when N(H I) 10¹⁹ cm^-2 and _v < 70 km s^-1: A₂₁ and f₂₁ are the Einstein spontaneous emission coefficient and oscillator strength for the Ly transition, respectively. In this case, unit optical depth occurs in the damping wings, and therefore the equivalent width of a damped Ly line is independent of the velocity structure of the gas for velocity dispersions within the range detected in most QSO absorption systems. As a result, the equivalent width will be large even when the velocity dispersion is small.

By the early 1980s only four damped Ly systems had been found. In every case they were high-column-density systems, N(H I) 10²¹ cm^-2, which were found by chance (Beaver et al. 1972; Carswell et al. 1975; Smith, Margon & Jura 1979; Wright et al. 1979). Although the sample was sparse, the utility of the damped Ly criterion was demonstrated when 21 cm absorption at z ~ 2 was detected in two of the three background QSOs that were radio sources (Wolfe, Briggs & Jauncey 1981; Wolfe & Davis 1979). The narrow line widths, v_{H I} 20 km s^-1 (where v_{H I} = (8 ln 2)^1/2 _v), and relatively low spin temperatures, T_s < 1000 K, implied that these absorbers were H I layers in which the gas was cold and quiescent.

For these reasons Wolfe et al. (1986) began a survey for damped Ly systems by acquiring spectra of large numbers of QSOs and then searching them for the presence of damped Ly absorption lines. The survey for damped Ly systems had several advantages over surveys for 21 cm absorption lines. For example, the redshift interval covered by a single optical spectrum, z 1, is large compared to that sampled by bandpasses then available for 21 cm surveys, z 0.02. Second, optical spectra of QSOs are obtained toward continuum sources with diameters less than 1 pc, whereas the diameters of the associated background radio sources typically exceed 100 pc at the low frequencies of redshifted 21 cm lines. As a result the survey was capable of detecting compact gaseous configurations with low surface covering factors that would have been missed in 21 cm surveys. Another advantage of optical surveys is the large oscillator strength, f₂₁ = 0.418, of the Ly transition (by comparison f₂₁ = 2.5 × 10^-8 times a stimulated emission correction of 0.068 K / T_s for the 21 cm line), which allows for the detection of warm H I, which is optically thin to 21 cm absorption owing to high values of T_s but optically thick in Ly. But this is also a disadvantage: the strength of the Ly transition combined with the high abundance of hydrogen means that the more frequently occurring low-column-density clouds in which H is mainly ionized will be optically thick in Ly. The result is a profusion of Ly absorption lines, i.e., the Ly forest, which dominate the absorption spectrum blueward of Ly emission (Figure 1). Although the Ly forest lines act as excellent probes of the power spectrum and other cosmological quantities (see McDonald 2003, Tytler et al. 2004), they are potential sources of confusion noise for the detection of damped Ly lines, especially at z > 4, since the line density per unit redshift increases with redshift. Identification of damped Ly lines at z > 5.5 is essentially impossible because of Ly forest confusion noise.

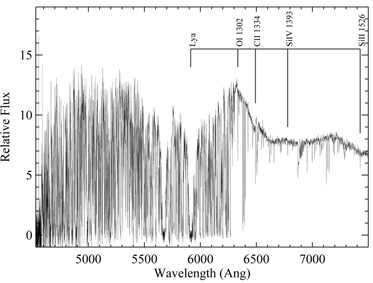Figure 1. Keck/ESI spectrum of QSO PSS0209 + 0517 showing the Ly forest, a pair of damped Ly systems, and a series of metal lines. The schematic labeling in the figure identifies several key features for the damped Ly system at z = 3.864. The absorption trough at = 5674 Å corresponds to the damped Ly line at z = 3.667.

However, at z < 5.5 the large column densities of H I in galaxy disks or in any other configuration produce damped Ly absorption lines that are strong enough to be distinguished from the Ly forest (Figure 1). Consider the equivalent widths. At the time of the Wolfe et al. (1986) survey the most accurate 21 cm maps of spiral galaxies were obtained with the Westerbork radio interferometer. These showed the H I column densities of galaxy disks to decrease from N(H I) ~ 10²¹cm^-2 at their centers to N(H I) = 2 × 10²⁰ cm^-2 at a limiting radius R_l = (1.5 ± 0.5) R_26.5, which was set by the sensitivity available with Westerbork and comparable radio antennas. Here the Holmberg radius, R_26.5, is the radius at which the B band surface brightness equals 26.5 mag arcsec^-2 (Bosma 1981). The rest-frame equivalent width of a damped Ly line created by an H I column density, N(H I), is given by W_r 10 × [N(H I)/2 × 10²⁰ cm^-2]^1/2 Å. Because the observed equivalent width of a line formed at redshift z is W_obs = (1 + z) W_r, damped Ly systems with N(H I) 2 × 10²⁰ cm^-2 will appear in optical QSO spectra with W_obs 16 Å for damped Ly systems redshifted redward of the atmospheric cutoff (i.e., z 1.6 for _atm = 3200 Å). Lines this strong are easily distinguishable from the W_obs 3 Å equivalent widths of typical Ly forest lines. Furthermore, they can be detected at low resolution and moderate signal-to-noise ratio. Since the goal of the first survey for damped Ly systems was to find absorbers with N(H I) 2 × 10²⁰ cm^-2, a spectral resolution, = 10 Å, was sufficient for resolving candidate features.

1.2. Modern Surveys and Identification of Damped Ly Systems

Since the initial survey was published, nine more surveys have been completed for damped Ly systems with N(H I) 2 × 10²⁰ cm^-2 (Ellison et al. 2001; Lanzetta et al. 1991; Lanzetta, Wolfe & Turnshek 1995; Péroux et al. 2003b; Prochaska & Herbert-Fort 2004; Prochaska, Herbert-Fort & Wolfe 2005; Rao & Turnshek 2000; Storrie-Lombardi & Wolfe 2000; Wolfe et al. 1995). The identification of damped Ly systems is more complex than for other classes of QSO absorbers. The Ly forest "clouds," which dominate the absorption spectrum blueward of Ly emission, are abundant and easy to identify. Similarly, surveys for C IV or Mg II absorption systems rely on the detection of doublets with known wavelength ratios, which are straightforward to locate redward of Ly emission. By contrast, the task of surveys for damped Ly systems is to pick out a single damped Ly line from the confusion noise generated by the Ly forest. In particular, one must distinguish a single, strong Ly absorption line created in high-column-density gas with low-velocity dispersion, but broadened by radiation damping, from strong Ly absorption features that are Doppler-broadened blends of several lines arising from redshift systems with low-column-density gas. The presence of narrow Ly forest absorption lines in the damping wings of the absorption profile is a further complication that can distort the shape of the true line profile in data of moderate or low signal-to-noise ratios (see Figure 2 for examples).

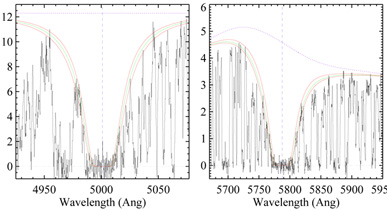Figure 2. Example Voigt profile fits to two damped Ly systems of the sample from Prochaska et al. (2003b). The vertical dashed line indicates the line centroid determined from metal-line transitions identified outside the Ly forest. The dotted line traces the continuum of the QSO and the green and red lines trace the Voigt profile solution and the fits corresponding to 1 changes to N(HI). The fluctuations at the bottom of the damped Ly absorption troughs indicate the level of sky noise.

The most widely used strategy for discovering damped Ly systems was first introduced by Wolfe et al. (1986) and later refined by Lanzetta et al. (1991) and Wolfe et al. (1995). First, a continuum is fitted to the entire QSO spectrum blueward of Ly emission. Then damped Ly candidates are identified as absorption features with rest equivalent widths W_r exceeding W_thresh = 5 Å. This conservative criterion corresponds to N(H I) 5 × 10¹⁹ cm^-2, which guarantees that few systems with N(H I) above the completeness limit of 2 × 10²⁰ cm^-2 will be missed. The search is carried out in the redshift interval z = [z_min, z_max], where z_min is generally the shortest wavelength for which (W_r) < 1 Å and z_max is set 3000 km s^-1 below z_em to avoid contamination by the background QSO. Finally, a Voigt profile is fitted to the Ly profile to determine the value of N(H I). Where possible, the centroid is identified from the redshift determined by metal lines outside the Ly forest. This is particularly important at z 3 where line-blending from the Ly forest often contaminates the damping wings (e.g., Figure 2). The surveys were time-consuming because the signal-to-noise ratio and resolution of the spectra used to acquire damped Ly system candidates were usually inadequate for fitting Voigt profiles to the data. Therefore, follow-up spectroscopy at higher spectral resolution and with longer integration times was usually necessary.

Recently, Prochaska & Herbert-Fort (2004) and Prochaska, Herbert-Fort & Wolfe (2005) have streamlined this process in a survey based on a single set of QSO spectra drawn from the Sloan SDSS archive (Abazajian et al. 2003). Because of the high-quality, good spectral resolution (R ~ 2000) and extended spectral coverage of the data, the authors could fit accurate Voigt profiles to the same data used to find damped Ly system candidates. The authors also bypass the time-consuming step of fitting a continuum to the QSO spectrum blueward of Ly emission by searching for damped Ly system candidates in spectral regions with lower-than-average signal-to-noise ratios, i.e., regions coinciding with broad absorption troughs. The survey is not formally complete to N(H I) = 2 × 10²⁰ cm^-2, but the similarity between d / dX, the number of damped Ly systems encountered per unit absorption distance along the line of sight (see Section 2.1), in their survey and previous surveys suggests that the Prochaska, Herbert-Fort & Wolfe (2005) survey is more than 95% complete. The number of damped Ly systems for the SDSS DR2 and DR3 archives is 525. As a result, the number of damped Ly systems in a statistically complete sample now excedes previous samples by an order of magnitude at z ~ 3 and several times at z ~ 4.

While the H I selection methods are successful at finding damped Ly systems at z 1.6, they have been unsuccessful at finding large numbers of objects at lower redshifts. This is partly due to the reduced interception probability per unit redshift at low z and partly because few QSOs have been observed from space at UV wavelengths, which is required to detect Ly at z < 1.6. To increase the number of low-redshift damped Ly systems from the two confirmed objects detected in previous H I selected surveys (see Lanzetta, Wolfe & Turnshek 1995), Rao & Turnshek (2000) searched for damped Ly systems in samples of QSO absorption systems selected for Mg II 2796.3, 2803.5 absorption. Since Mg II absorption is present in every damped system in which it could be observed, it turns out to be a reliable indicator for the presence of damped Ly. Using this technique, Rao, Turnshek, and collaborators have recently increased the sample size to 41 damped Ly systems with z < 1.6 (SM Rao, DA Turnshek & DB Nestor, private communication).

The current sample of damped Ly systems that are drawn from surveys with statistically complete selection criteria comprises over 600 redshift systems. While the number of damped Ly systems is smaller than the 2350 objects comprising the population of known Lyman Break Galaxies (Steidel et al. 2003), we expect the damped Ly system population to approach this number when all QSO spectra from the Sloan database become available.

1.3. The Significance of the N(H I) 2 × 10²⁰ cm^-2 Survey Threshold

The survey statistics cited above refer only to systems with N(H I) 2 × 10²⁰ cm^-2, which is a historical threshold set by the H I properties of nearby spiral galaxies (see Section 1.1). Because the nature of damped Ly systems is still not understood, their H I properties may differ from those of nearby H I disks: for example, CDM cosmogonies envisage damped Ly systems as merging protogalactic clumps (Haehnelt, Steinmetz & Rauch 1998). As a result, it is reasonable to ask whether the 2 × 10²⁰ cm^-2 threshold is the appropriate one. Indeed, since the empirically determined frequency distribution of H I column densities increases with decreasing N(H I) (Figure 3), lower H I thresholds would be advantageous because they would result in larger samples.

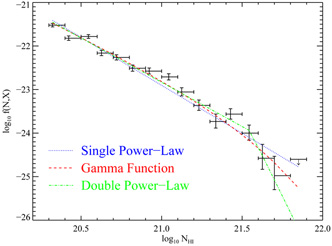Figure 3. The N(HI) frequency distribution f(N, X) determined by Prochaska, Herbert-Fort & Wolfe (2005) for all damped Ly systems in the SDSS-DR3_4 sample. Overplotted on the data points are a single power-law, -function, and a double power-law. Only the latter two are acceptable fits to the data. Plot taken from Prochaska, Herbert-Fort & Wolfe (2005).

Fortuitously, the 2 × 10²⁰ cm^-2 threshold is optimal for physical reasons unrelated to the properties of galaxy disks. Rather, at large redshifts it is the column density that distinguishes neutral gas from ionized gas: at N(H I) < 2 × 10²⁰ cm^-2 the gas is likely to be ionized while at N(H I) > 2 × 10²⁰ cm^-2 it is likely to be neutral. The minimal source of ionization is background radiation due to the integrated population of QSOs and galaxies. Using background intensities computed by Haardt & Madau (1996, 2003), Viegas (1995) and Prochaska & Wolfe (1996) show that the gas in most of the "sub-damped Ly" population [defined to have 10¹⁹ < N(H I) < 2 × 10²⁰ cm^-2] described by Péroux et al. (2002, 2003a) is in fact significantly ionized with temperature, T > 10⁴ K. This is a problem since gas neutrality is a necessary condition if damped Ly systems are to serve as neutral gas reservoirs for star formation at high redshift, a defining property of the population. For this reason the comoving density of H I comprising the sub-damped Ly population discussed by Péroux et al. (2003b) should not be included in the census of gas available for star formation. As a result, the sub-damped Ly correction to the comoving density of neutral gas, _g(z), should be ignored. We suggest that these ionization levels make "super Lyman-limit system" a more appropriate name for systems with 10¹⁹< N(H I) < 2 × 10²⁰ cm^-2.