Copyright © 2005 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2005. 43:
861-918 Copyright © 2005 by Annual Reviews. All rights reserved |
 SYSTEMS
SYSTEMS
Several lines of evidence imply that damped
Ly systems experience
ongoing star formation. At z < 1.6 the evidence is
unambiguous, since more than half of the sample is associated with
galaxies of stars. At z
systems experience
ongoing star formation. At z < 1.6 the evidence is
unambiguous, since more than half of the sample is associated with
galaxies of stars. At z
 1.6 the evidence is
indirect because only one damped
Ly
1.6 the evidence is
indirect because only one damped
Ly system is identified
with a resolved object of galactic dimensions that emits
starlight. While starlight likely ionizes the gas that gives rise to
Ly
system is identified
with a resolved object of galactic dimensions that emits
starlight. While starlight likely ionizes the gas that gives rise to
Ly emission in two other
high-z damped
Ly
emission in two other
high-z damped
Ly systems, the
starlight itself has not been directly detected. The expectation is that
most of the metals seen in damped
Ly
systems, the
starlight itself has not been directly detected. The expectation is that
most of the metals seen in damped
Ly systems were
generated through star formation in their host systems, but the
instantaneous (SFRs) characterizing this important population of objects
remained unknown until recently.
systems were
generated through star formation in their host systems, but the
instantaneous (SFRs) characterizing this important population of objects
remained unknown until recently.
8.1. Direct Emission Measurements of Star-Formation
Rates in Damped
Ly Systems with z
> 1.6
Systems with z
> 1.6
Table 1 summarizes results including
SFRs for the three positive detections and for objects with upper limits
on SFR at z  1.6. Observed lower limits on
L(H
1.6. Observed lower limits on
L(H ) were
coverted to upper limits on SFR using the
Kennicutt (1998)
calibration, SFR
(M
) were
coverted to upper limits on SFR using the
Kennicutt (1998)
calibration, SFR
(M year-1) = 7.9 × 10-42 L
(H
year-1) = 7.9 × 10-42 L
(H  )(ergs
s-1). Detections of
Ly
)(ergs
s-1). Detections of
Ly emission
7 were combined with the
expression for L (H
emission
7 were combined with the
expression for L (H ) and
case B radiative recombination to find lower limits of SFR
(M
) and
case B radiative recombination to find lower limits of SFR
(M year-1) = 1.1 × 10-42
L(Ly
year-1) = 1.1 × 10-42
L(Ly ) (ergs
s-1). The total magnitude integrated over DLA2206 - 19A of
V = 23 and the very sensitive B > 27 limit on DLA0953 +
47A (A. Bunker 2004, priv. comm.) were combined with the rest-frame UV
Kennicutt (1998)
calibration, SFR
(M
) (ergs
s-1). The total magnitude integrated over DLA2206 - 19A of
V = 23 and the very sensitive B > 27 limit on DLA0953 +
47A (A. Bunker 2004, priv. comm.) were combined with the rest-frame UV
Kennicutt (1998)
calibration, SFR
(M year-1) = 1.4 × 10-28
L
year-1) = 1.4 × 10-28
L (ergs s-1
Hz-1), to set a lower limit on the SFR for DLA2206 - 19A and
a rough upper limit for DLA0953 + 47A assuming no dust extinction for
the latter object. An estimated dust extinction correction for DLA2206 -
19A
(Wolfe et al. 2004)
suggests an upper limit on SFR of 50
M
(ergs s-1
Hz-1), to set a lower limit on the SFR for DLA2206 - 19A and
a rough upper limit for DLA0953 + 47A assuming no dust extinction for
the latter object. An estimated dust extinction correction for DLA2206 -
19A
(Wolfe et al. 2004)
suggests an upper limit on SFR of 50
M year-1, which is comparable to the SFRs of the more luminous
Lyman Break Galaxies
(Shapley et al. 2003).
year-1, which is comparable to the SFRs of the more luminous
Lyman Break Galaxies
(Shapley et al. 2003).
8.2. Star-Formation Rates from the C II* Technique
A method recently developed by
Wolfe, Prochaska & Gawiser
(2003)
makes it possible to infer the SFR per unit area for individual damped
Ly systems. The basic
method is to use measurements of the C II* 1335.7 column density to
measure the [C II] 158 µm cooling rate in the neutral gas
producing the damped
Ly
systems. The basic
method is to use measurements of the C II* 1335.7 column density to
measure the [C II] 158 µm cooling rate in the neutral gas
producing the damped
Ly absorption. This is
possible because the C II*
absorption. This is
possible because the C II*
 1335.7 transition
arises from the excited 2P3/2 state in
C+, and spontaneous photon decay of the
2P3/2 state to the
2P1/2 state results in [C II] 158
µm emission, which is the principal coolant of neutral gas
in the Galactic ISM
(Wright et al. 1991).
Under the presumed condition of thermal balance, the cooling rate equals
the heating rate and it is possible to calculate the SFR per unit area
that generates the implied heating rate.
1335.7 transition
arises from the excited 2P3/2 state in
C+, and spontaneous photon decay of the
2P3/2 state to the
2P1/2 state results in [C II] 158
µm emission, which is the principal coolant of neutral gas
in the Galactic ISM
(Wright et al. 1991).
Under the presumed condition of thermal balance, the cooling rate equals
the heating rate and it is possible to calculate the SFR per unit area
that generates the implied heating rate.
By analogy with the Galactic ISM,
Wolfe, Prochaska & Gawiser
(2003) adopt the grain photoelectric effect as the principal heating
mechanism for damped
Ly systems. In that case
FUV radiation
(h
systems. In that case
FUV radiation
(h
 6-13.6 eV) ejects
photoelectrons from grain surfaces, which heat ambient electrons through
Coulomb interactions
(Bakes & Tielens 1994,
Weingartner & Draine
2003).
The heating rate from the grain photoelectric effect is proportional to
the FUV radiation intensity
J
6-13.6 eV) ejects
photoelectrons from grain surfaces, which heat ambient electrons through
Coulomb interactions
(Bakes & Tielens 1994,
Weingartner & Draine
2003).
The heating rate from the grain photoelectric effect is proportional to
the FUV radiation intensity
J ,
which consists of a contribution from the FUV background radiation plus
a local contribution from hot stars located inside the galaxy that is
proportional to the instantaneous SFR per unit area,
,
which consists of a contribution from the FUV background radiation plus
a local contribution from hot stars located inside the galaxy that is
proportional to the instantaneous SFR per unit area,
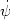 *.
*.
To infer
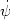 *
and other properties from observations,
Wolfe, Prochaska &
Gawiser (2003)
deduce the [C II] 158 µm spontaneous emission rate per H
atom from the observational quantity:
*
and other properties from observations,
Wolfe, Prochaska &
Gawiser (2003)
deduce the [C II] 158 µm spontaneous emission rate per H
atom from the observational quantity:
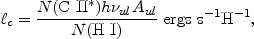 |
(8) |
where Aul is the Einstein coefficient and
h ul is the
energy of the 158 µm transition. These are known quantities,
and N(C II*) and N(HI) are measured from the
absorption line spectra. The total heating rate includes inputs due to
the grain photoelectric effect, X-ray photoionization, cosmic ray
ionization, C I photoionization, and collisional heating. The total
cooling rate includes cooling due to
Ly
ul is the
energy of the 158 µm transition. These are known quantities,
and N(C II*) and N(HI) are measured from the
absorption line spectra. The total heating rate includes inputs due to
the grain photoelectric effect, X-ray photoionization, cosmic ray
ionization, C I photoionization, and collisional heating. The total
cooling rate includes cooling due to
Ly , grain radiative
recombination, and emission by fine-structure states of O0,
Si+, Fe+, etc., in addition to the [C II] 158
µm fine-structure emission. Radiative excitation of the
C+ fine-structure states by CMB radiation is included because
it can be significant at high redshift.
Wolfe et al. (2004)
showed that the heating rates predicted for the
Haardt & Madau (2003)
backgrounds were significantly lower than the 158 µm cooling
rates implied for damped
Ly
, grain radiative
recombination, and emission by fine-structure states of O0,
Si+, Fe+, etc., in addition to the [C II] 158
µm fine-structure emission. Radiative excitation of the
C+ fine-structure states by CMB radiation is included because
it can be significant at high redshift.
Wolfe et al. (2004)
showed that the heating rates predicted for the
Haardt & Madau (2003)
backgrounds were significantly lower than the 158 µm cooling
rates implied for damped
Ly systems with detected
C II*
systems with detected
C II* 1335.7
absorption, requiring active star formation to explain the observed
cooling rates. On the other hand,
Wolfe et al. (2004)
also showed that heating by background radiation alone cannot be ruled
out for systems in which
C II*
1335.7
absorption, requiring active star formation to explain the observed
cooling rates. On the other hand,
Wolfe et al. (2004)
also showed that heating by background radiation alone cannot be ruled
out for systems in which
C II* 1335.7
absorption was not detected. A summary of the
1335.7
absorption was not detected. A summary of the
 c data for damped
Ly
c data for damped
Ly systems (and the
Galaxy) is given in Figure 12.
Wolfe, Prochaska & Gawiser
(2003)
argued that the heating rate in the Galaxy is much larger than that in
damped Ly
systems (and the
Galaxy) is given in Figure 12.
Wolfe, Prochaska & Gawiser
(2003)
argued that the heating rate in the Galaxy is much larger than that in
damped Ly systems
because the dust content in the Galaxy is at least a factor of 30 higher
than that in damped
Ly
systems
because the dust content in the Galaxy is at least a factor of 30 higher
than that in damped
Ly systems, whereas
systems, whereas
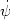 *
in the Galaxy is only a factor of 2 to 3 lower than that in damped
Ly
*
in the Galaxy is only a factor of 2 to 3 lower than that in damped
Ly systems (see below).
systems (see below).
In the case of systems with detected
C II* 1335.7
absorption, one compares 158 µm emission rates computed for
a range of SFRs per unit area with the empirical quantity,
1335.7
absorption, one compares 158 µm emission rates computed for
a range of SFRs per unit area with the empirical quantity,
 c. This results
in two solutions for
c. This results
in two solutions for
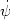 *
corresponding to thermally stable states of a two-phase medium in which
warm neutral medium (WNM) gas is in pressure equilibrium with cold
neutral medium (CNM) gas: the WNM solution corresponds to the gas with
T ~ 8000 K and n ~ 0.02 cm-3, and the CNM
solution corresponds to the gas with T ~ 100 K and n ~
10 cm-3. In every case the WNM solution for
*
corresponding to thermally stable states of a two-phase medium in which
warm neutral medium (WNM) gas is in pressure equilibrium with cold
neutral medium (CNM) gas: the WNM solution corresponds to the gas with
T ~ 8000 K and n ~ 0.02 cm-3, and the CNM
solution corresponds to the gas with T ~ 100 K and n ~
10 cm-3. In every case the WNM solution for
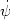 *
is a factor of 10 or more higher than the CNM solution: since C II
emission in the WNM is a small fraction of the total cooling rate, the
total heating rate implied for an observed value of
*
is a factor of 10 or more higher than the CNM solution: since C II
emission in the WNM is a small fraction of the total cooling rate, the
total heating rate implied for an observed value of
 c must be higher
in the WNM than in the CNM. Owing to the low dust optical depths of
damped
Ly
c must be higher
in the WNM than in the CNM. Owing to the low dust optical depths of
damped
Ly systems the resulting
systems the resulting
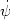 *
are system-wide average SFRs rather than local values as is the case in
the dusty Galactic ISM.
*
are system-wide average SFRs rather than local values as is the case in
the dusty Galactic ISM.
This method was used by
Wolfe et al. (2004)
to analyze a sample of 45 damped
Ly systems, 23 with
measured C II* column densities and 22 for which C II* was not
detected. In the redshift interval z = [1.6, 4.5] the average SFR
per unit area for positive detections is
<
systems, 23 with
measured C II* column densities and 22 for which C II* was not
detected. In the redshift interval z = [1.6, 4.5] the average SFR
per unit area for positive detections is
<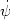 *> = 11.3 × 10-3
M
*> = 11.3 × 10-3
M year-1 kpc-2 for the CNM solution and 0.21
M
year-1 kpc-2 for the CNM solution and 0.21
M year-1 kpc-2 for the WNM solution; by comparison
with the Galaxy
year-1 kpc-2 for the WNM solution; by comparison
with the Galaxy
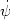 *
*
 4 ×
10-3
M
4 ×
10-3
M year-1 kpc-2. However, the WNM solution is
unlikely to be correct because the bolometric background intensity
produced exceeds the observational limits (see
Wolfe, Gawiser &
Prochaska 2003).
This conclusion is consistent with recent evidence from individual
systems;
Howk, Wolfe & Prochaska
(2005)
showed that the low upper limit on the optical-depth ratio of Si II*
year-1 kpc-2. However, the WNM solution is
unlikely to be correct because the bolometric background intensity
produced exceeds the observational limits (see
Wolfe, Gawiser &
Prochaska 2003).
This conclusion is consistent with recent evidence from individual
systems;
Howk, Wolfe & Prochaska
(2005)
showed that the low upper limit on the optical-depth ratio of Si II*
 1264.7 to C II*
1264.7 to C II*
 1335.7 in a
high-redshift damped
Ly
1335.7 in a
high-redshift damped
Ly system results in an
upper limit of 800 K for the temperature in the gas producing C II*,
which implies that C II* absorption arises in CNM gas in this
system. Furthermore, a pure WNM solution would significantly overpredict
the observed rest-frame-UV luminosity from DLA2206 - 19A based on its
measured
system results in an
upper limit of 800 K for the temperature in the gas producing C II*,
which implies that C II* absorption arises in CNM gas in this
system. Furthermore, a pure WNM solution would significantly overpredict
the observed rest-frame-UV luminosity from DLA2206 - 19A based on its
measured
 c, implying that
C II* absorption in this damped
Ly
c, implying that
C II* absorption in this damped
Ly system arises in a
CNM. It is significant that the
predicted value for CNM,
J
system arises in a
CNM. It is significant that the
predicted value for CNM,
J CII* =
1.7+2.7-1.0 × 10-18 ergs
cm-2 s-1 Hz-1 sr-1, is the
largest mean intensity inferred from the entire C II* sample. This may
help explain why DLA2206 - 19A is one of the rare damped
Ly
CII* =
1.7+2.7-1.0 × 10-18 ergs
cm-2 s-1 Hz-1 sr-1, is the
largest mean intensity inferred from the entire C II* sample. This may
help explain why DLA2206 - 19A is one of the rare damped
Ly systems detected in
emission.
systems detected in
emission.
On the other hand, the gas detected in absorption is more likely to be a
WNM for damped
Ly systems with upper
limits on C II* absorption. In this case the gas could be a pure
single-phase WNM heated by background radiation alone. These damped
Ly
systems with upper
limits on C II* absorption. In this case the gas could be a pure
single-phase WNM heated by background radiation alone. These damped
Ly systems would then be
objects without significant star formation at the absorption epochs. Or
the gas could be the WNM branch of a two-phase medium in which the SFR
per unit area is similar to that found for the CNM solutions
(Wolfe et al. 2004).
While the absence of 21 cm absorption at z > 3
(Kanekar & Chengalur
2003)
and the large C II/C I ratios
(Liszt 2002)
are consistent with the WNM hypothesis, both phenomena are also
naturally explained within the context of the two-phase
hypothesis. Clearly, it is important to determine which of these
explanations is the correct one.
systems would then be
objects without significant star formation at the absorption epochs. Or
the gas could be the WNM branch of a two-phase medium in which the SFR
per unit area is similar to that found for the CNM solutions
(Wolfe et al. 2004).
While the absence of 21 cm absorption at z > 3
(Kanekar & Chengalur
2003)
and the large C II/C I ratios
(Liszt 2002)
are consistent with the WNM hypothesis, both phenomena are also
naturally explained within the context of the two-phase
hypothesis. Clearly, it is important to determine which of these
explanations is the correct one.
The C II* technique can also be used to obtain quantities with
cosmological significance. Specifically, the SFR per unit comoving
volume is given by  * = <
* = <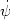 *(z)>(A*
/ Ap)(d
*(z)>(A*
/ Ap)(d / dX)(H0 / c), where
A* is the intrinsic cross-sectional area
occupied by stars emitting FUV radiation and Ap is the
projection of the intrinsic H I area, AHI, on the sky.
8 In the uniform disk
model, neutral gas and stars are uniformly distributed across
AHI, yielding the values for
/ dX)(H0 / c), where
A* is the intrinsic cross-sectional area
occupied by stars emitting FUV radiation and Ap is the
projection of the intrinsic H I area, AHI, on the sky.
8 In the uniform disk
model, neutral gas and stars are uniformly distributed across
AHI, yielding the values for
 * (z) given in
Table 2, which also summarizes the systematic
uncertainties discussed at length in
Wolfe, Gawiser &
Prochaska (2003).
* (z) given in
Table 2, which also summarizes the systematic
uncertainties discussed at length in
Wolfe, Gawiser &
Prochaska (2003).
| Property | 0.0-1.6 | 1.6-4.5 |
d / dX
/ dX |
.... | 0.077 ± 0.016 b |
103
 g(z) g(z) |
0.96 ± 0.23 a | 0.92 ± 0.21 b |
log10
 *(z) *(z) |
< -1.40 | -0.70 ± 0.28c |
| < Z > | -0.81 ± 0.032 | -1.33 ± 0.09 |
a Due to large uncertainties
in individual measurements, error
in mean given by propagation of experimental errors.
| ||
The total mass of stars produced in damped
Ly systems as a function
of redshift can be computed by integrating over the cosmic
star-formation history of damped
Ly
systems as a function
of redshift can be computed by integrating over the cosmic
star-formation history of damped
Ly systems. The mass
density of stars predicted by today, including the contribution from
"normal" galaxies at z < 1.6, is consistent with the total
current density of stars in spiral and elliptical galaxies, but this
does not reveal the precise population of stars produced by
high-redshift damped
Ly
systems. The mass
density of stars predicted by today, including the contribution from
"normal" galaxies at z < 1.6, is consistent with the total
current density of stars in spiral and elliptical galaxies, but this
does not reveal the precise population of stars produced by
high-redshift damped
Ly systems. The same
star-formation history will also deplete the neutral gas reservoir at
high redshift in about t*
systems. The same
star-formation history will also deplete the neutral gas reservoir at
high redshift in about t*
 2 Gyr, i.e.,
2 Gyr, i.e.,
 g(z)
would vanish by z
g(z)
would vanish by z
 2 if star formation
starts at z
2 if star formation
starts at z
 5. Instead
5. Instead
 g(z)
drops by a factor of two during this time, which argues for
replenishment of neutral gas at an accretion rate
g(z)
drops by a factor of two during this time, which argues for
replenishment of neutral gas at an accretion rate
 a(z)
a(z)
 0.5
0.5
 *(z).
*(z).
Wolfe, Gawiser &
Prochaska (2003)
also calculated the mass density of metals produced in damped
Ly systems by using the
conversion of SFR to metal formation rate suggested by
Madau et al. (1996) and
Pettini (1999),
systems by using the
conversion of SFR to metal formation rate suggested by
Madau et al. (1996) and
Pettini (1999),
 metals = (1/42)
metals = (1/42)
 *.
Extrapolating to the present day, including the contribution from star
formation in normal galaxies at z < 1.6, yields a mass of metals
a few times larger than that found in spiral bulges today, which seems
feasible. Integrating under the DLA cosmic star-formation history at
z
*.
Extrapolating to the present day, including the contribution from star
formation in normal galaxies at z < 1.6, yields a mass of metals
a few times larger than that found in spiral bulges today, which seems
feasible. Integrating under the DLA cosmic star-formation history at
z
 2.5 predicts a factor of 30
higher cosmic mean metallicity due to metal enrichment of neutral gas
than is observed in damped
Ly
2.5 predicts a factor of 30
higher cosmic mean metallicity due to metal enrichment of neutral gas
than is observed in damped
Ly systems at z =
2.5
(Prochaska et al. 2003a).
This sort of "missing metals" problem was first identified by
Pettini (1999)
for Lyman Break Galaxy SFRs compared to damped
Ly
systems at z =
2.5
(Prochaska et al. 2003a).
This sort of "missing metals" problem was first identified by
Pettini (1999)
for Lyman Break Galaxy SFRs compared to damped
Ly system metallicities,
but that problem could be solved by assuming that damped
Ly
system metallicities,
but that problem could be solved by assuming that damped
Ly systems are not the
descendants of the star-forming Lyman Break Galaxies. The damped
Ly
systems are not the
descendants of the star-forming Lyman Break Galaxies. The damped
Ly system "missing
metals" problem appears to be fundamental and may illuminate a
fundamental flaw in our understanding of the relationship between metal
enrichment and star formation at high redshift. The problem is a
significant challenge not only to the C II* method of measuring damped
Ly
system "missing
metals" problem appears to be fundamental and may illuminate a
fundamental flaw in our understanding of the relationship between metal
enrichment and star formation at high redshift. The problem is a
significant challenge not only to the C II* method of measuring damped
Ly SFRs, but to most
hierarchical models, which also produce too many metals (see
Nagamine, Springel &
Hernquist 2004b;
Somerville, Primack &
Faber 2001).
9 Given the other successes of the
method it seems likely that the problem has a physical solution.
SFRs, but to most
hierarchical models, which also produce too many metals (see
Nagamine, Springel &
Hernquist 2004b;
Somerville, Primack &
Faber 2001).
9 Given the other successes of the
method it seems likely that the problem has a physical solution.
The simplest solution would be to hypothesize that the damped
Ly systems forming stars
at z
systems forming stars
at z  2.5 are no
longer damped
Ly
2.5 are no
longer damped
Ly systems at z =
2.5 but have used up most of their neutral gas and now have the expected
metallicities; the Lyman Break Galaxies are an obvious candidate for
their descendants. This is inconsistent, however, with timescale of
systems at z =
2.5 but have used up most of their neutral gas and now have the expected
metallicities; the Lyman Break Galaxies are an obvious candidate for
their descendants. This is inconsistent, however, with timescale of
 2 Gyr to use up most
of the neutral gas implied by the observed SFRs, which is too
long. Ejecting the metals into the IGM does not solve the problem, as
the IGM metallicity predicted at z = 2.5 would be [M/H] = -1.5,
i.e., about a factor of 30 higher than that observed in the Lyman
2 Gyr to use up most
of the neutral gas implied by the observed SFRs, which is too
long. Ejecting the metals into the IGM does not solve the problem, as
the IGM metallicity predicted at z = 2.5 would be [M/H] = -1.5,
i.e., about a factor of 30 higher than that observed in the Lyman
 forest, unless the
ejected gas is so hot that most metals are in an unobservable ionization
state, with the possible exception of oxygen, which might be detected in
O VI
forest, unless the
ejected gas is so hot that most metals are in an unobservable ionization
state, with the possible exception of oxygen, which might be detected in
O VI 
 1031.9, 1037.6. An
alternative possibility is that the metals are sequestered, with the
most attractive solution being a model in which damped
Ly
1031.9, 1037.6. An
alternative possibility is that the metals are sequestered, with the
most attractive solution being a model in which damped
Ly systems represent
neutral gas on the outskirts of actively star-forming "bulge" regions
with the majority of the produced metals remaining in these regions
rather than polluting the damped
Ly
systems represent
neutral gas on the outskirts of actively star-forming "bulge" regions
with the majority of the produced metals remaining in these regions
rather than polluting the damped
Ly gas or general IGM
(Wolfe, Gawiser &
Prochaska 2003).
This hypothesis necessitates the conclusion that metal-rich bulge
regions are underrepresented (or completely unrepresented) in the H
I-weighted cosmic mean metallicity measured from DLAs. That would not be
surprising given that the bulges may well have used up most of their
neutral gas and/or have sufficient dust content to dim background QSOs
out of optically selected samples.
gas or general IGM
(Wolfe, Gawiser &
Prochaska 2003).
This hypothesis necessitates the conclusion that metal-rich bulge
regions are underrepresented (or completely unrepresented) in the H
I-weighted cosmic mean metallicity measured from DLAs. That would not be
surprising given that the bulges may well have used up most of their
neutral gas and/or have sufficient dust content to dim background QSOs
out of optically selected samples.
7 Due to its extreme
sensitivity to dust extinction,
Ly emission
provides a lower limit to the star formation rate as long as the AGN
contribution to the emission line is negligible.
Back.
emission
provides a lower limit to the star formation rate as long as the AGN
contribution to the emission line is negligible.
Back.
8 Note that Ap equals A(N, X) (see eq. 1) averaged over the column-density interval N(H I) = [Nmin, Nmax] Back.
9 The model of Pei et al.(1999) avoids this problem by invoking significant obscuration corrections and low yields. Back.