5. FRAGMENTATION OF THE FIRST GASEOUS OBJECTS TO STARS

5.1. Star Formation

As mentioned in the preface, the fragmentation of the first gaseous objects is a well-posed physics problem with well specified initial conditions, for a given power-spectrum of primordial density fluctuations. This problem is ideally suited for three-dimensional computer simulations, since it cannot be reliably addressed in idealized 1D or 2D geometries.

Recently, two groups have attempted detailed 3D simulations of the formation process of the first stars in a halo of ~ 10⁶ M by following the dynamics of both the dark matter and the gas components, including H₂ chemistry and cooling. Bromm, Coppi, & Larson (1999) [57] have used a Smooth Particle Hydrodynamics (SPH) code to simulate the collapse of a top-hat overdensity with a prescribed solid-body rotation (corresponding to a spin parameter = 5%) and additional small perturbations with P(k) k^-3 added to the top-hat profile. Abel et al. (2002) [5] isolated a high-density filament out of a larger simulated cosmological volume and followed the evolution of its density maximum with exceedingly high resolution using an Adaptive Mesh Refinement (AMR) algorithm.

Figure 20. Cooling rates as a function of temperature for a primordial gas composed of atomic hydrogen and helium, as well as molecular hydrogen, in the absence of any external radiation. We assume a hydrogen number density nH = 0.045 cm-3, corresponding to the mean density of virialized halos at z = 10. The plotted quantity / nH2 is roughly independent of density (unless nH > 10 cm-3), where is the volume cooling rate (in erg/sec/cm3). The solid line shows the cooling curve for an atomic gas, with the characteristic peaks due to collisional excitation of H1 and He2. The dashed line shows the additional contribution of molecular cooling, assuming a molecular abundance equal to 1% of nH.

The generic results of Bromm et al. (1999 [57]; see also Bromm 2000 [58]) are illustrated in Figure 21. The collapsing region forms a disk which fragments into many clumps. The clumps have a typical mass ~ 10² - 10³ M. This mass scale corresponds to the Jeans mass for a temperature of ~ 500K and the density ~ 10⁴ cm^-3 where the gas lingers because its cooling time is longer than its collapse time at that point (see Fig. 22). Each clump accretes mass slowly until it exceeds the Jeans mass and collapses at a roughly constant temperature (isothermally) due to H₂ cooling that brings the gas to a fixed temperature floor. The clump formation efficiency is high in this simulation due to the synchronized collapse of the overall top-hat perturbation.

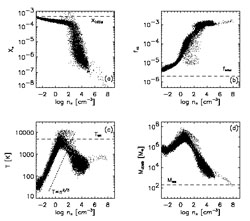Figure 21. Numerical results from Bromm et al. (1999) [57], showing gas properties at z = 31.2 for a collapsing slightly inhomogeneous top-hat region with a prescribed solid-body rotation. (a) Free electron fraction (by number) vs. hydrogen number density (in cm-3). At densities exceeding n ~ 103 cm-3, recombination is very efficient, and the gas becomes almost completely neutral. (b) Molecular hydrogen fraction vs. number density. After a quick initial rise, the H2 fraction approaches the asymptotic value of f ~ 10-3, due to the H- channel. (c) Gas temperature vs. number density. At densities below ~ 1 cm-3, the gas temperature rises because of adiabatic compression until it reaches the virial value of Tvir 5000 K. At higher densities, cooling due to H2 drives the temperature down again, until the gas settles into a quasi-hydrostatic state at T ~ 500 K and n ~ 104 cm-3. Upon further compression due to accretion and the onset of gravitational collapse, the gas shows a further modest rise in temperature. (d) Jeans mass (in M) vs. number density. The Jeans mass reaches a value of MJ ~ 103 M for the quasi-hydrostatic gas in the center of the potential well, and reaches the resolution limit of the simulation, Mres 200 M, for densities close to n = 108 cm-3.

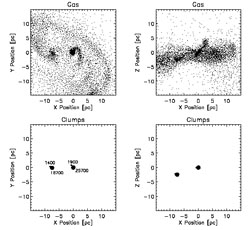Figure 22. Gas and clump morphology at z = 28.9 in the simulation of Bromm et al. (1999) [57]. Top row: The remaining gas in the diffuse phase. Bottom row: Distribution of clumps. The numbers next to the dots denote clump mass in units of M. Left panels: Face-on view. Right panels: Edge-on view. The length of the box is 30 pc. The gas has settled into a flattened configuration with two dominant clumps of mass close to 20,000 M. During the subsequent evolution, the clumps survive without merging, and grow in mass only slightly by accretion of surrounding gas.

Bromm (2000) [58] has simulated the collapse of one of the above-mentioned clumps with ~ 1000 M and demonstrated that it does not tend to fragment into sub-components. Rather, the clump core of ~ 100M free-falls towards the center leaving an extended envelope behind with a roughly isothermal density profile. At very high gas densities, three-body reactions become important in the chemistry of H₂. Omukai & Nishi (1998) [274] have included these reactions as well as radiative transfer and followed the collapse in spherical symmetry up to stellar densities. Radiation pressure from nuclear burning at the center is unlikely to reverse the infall as the stellar mass builds up. These calculations indicate that each clump may end as a single massive star; however, it is conceivable that angular momentum may eventually halt the collapsing cloud and lead to the formation of a binary stellar system instead.

The Jeans mass, which is defined based on small fluctuations in a background of uniform density, does not strictly apply in the context of collapsing gas cores. We can instead use a slightly modified critical mass known as the Bonnor-Ebert mass [53, 114]. For baryons in a background of uniform density _b, perturbations are unstable to gravitational collapse in a region more massive than the Jeans mass. Instead of a uniform background, we consider a spherical, non-singular, isothermal, self-gravitating gas in hydrostatic equilibrium, i.e., a centrally-concentrated object which more closely resembles the gas cores found in the above-mentioned simulations. In this case, small fluctuations are unstable and lead to collapse if the sphere is more massive than the Bonnor-Ebert mass M_BE, given by the same expression the Jeans Mass but with a different coefficient (1.2 instead of 2.9) and with _b denoting in this case the gas (volume) density at the surface of the sphere,

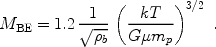(104)

In their simulation, Abel et al. (2000) [4] adopted the actual cosmological density perturbations as initial conditions. The simulation focused on the density peak of a filament within the IGM, and evolved it to very high densities (Fig. 23). Following the initial collapse of the filament, a clump core formed with ~ 200 M, amounting to only ~ 1% of the virialized mass. Subsequently due to slow cooling, the clump collapsed subsonically in a state close to hydrostatic equilibrium (see Fig. 24). Unlike the idealized top-hat simulation of Bromm et al. (2001) [59], the collapse of the different clumps within the filament is not synchronized. Once the first star forms at the center of the first collapsing clump, it is likely to affect the formation of other stars in its vicinity.

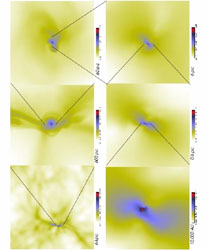Figure 23. Zooming in on the core of a star forming region with the Adaptive Mesh Refinement simulation of Abel et al. (2000) [4]. The panels show different length scales, decreasing clockwise by an order of magnitude between adjacent panels. Note the large dynamic range of scales which are being resolved, from 6 kpc (top left panel) down to 10,000 AU (bottom left panel).

As soon as nuclear burning sets in the core of the proto-star, the radiation emitted by the star starts to affect the infall of the surrounding gas towards it. The radiative feedback involves photo-dissociation of H₂, Ly radiation pressure, and photo-evaporation of the accretion disk. Tan & McKee [357] studied these effects by extrapolating analytically the infall of gas from the final snapshot of the above resolution-limited simulations to the scale of a proto-star; they concluded that nuclear burning (and hence the feedback) starts when the proton-star accretes ~ 30 M and accretion is likely to be terminated when the star reaches ~ 200 M.

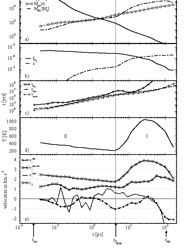Figure 24. Gas profiles from the simulation of Abel et al. (2000) [4]. The cell size on the finest grid corresponds to 0.024 pc, while the simulation box size corresponds to 6.4 kpc. Shown are spherically-averaged mass-weighted profiles around the baryon density peak shortly before a well defined fragment forms (z = 19.1). Panel (a) shows the baryonic number density, enclosed gas mass in solar mass, and the local Bonnor-Ebert mass MBE (see text). Panel (b) plots the molecular hydrogen fraction (by number) fH2 and the free electron fraction x. The H2 cooling time, tH2, the time it takes a sound wave to travel to the center, tcross, and the free - fall time tff = [3 / (32G )]1/2 are given in panel (c). Panel (d) gives the temperature in K as a function of radius. The bottom panel gives the local sound speed, cs (solid line with circles), the rms radial velocities of the dark matter (dashed line) and the gas (dashed line with asterisks) as well as the rms gas velocity (solid line with square symbols). The vertical dotted line indicates the radius (~ 5 pc) at which the gas has reached its minimum temperature allowed by H2 cooling. The virial radius of the 5.6 × 106 M halo is 106 pc.

If the clumps in the above simulations end up forming individual very massive stars, then these stars will likely radiate copious amounts of ionizing radiation [50, 370, 59] and expel strong winds. Hence, the stars will have a large effect on their interstellar environment, and feedback is likely to control the overall star formation efficiency. This efficiency is likely to be small in galactic potential wells which have a virial temperature lower than the temperature of photoionized gas, ~ 10⁴K. In such potential wells, the gas may go through only a single generation of star formation, leading to a "suicidal" population of massive stars.

The final state in the evolution of these stars is uncertain; but if their mass loss is not too extensive, then they are likely to end up as black holes [50, 137]. The remnants may provide the seeds of quasar black holes [215]. Some of the massive stars may end their lives by producing gamma-ray bursts. If so then the broad-band afterglows of these bursts could provide a powerful tool for probing the epoch of reionization [214, 94]). There is no better way to end the dark ages than with -ray burst fireworks.

Where are the first stars or their remnants located today? The very first stars formed in rare high- peaks and hence are likely to populate the cores of present-day galaxies [380]. However, the bulk of the stars which formed in low-mass systems at later times are expected to behave similarly to the collisionless dark matter particles and populate galaxy halos [221].

5.2. The Mass Function of Stars

Currently, we do not have direct observational constraints on how the first stars, the so-called Population III stars, formed at the end of the cosmic dark ages. It is, therefore, instructive to briefly summarize what we have learned about star formation in the present-day Universe, where theoretical reasoning is guided by a wealth of observational data (see [293] for a recent review).

Population I stars form out of cold, dense molecular gas that is structured in a complex, highly inhomogeneous way. The molecular clouds are supported against gravity by turbulent velocity fields and pervaded on large scales by magnetic fields. Stars tend to form in clusters, ranging from a few hundred up to ~ 10⁶ stars. It appears likely that the clustered nature of star formation leads to complicated dynamics and tidal interactions that transport angular momentum, thus allowing the collapsing gas to overcome the classical centrifugal barrier [216]. The initial mass function (IMF) of Pop I stars is observed to have the approximate Salpeter form (e.g., [208])

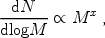(105)

where

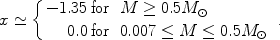(106)

The lower cutoff in mass corresponds roughly to the opacity limit for fragmentation. This limit reflects the minimum fragment mass, set when the rate at which gravitational energy is released during the collapse exceeds the rate at which the gas can cool (e.g., [298]). The most important feature of the observed IMF is that ~ 1 M is the characteristic mass scale of Pop I star formation, in the sense that most of the mass goes into stars with masses close to this value. In Figure 25, we show the result from a recent hydrodynamical simulation of the collapse and fragmentation of a molecular cloud core [31, 32]. This simulation illustrates the highly dynamic and chaotic nature of the star formation process ⁶.

Figure 25. A hydrodynamic simulation of the collapse and fragmentation of a turbulent molecular cloud in the present-day Universe (from [32]). The cloud has a mass of 50 M. The panels show the column density through the cloud, and span a scale of 0.4 pc across. Left: The initial phase of the collapse. The turbulence organizes the gas into a network of filaments, and decays thereafter through shocks. Right: A snapshot taken near the end of the simulation, after 1.4 initial free-fall times of 2 × 105yr. Fragmentation has resulted in ~ 50 stars and brown dwarfs. The star formation efficiency is ~ 10% on the scale of the overall cloud, but can be much larger in the dense sub-condensations. This result is in good agreement with what is observed in local star-forming regions.

Bromm & Loeb (2004) [67] carried out idealized simulations of the protostellar accretion problem and estimated the final mass of a Population III star. Using the smoothed particle hydrodynamics (SPH) method, they included the chemistry and cooling physics relevant for the evolution of metal-free gas (see [62] for details). Improving on earlier work [57, 62] by initializing the simulations according to the CDM model, they focused on an isolated overdense region that corresponds to a 3-peak [67]: a halo containing a total mass of 10⁶ M, and collapsing at a redshift z_vir 20. In these runs, one high-density clump has formed at the center of the minihalo, possessing a gas mass of a few hundred solar masses. Soon after its formation, the clump becomes gravitationally unstable and undergoes runaway collapse. Once the gas clump has exceeded a threshold density of 10⁷ cm^-3, it is replaced by a sink particle which is a collisionless point-like particle that is inserted into the simulation. This choice for the density threshold ensures that the local Jeans mass is resolved throughout the simulation. The clump (i.e., sink particle) has an initial mass of M_Cl 200M, and grows subsequently by ongoing accretion of surrounding gas. High-density clumps with such masses result from the chemistry and cooling rate of molecular hydrogen, H₂, which imprint characteristic values of temperature, T ~ 200 K, and density, n ~ 10⁴ cm^-3, into the metal-free gas [62]. Evaluating the Jeans mass for these characteristic values results in M_J ~ a few × 10² M, which is close to the initial clump masses found in the simulations.

The high-density clumps are clearly not stars yet. To probe the subsequent fate of a clump, Bromm & Loeb (2004) [67] have re-simulated the evolution of the central clump with sufficient resolution to follow the collapse to higher densities. Figure 26 (right panel) shows the gas density on a scale of 0.5 pc, which is two orders of magnitude smaller than before. Several features are evident in this plot. First, the central clump does not undergo further sub-fragmentation, and is likely to form a single Population III star. Second, a companion clump is visible at a distance of ~ 0.25 pc. If negative feedback from the first-forming star is ignored, this companion clump would undergo runaway collapse on its own approximately ~ 3 Myr later. This timescale is comparable to the lifetime of a very massive star (VMS) [59]. If the second clump was able to survive the intense radiative heating from its neighbor, it could become a star before the first one explodes as a supernova (SN). Whether more than one star can form in a low-mass halo thus crucially depends on the degree of synchronization of clump formation. Finally, the non-axisymmetric disturbance induced by the companion clump, as well as the angular momentum stored in the orbital motion of the binary system, allow the system to overcome the angular momentum barrier for the collapse of the central clump (see [216]).

Figure 26. Collapse and fragmentation of a primordial cloud (from [67]). Shown is the projected gas density at a redshift z 21.5, briefly after gravitational runaway collapse has commenced in the center of the cloud. Left: The coarse-grained morphology in a box with linear physical size of 23.5 pc. At this time in the unrefined simulation, a high-density clump (sink particle) has formed with an initial mass of ~ 103 M. Right: The refined morphology in a box with linear physical size of 0.5 pc. The central density peak, vigorously gaining mass by accretion, is accompanied by a secondary clump.

The recent discovery of stars like HE0107-5240 with a mass of 0.8 M and an iron abundance of [Fe/H] = -5.3 [90] shows that at least some low mass stars could have formed out of extremely low-metallicity gas. The above simulations show that although the majority of clumps are very massive, a few of them, like the secondary clump in Fig. 26, are significantly less massive. Alternatively, low-mass fragments could form in the dense, shock-compressed shells that surround the first hypernovae [234].

How massive were the first stars? Star formation typically proceeds from the `inside-out', through the accretion of gas onto a central hydrostatic core. Whereas the initial mass of the hydrostatic core is very similar for primordial and present-day star formation [274], the accretion process - ultimately responsible for setting the final stellar mass, is expected to be rather different. On dimensional grounds, the accretion rate is simply related to the sound speed cubed over Newton's constant (or equivalently given by the ratio of the Jeans mass and the free-fall time): M_acc ~ c_s³ / G T^3/2. A simple comparison of the temperatures in present-day star forming regions (T ~ 10 K) with those in primordial ones (T ~ 200-300 K) already indicates a difference in the accretion rate of more than two orders of magnitude.

The above refined simulation enables one to study the three-dimensional accretion flow around the protostar (see also [276, 304, 357]). The gas may now reach densities of 10¹² cm^-3 before being incorporated into a central sink particle. At these high densities, three-body reactions [280] convert the gas into a fully molecular form. Figure 27 shows how the molecular core grows in mass over the first ~ 10⁴ yr after its formation. The accretion rate (left panel) is initially very high, M_acc ~ 0.1 M yr^-1, and subsequently declines according to a power law, with a possible break at ~ 5000 yr. The mass of the molecular core (right panel), taken as an estimator of the proto-stellar mass, grows approximately as: M_* ~ _acc dt t^0.45. A rough upper limit for the final mass of the star is then: M_*(t = 3 × 10⁶ yr) ~ 700 M. In deriving this upper bound, we have conservatively assumed that accretion cannot go on for longer than the total lifetime of a massive star.

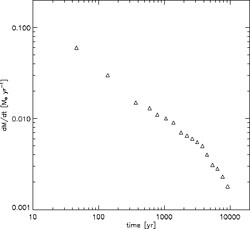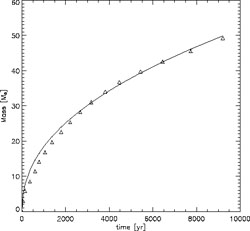Figure 27. Accretion onto a primordial protostar (from [67]). The morphology of this accretion flow is shown in Fig. 26. Left: Accretion rate (in M yr-1) vs. time (in yr) since molecular core formation. Right: Mass of the central core (in M) vs. time. Solid line: Accretion history approximated as: M* t0.45. Using this analytical approximation, we extrapolate that the protostellar mass has grown to ~ 150 M after ~ 105 yr, and to ~ 700 M after ~ 3 × 106 yr, the total lifetime of a very massive star.

Can a Population III star ever reach this asymptotic mass limit? The answer to this question is not yet known with any certainty, and it depends on whether the accretion from a dust-free envelope is eventually terminated by feedback from the star (e.g., [276, 304, 357, 277]). The standard mechanism by which accretion may be terminated in metal-rich gas, namely radiation pressure on dust grains [386], is evidently not effective for gas with a primordial composition. Recently, it has been speculated that accretion could instead be turned off through the formation of an H II region [277], or through the photo-evaporation of the accretion disk [357]. The termination of the accretion process defines the current unsolved frontier in studies of Population III star formation. Current simulations indicate that the first stars were predominantly very massive (> 30 M), and consequently rather different from present-day stellar populations. The crucial question then arises: How and when did the transition take place from the early formation of massive stars to that of low-mass stars at later times? We address this problem next.

The very first stars, marking the cosmic Renaissance of structure formation, formed under conditions that were much simpler than the highly complex environment in present-day molecular clouds. Subsequently, however, the situation rapidly became more complicated again due to the feedback from the first stars on the IGM. Supernova explosions dispersed the nucleosynthetic products from the first generation of stars into the surrounding gas (e.g., [241, 261, 361]), including also dust grains produced in the explosion itself [222, 364]. Atomic and molecular cooling became much more efficient after the addition of these metals. Moreover, the presence of ionizing cosmic rays, as well as of UV and X-ray background photons, modified the thermal and chemical behavior of the gas in important ways (e.g., [232, 233]).

Early metal enrichment was likely the dominant effect that brought about the transition from Population III to Population II star formation. Recent numerical simulations of collapsing primordial objects with overall masses of ~ 10⁶ M, have shown that the gas has to be enriched with heavy elements to a minimum level of Z_crit 10^-3.5 Z, in order to have any effect on the dynamics and fragmentation properties of the system [275, 60, 64]. Normal, low-mass (Population II) stars are hypothesized to only form out of gas with metallicity Z Z_crit. Thus, the characteristic mass scale for star formation is expected to be a function of metallicity, with a discontinuity at Z_crit where the mass scale changes by ~ two orders of magnitude. The redshift where this transition occurs has important implications for the early growth of cosmic structure, and the resulting observational signature (e.g., [392, 141, 234, 322]) include the extended nature of reionization [144].

For additional detailes about the properties of the first stars, see the comprehensive review by Bromm & Larson (2004) [66].

5.3. Gamma-ray Bursts: Probing the First Stars One Star at a Time

Gamma-Ray Bursts (GRBs) are believed to originate in compact remnants (neutron stars or black holes) of massive stars. Their high luminosities make them detectable out to the edge of the visible Universe [94, 214]. GRBs offer the opportunity to detect the most distant (and hence earliest) population of massive stars, the so-called Population III (or Pop III), one star at a time. In the hierarchical assembly process of halos which are dominated by cold dark matter (CDM), the first galaxies should have had lower masses (and lower stellar luminosities) than their low-redshift counterparts. Consequently, the characteristic luminosity of galaxies or quasars is expected to decline with increasing redshift. GRB afterglows, which already produce a peak flux comparable to that of quasars or starburst galaxies at z ~ 1-2, are therefore expected to outshine any competing source at the highest redshifts, when the first dwarf galaxies have formed in the Universe.

Figure 28. Illustration of a long-duration gamma-ray burst in the popular "collapsar" model. The collapse of the core of a massive star (which lost its hydrogen envelope) to a black hole generates two opposite jets moving out at a speed close to the speed of light. The jets drill a hole in the star and shine brightly towards an observer who happened to be located within with the collimation cones of the jets. The jets emenating from a single massive star are so bright that they can be seen across the Universe out to the epoch when the first stars have formed. Upcoming observations by the Swift satellite will have the sensitivity to reveal whether the first stars served as progenitors of gamma-ray bursts (for updates see http://swift.gsfc.nasa.gov/).

The first-year polarization data from the Wilkinson Microwave Anisotropy Probe (WMAP) indicates an optical depth to electron scattering of ~ 17 ± 4% after cosmological recombination [203, 348]. This implies that the first stars must have formed at a redshift z ~ 10 - 20, and reionized a substantial fraction of the intergalactic hydrogen around that time [83, 93, 345, 394, 403]. Early reionization can be achieved with plausible star formation parameters in the standard CDM cosmology; in fact, the required optical depth can be achieved in a variety of very different ionization histories since WMAP places only an integral constraint on these histories [176]. One would like to probe the full history of reionization in order to disentangle the properties and formation history of the stars that are responsible for it. GRB afterglows offer the opportunity to detect stars as well as to probe the metal enrichment level [141] of the intervening IGM.

GRBs, the electromagnetically-brightest explosions in the Universe, should be detectable out to redshifts z > 10 [94, 214]. High-redshift GRBs can be identified through infrared photometry, based on the Ly break induced by absorption of their spectrum at wavelengths below 1.216 µm [(1 + z) / 10]. Follow-up spectroscopy of high-redshift candidates can then be performed on a 10-meter-class telescope. Recently, the ongoing Swift mission [147] has detected a GRB originating at z 6.3 (e.g., [179]), thus demonstrating the viability of GRBs as probes of the early Universe.

There are four main advantages of GRBs relative to traditional cosmic sources such as quasars:

(i) The GRB afterglow flux at a given observed time lag after the -ray trigger is not expected to fade significantly with increasing redshift, since higher redshifts translate to earlier times in the source frame, during which the afterglow is intrinsically brighter [94]. For standard afterglow lightcurves and spectra, the increase in the luminosity distance with redshift is compensated by this cosmological time-stretching effect.

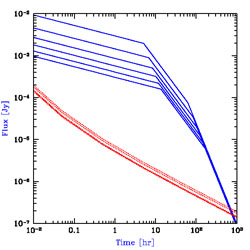Figure 29. GRB afterglow flux as a function of time since the -ray trigger in the observer frame (taken from [67]). The flux (solid curves) is calculated at the redshifted Ly wavelength. The dotted curves show the planned detection threshold for the James Webb Space Telescope (JWST), assuming a spectral resolution R = 5000 with the near infrared spectrometer, a signal to noise ratio of 5 per spectral resolution element, and an exposure time equal to 20% of the time since the GRB explosion (see http://www.ngst.stsci.edu/nms/main/). Each set of curves shows a sequence of redshifts, namely z = 5, 7, 9, 11, 13, and 15, respectively, from top to bottom.

(ii) As already mentioned, in the standard CDM cosmology, galaxies form hierarchically, starting from small masses and increasing their average mass with cosmic time. Hence, the characteristic mass of quasar black holes and the total stellar mass of a galaxy were smaller at higher redshifts, making these sources intrinsically fainter [391]. However, GRBs are believed to originate from a stellar mass progenitor and so the intrinsic luminosity of their engine should not depend on the mass of their host galaxy. GRB afterglows are therefore expected to outshine their host galaxies by a factor that gets larger with increasing redshift.

(iii) Since the progenitors of GRBs are believed to be stellar, they likely originate in the most common star-forming galaxies at a given redshift rather than in the most massive host galaxies, as is the case for bright quasars [26]. Low-mass host galaxies induce only a weak ionization effect on the surrounding IGM and do not greatly perturb the Hubble flow around them. Hence, the Ly damping wing should be closer to the idealized unperturbed IGM case and its detailed spectral shape should be easier to interpret. Note also that unlike the case of a quasar, a GRB afterglow can itself ionize at most ~ 4 × 10⁴ E₅₁ M of hydrogen if its UV energy is E₅₁ in units of 10⁵¹ ergs (based on the available number of ionizing photons), and so it should have a negligible cosmic effect on the surrounding IGM.

(iv) GRB afterglows have smooth (broken power-law) continuum spectra unlike quasars which show strong spectral features (such as broad emission lines or the so-called "blue bump") that complicate the extraction of IGM absorption features. In particular, the continuum extrapolation into the Ly damping wing (the so-called Gunn-Peterson absorption trough) during the epoch of reionization is much more straightforward for the smooth UV spectra of GRB afterglows than for quasars with an underlying broad Ly emission line [26].

The optical depth of the uniform IGM to Ly absorption is given by (Gunn & Peterson 1965 [163]),

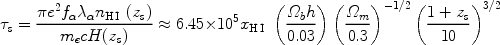(107)

where H 100h km s^-1 Mpc^-1 _m^1/2(1 + z_s)^3/2 is the Hubble parameter at the source redshift z_s >> 1, f = 0.4162 and = 1216 Å are the oscillator strength and the wavelength of the Ly transition; n_HI(z_s) is the neutral hydrogen density at the source redshift (assuming primordial abundances); _m and _b are the present-day density parameters of all matter and of baryons, respectively; and x_HI is the average fraction of neutral hydrogen. In the second equality we have implicitly considered high-redshifts, (1 + z) >> max[(1 - _m - ) / _m, ( / _m)^1/3], at which the vacuum energy density is negligible relative to matter ( << _m) and the Universe is nearly flat; for _m = 0.3, = 0.7 this corresponds to the condition z >> 1.3 which is well satisfied by the reionization redshift.

At wavelengths longer than Ly at the source, the optical depth obtains a small value; these photons redshift away from the line center along its red wing and never resonate with the line core on their way to the observer. The red damping wing of the Gunn-Peterson trough (Miralda-Escudé 1998 [254])

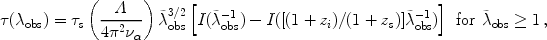(108)

where _s is given in equation (107), also we define

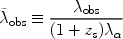(109)

and

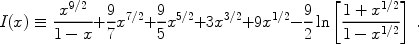(110)

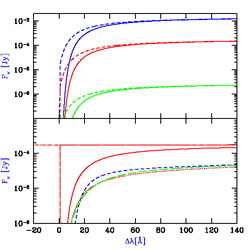Figure 30. Expected spectral shape of the Ly absorption trough due to intergalactic absorption in GRB afterglows (taken from [67]). The spectrum is presented in terms of the flux density F versus relative observed wavelength , for a source redshift z = 7 (assumed to be prior to the final reionization phase) and the typical halo mass M = 4 × 108 M expected for GRB host galaxies that cool via atomic transitions. Top panel: Two examples for the predicted spectrum including IGM HI absorption (both resonant and damping wing), for host galaxies with (i) an age ts = 107 yr, a UV escape fraction fesc = 10% and a Scalo initial mass function (IMF) in solid curves, or (ii) ts = 108 yr, fesc = 90% and massive (> 100 M) Pop III stars in dashed curves. The observed time after the -ray trigger is one hour, one day, and ten days, from top to bottom, respectively. Bottom panel: Predicted spectra one day after a GRB for a host galaxy with ts = 107 yr, fesc = 10% and a Scalo IMF. Shown is the unabsorbed GRB afterglow (dot-short dashed curve), the afterglow with resonant IGM absorption only (dot-long dashed curve), and the afterglow with full (resonant and damping wing) IGM absorption (solid curve). Also shown, with 1.7 magnitudes of extinction, are the afterglow with full IGM absorption (dotted curve), and attempts to reproduce this profile with a damped Ly absorption system in the host galaxy (dashed curves). (Note, however, that damped absorption of this type could be suppressed by the ionizing effect of the afterglow UV radiation on the surrounding interstellar medium of its host galaxy [289].) Most importantly, the overall spectral shape of the Ly trough carries precious information about the neutral fraction of the IGM at the source redshift; averaging over an ensemble of sources with similar redshifts can reduce ambiguities in the interpretation of each case due to particular local effects.

Although the nature of the central engine that powers the relativistic jets of GRBs is still unknown, recent evidence indicates that long-duration GRBs trace the formation of massive stars (e.g., [365, 383, 45, 211, 47, 264]) and in particular that long-duration GRBs are associated with Type Ib/c supernovae [351]. Since the first stars in the Universe are predicted to be predominantly massive [5, 62, 66], their death might give rise to large numbers of GRBs at high redshifts. In contrast to quasars of comparable brightness, GRB afterglows are short-lived and release ~ 10 orders of magnitude less energy into the surrounding IGM. Beyond the scale of their host galaxy, they have a negligible effect on their cosmological environment ⁷. Consequently, they are ideal probes of the IGM during the reionization epoch. Their rest-frame UV spectra can be used to probe the ionization state of the IGM through the spectral shape of the Gunn-Peterson (Ly) absorption trough, or its metal enrichment history through the intersection of enriched bubbles of supernova (SN) ejecta from early galaxies [141]. Afterglows that are unusually bright (> 10 mJy) at radio frequencies should also show a detectable forest of 21 cm absorption lines due to enhanced HI column densities in sheets, filaments, and collapsed minihalos within the IGM [76, 140].

Another advantage of GRB afterglows is that once they fade away, one may search for their host galaxies. Hence, GRBs may serve as signposts of the earliest dwarf galaxies that are otherwise too faint or rare on their own for a dedicated search to find them. Detection of metal absorption lines from the host galaxy in the afterglow spectrum, offers an unusual opportunity to study the physical conditions (temperature, metallicity, ionization state, and kinematics) in the interstellar medium of these high-redshift galaxies. As Figure 30 indicates, damped Ly absorption within the host galaxy may mask the clear signature of the Gunn-Peterson trough in some galaxies [67]. A small fraction ( ~ 10) of the GRB afterglows are expected to originate at redshifts z > 5 [61, 68]. This subset of afterglows can be selected photometrically using a small telescope, based on the Ly break at a wavelength of 1.216 µm< [(1 + z) / 10], caused by intergalactic HI absorption. The challenge in the upcoming years will be to follow-up on these candidates spectroscopically, using a large (10-meter class) telescope. GRB afterglows are likely to revolutionize observational cosmology and replace traditional sources like quasars, as probes of the IGM at z > 5. The near future promises to be exciting for GRB astronomy as well as for studies of the high-redshift Universe.

It is of great importance to constrain the Pop III star formation mode, and in particular to determine down to which redshift it continues to be prominent. The extent of the Pop III star formation will affect models of the initial stages of reionization (e.g., [394, 93, 343, 403, 12]) and metal enrichment (e.g., [234, 141, 144, 320, 340]), and will determine whether planned surveys will be able to effectively probe Pop III stars (e.g., [319]). The constraints on Pop III star formation will also determine whether the first stars could have contributed a significant fraction to the cosmic near-IR background (e.g., [311, 310, 193, 242, 113]). To constrain high-redshift star formation from GRB observations, one has to address two major questions:

(1) What is the signature of GRBs that originate in metal-free, Pop III progenitors? Simply knowing that a given GRB came from a high redshift is not sufficient to reach a definite conclusion as to the nature of the progenitor. Pregalactic metal enrichment was likely inhomogeneous, and we expect normal Pop I and II stars to exist in galaxies that were already metal-enriched at these high redshifts [68]. Pop III and Pop I/II star formation is thus predicted to have occurred concurrently at z > 5. How is the predicted high mass-scale for Pop III stars reflected in the observational signature of the resulting GRBs? Preliminary results from numerical simulations of Pop III star formation indicate that circumburst densities are systematically higher in Pop III environments. GRB afterglows will then be much brighter than for conventional GRBs. In addition, due to the systematically increased progenitor masses, the Pop III distribution may be biased toward long-duration events.

(2) The modelling of Pop III cosmic star formation histories has a number of free parameters, such as the star formation efficiency and the strength of the chemical feedback. The latter refers to the timescale for, and spatial extent of, the distribution of the first heavy elements that were produced inside of Pop III stars, and subsequently dispersed into the IGM by supernova blast waves. Comparing with theoretical GRB redshift distributions one can use the GRB redshift distribution observed by Swift to calibrate the free model parameters. In particular, one can use this strategy to measure the redshift where Pop III star formation terminates.

Figures 31 and 32 illustrate these issues (based on [68]). Figure 32 leads to the robust expectation that ~ 10% of all Swift bursts should originate at z > 5. This prediction is based on the contribution from Population I/II stars which are known to exist even at these high redshifts. Additional GRBs could be triggered by Pop III stars, with a highly uncertain efficiency. Assuming that long-duration GRBs are produced by the collapsar mechanism, a Pop III star with a close binary companion provides a plausible GRB progenitor. The Pop III GRB efficiency, reflecting the probability of forming sufficiently close and massive binary systems, to lie between zero (if tight Pop III binaries do not exist) and ~ 10 times the empirically inferred value for Population I/II (due to the increased fraction of black hole forming progenitors among the massive Pop III stars).

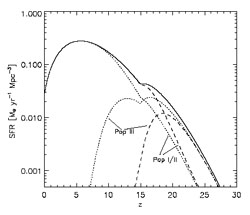Figure 31. Theoretical prediction for the comoving star formation rate (SFR) in units of M yr-1 Mpc-3, as a function of redshift (from [68]). We assume that cooling in primordial gas is due to atomic hydrogen only, a star formation efficiency of * = 10%, and reionization beginning at zreion 17. Solid line: Total comoving SFR. Dotted lines: Contribution to the total SFR from Pop I/II and Pop III for the case of weak chemical feedback. Dashed lines: Contribution to the total SFR from Pop I/II and Pop III for the case of strong chemical feedback. Pop III star formation is restricted to high redshifts, but extends over a significant range, z ~ 10-15.

A key ingredient in determining the underlying star formation history from the observed GRB redshift distribution is the GRB luminosity function, which is only poorly constrained at present. The improved statistics provided by Swift will enable the construction of an empirical luminosity function. With an improved luminosity function it would be possible to re-calibrate the theoretical prediction in Figure 32 more reliably.

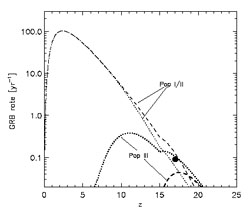Figure 32. Predicted GRB rate to be observed by Swift (from [68]). Shown is the observed number of bursts per year, dNGRBobs / dln(1 + z), as a function of redshift. All rates are calculated with a constant GRB efficiency, GRB 2 × 10-9 bursts M-1, using the cosmic SFRs from Fig. 31. Dotted lines: Contribution to the observed GRB rate from Pop I/II and Pop III for the case of weak chemical feedback. Dashed lines: Contribution to the GRB rate from Pop I/II and Pop III for the case of strong chemical feedback. Filled circle: GRB rate from Pop III stars if these were responsible for reionizing the Universe at z ~ 17.

In order to predict the observational signature of high-redshift GRBs, it is important to know the properties of the GRB host systems. Within variants of the popular CDM model for structure formation, where small objects form first and subsequently merge to build up more massive ones, the first stars are predicted to form at z ~ 20 - 30 in minihalos of total mass (dark matter plus gas) ~ 10⁶ M [359, 23, 403]. These objects are the sites for the formation of the first stars, and thus are the potential hosts of the highest-redshift GRBs. What is the environment in which the earliest GRBs and their afterglows did occur? This problem breaks down into two related questions: (i) what type of stars (in terms of mass, metallicity, and clustering properties) will form in each minihalo?, and (ii) how will the ionizing radiation from each star modify the density structure of the surrounding gas? These two questions are fundamentally intertwined. The ionizing photon production strongly depends on the stellar mass, which in turn is determined by how the accretion flow onto the growing protostar proceeds under the influence of this radiation field. In other words, the assembly of the Population III stars and the development of an HII region around them proceed simultaneously, and affect each other. As a preliminary illustration, Figure 27 describes the photo-evaporation as a self-similar champagne flow [337] with parameters appropriate for the Pop III case.

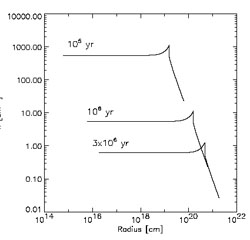Figure 33. Effect of photoheating from a Population III star on the density profile in a high-redshift minihalo (from [69]). The curves, labeled by the time after the onset of the central point source, are calculated according to a self-similar model for the expansion of an HII region. Numerical simulations closely conform to this analytical behavior. Notice that the central density is significantly reduced by the end of the life of a massive star, and that a central core has developed where the density is constant.

Notice that the central density is significantly reduced by the end of the life of a massive star, and that a central core has developed where the density is nearly constant. Such a flat density profile is markedly different from that created by stellar winds ( r^-2). Winds, and consequently mass-loss, may not be important for massive Population III stars [18, 210], and such a flat density profile may be characteristic of GRBs that originate from metal-free Population III progenitors.

The first galaxies may be surrounded by a shell of highly enriched material that was carried out in a SN-driven wind (see Fig. 34). A GRB in that galaxy may show strong absorption lines at a velocity separation associated with the wind velocity. Simulating these winds and calculating the absorption profile in the featureless spectrum of a GRB afterglow, will allow us to use the observed spectra of high-z GRBs and directly probe the degree of metal enrichment in the vicinity of the first star forming regions (see [141] for a semi-analytic treatment).

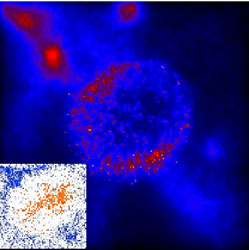Figure 34. Supernova explosion in the high-redshift Universe (from [65]). The snapshot is taken ~ 106 yr after the explosion with total energy ESN 1053 ergs. We show the projected gas density within a box of linear size 1 kpc. The SN bubble has expanded to a radius of ~ 200 pc, having evacuated most of the gas in the minihalo. Inset: Distribution of metals. The stellar ejecta (gray dots) trace the metals and are embedded in pristine metal-poor gas (black dots).

As the early afterglow radiation propagates through the interstellar environment of the GRB, it will likely modify the gas properties close to the source; these changes could in turn be noticed as time-dependent spectral features in the spectrum of the afterglow and used to derive the properties of the gas cloud (density, metal abundance, and size). The UV afterglow radiation can induce detectable changes to the interstellar absorption features of the host galaxy [289]; dust destruction could have occurred due to the GRB X-rays [375, 136], and molecules could have been destroyed near the GRB source [112]. Quantitatively, all of the effects mentioned above strongly depend on the exact properties of the gas in the host system.

Most studies to date have assumed a constant efficiency of forming GRBs per unit mass of stars. This simplifying assumption could lead, under different circumstances, to an overestimation or an underestimation of the frequency of GRBs. Metal-free stars are thought to be massive [5, 62] and their extended envelopes may suppress the emergence of relativistic jets out of their surface (even if such jets are produced through the collapse of their core to a spinning black hole). On the other hand, low-metallicity stars are expected to have weak winds with little angular momentum loss during their evolution, and so they may preferentially yield rotating central configurations that make GRB jets after core collapse.

What kind of metal-free, Pop III progenitor stars may lead to GRBs? Long-duration GRBs appear to be associated with Type Ib/c supernovae [351], namely progenitor massive stars that have lost their hydrogen envelope. This requirement is explained theoretically in the collapsar model, in which the relativistic jets produced by core collapse to a black hole are unable to emerge relativistically out of the stellar surface if the hydrogen envelope is retained [231]. The question then arises as to whether the lack of metal line-opacity that is essential for radiation-driven winds in metal-rich stars, would make a Pop III star retain its hydrogen envelope, thus quenching any relativistic jets and GRBs.

Aside from mass transfer in a binary system, individual PopIII stars could lose their hydrogen envelope due to either: (i) violent pulsations, particularly in the mass range 100 - 140 M, or (ii) a wind driven by helium lines. The outer stellar layers are in a state where gravity only marginally exceeds radiation pressure due to electron-scattering (Thomson) opacity. Adding the small, but still non-negligible contribution from the bound-free opacity provided by singly-ionized helium, may be able to unbind the atmospheric gas. Therefore, mass-loss might occur even in the absence of dust or any heavy elements.

5.4. Emission Spectrum of Metal-Free Stars

The evolution of metal-free (Population III) stars is qualitatively different from that of enriched (Population I and II) stars. In the absence of the catalysts necessary for the operation of the CNO cycle, nuclear burning does not proceed in the standard way. At first, hydrogen burning can only occur via the inefficient PP chain. To provide the necessary luminosity, the star has to reach very high central temperatures (T_c 10^8.1 K). These temperatures are high enough for the spontaneous turn-on of helium burning via the triple- process. After a brief initial period of triple- burning, a trace amount of heavy elements forms. Subsequently, the star follows the CNO cycle. In constructing main-sequence models, it is customary to assume that a trace mass fraction of metals (Z ~ 10^-9) is already present in the star (El Eid 1983 [115]; Castellani et al. 1983 [78]).

Figures 35 and 36 show the luminosity L vs. effective temperature T for zero-age main sequence stars in the mass ranges of 2 - 90 M (Fig. 35) and 100 - 1000 M (Fig. 36). Note that above ~ 100M the effective temperature is roughly constant, T_eff ~ 10⁵ K, implying that the spectrum is independent of the mass distribution of the stars in this regime (Bromm, Kudritzky, & Loeb 2001 [59]). As is evident from these figures (see also Tumlinson & Shull 2000 [370]), both the effective temperature and the ionizing power of metal-free (Pop III) stars are substantially larger than those of metal-rich (Pop I) stars. Metal-free stars with masses > 20M emit between 10⁴⁷ and 10⁴⁸ H I and He I ionizing photons per second per solar mass of stars, where the lower value applies to stars of ~ 20 M and the upper value applies to stars of > 100 M (see Tumlinson & Shull 2000 [370] and Bromm et al. 2001 [59] for more details). Over a lifetime of ~ 3 × 10⁶ years these massive stars produce 10⁴ - 10⁵ ionizing photons per stellar baryon. However, this powerful UV emission is suppressed as soon as the interstellar medium out of which new stars form is enriched by trace amounts of metals. Even though the collapsed fraction of baryons is small at the epoch of reionization, it is likely that most of the stars responsible for the reionization of the Universe formed out of enriched gas.

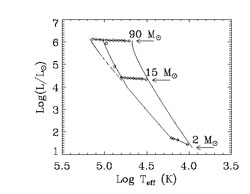Figure 35. Luminosity vs. effective temperature for zero-age main sequences stars in the mass range of 2 - 90M (from Tumlinson & Shull 2000 [370]). The curves show Pop I (Z = 0.02) and Pop III stars of mass 2, 5, 8, 10, 15, 20, 25, 30, 35, 40, 50, 60, 70, 80, and 90 M. The diamonds mark decades in metallicity in the approach to Z = 0 from 10-2 down to 10-5 at 2 M, down to 10-10 at 15 M, and down to 10-13 at 90 M. The dashed line along the Pop III ZAMS assumes pure H-He composition, while the solid line (on the left) marks the upper MS with Zc = 10-10 for the M 15 M models. Squares mark the points corresponding to pre-enriched evolutionary models from El Eid et al. (1983) [115] at 80 M and from Castellani et al. (1983) [78] for 25 M.

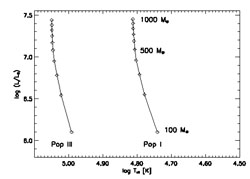Figure 36. Same as Figure 35 but for very massive stars above 100M (from Bromm, Kudritzki, & Loeb 2001 [59]). Left solid line: Pop III zero-age main sequence (ZAMS). Right solid line: Pop I ZAMS. In each case, stellar luminosity (in L) is plotted vs. effective temperature (in K). Diamond-shaped symbols: Stellar masses along the sequence, from 100 M (bottom) to 1000 M (top) in increments of 100 M. The Pop III ZAMS is systematically shifted to higher effective temperature, with a value of ~ 105 K which is approximately independent of mass. The luminosities, on the other hand, are almost identical in the two cases.

Will it be possible to infer the initial mass function (IMF) of the first stars from spectroscopic observations of the first galaxies? Figure 37 compares the observed spectrum from a Salpeter IMF (dN_* / dM M^-2.35) and a heavy IMF (with all stars more massive than 100 M) for a galaxy at z_s = 10. The latter case follows from the assumption that each of the dense clumps in the simulations described in the previous section ends up as a single star with no significant fragmentation or mass loss. The difference between the plotted spectra cannot be confused with simple reddening due to normal dust. Another distinguishing feature of the IMF is the expected flux in the hydrogen and helium recombination lines, such as Ly and He II 1640 Å, from the interstellar medium surrounding these stars. We discuss this next.

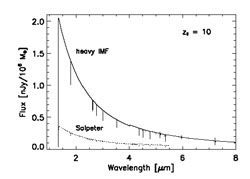Figure 37. Comparison of the predicted flux from a Pop III star cluster at zs = 10 for a Salpeter IMF (Tumlinson & Shull 2000 [370]) and a massive IMF (Bromm et al. 2001 [59]). Plotted is the observed flux (in nJy per 106 M of stars) vs. observed wavelength (in µm) for a flat Universe with = 0.7 and h = 0.65. Solid line: The case of a heavy IMF. Dotted line: The fiducial case of a standard Salpeter IMF. The cutoff below obs = 1216 Å (1 + zs) = 1.34 µm is due to complete Gunn-Peterson absorption (which is artificially assumed to be sharp). Clearly, for the same total stellar mass, the observable flux is larger by an order of magnitude for stars which are biased towards having masses > 100 M.

5.5. Emission of Recombination Lines from the First Galaxies

The hard UV emission from a star cluster or a quasar at high redshift is likely reprocessed by the surrounding interstellar medium, producing very strong recombination lines of hydrogen and helium (Oh 1999 [270]; Tumlinson & Shull 2000 [370]; see also Baltz, Gnedin & Silk 1998 [17]). We define 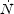_ion to be the production rate of ionizing photons by the source. The emitted luminosity L_line^em per unit stellar mass in a particular recombination line is then estimated to be

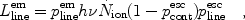(111)

where p_line^em is the probability that a recombination leads to the emission of a photon in the corresponding line, is the frequency of the line and p_cont^esc and p_line^esc are the escape probabilities for the ionizing photons and the line photons, respectively. It is natural to assume that the stellar cluster is surrounded by a finite H II region, and hence that p_cont^esc is close to zero [387, 302]. In addition, p_line^esc is likely close to unity in the H II region, due to the lack of dust in the ambient metal-free gas. Although the emitted line photons may be scattered by neutral gas, they diffuse out to the observer and in the end survive if the gas is dust free. Thus, for simplicity, we adopt a value of unity for p_line^esc.

As a particular example we consider case B recombination which yields p_line^em of about 0.65 and 0.47 for the Ly and He II 1640 Å lines, respectively. These numbers correspond to an electron temperature of ~ 3 × 10⁴K and an electron density of ~ 10² - 10³ cm^-3 inside the H II region [354]. For example, we consider the extreme and most favorable case of metal-free stars all of which are more massive than ~ 100 M. In this case L_line^em = 1.7 × 10³⁷ and 2.2 × 10³⁶ erg s^-1 M^-1 for the recombination luminosities of Ly and He II 1640 Åper stellar mass [59]. A cluster of 10⁶ M in such stars would then produce 4.4 and 0.6 × 10⁹ L in the Ly and He II 1640 Å lines. Comparably-high luminosities would be produced in other recombination lines at longer wavelengths, such as He II 4686 Å and H [270, 271].

The rest - frame equivalent width of the above emission lines measured against the stellar continuum of the embedded star cluster at the line wavelengths is given by

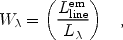(112)

where L is the spectral luminosity per unit wavelength of the stars at the line resonance. The extreme case of metal-free stars which are more massive than 100 M yields a spectral luminosity per unit frequency L = 2.7 × 10²¹ and 1.8 × 10²¹ erg s^-1 Hz^-1 M^-1 at the corresponding wavelengths [59]. Converting to L, this yields rest-frame equivalent widths of W = 3100 Å and 1100 Å for Ly and He II 1640 Å, respectively. These extreme emission equivalent widths are more than an order of magnitude larger than the expectation for a normal cluster of hot metal-free stars with the same total mass and a Salpeter IMF under the same assumptions concerning the escape probabilities and recombination [209]. The equivalent widths are, of course, larger by a factor of (1 + z_s) in the observer frame. Extremely strong recombination lines, such as Ly and He II 1640 Å, are therefore expected to be an additional spectral signature that is unique to very massive stars in the early Universe. The strong recombination lines from the first luminous objects are potentially detectable with JWST [271].

⁶ See http://www.ukaff.ac.uk/starcluster for an animation. Back.

⁷ Note, however, that feedback from a single GRB or supernova on the gas confined within early dwarf galaxies could be dramatic, since the binding energy of most galaxies at z > 10 is lower than 10⁵¹ ergs [23]. Back.