5. SCATTERING OF LIGHT BY DUST: ANALYTIC SOLUTIONS

For dust with sizes much smaller than the wavelength of the incident radiation, analytic solutions to the light scattering problem exist for certain shapes. Let a be the characteristic length of the dust, and x 2 a / be the dimensionless size parameter. Under the condition of x << 1 and |mx| << 1 (i.e. in the "Rayleigh" regime), C_abs = 4 k Im{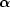}, C_sca = (8/3) k⁴ |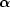|², where 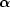is the complex electric polarizability of the dust. Apparently, C_sca << C_abs and C_ext C_abs. In general, 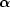is a diagonalized tensor; ⁷ for homogeneous spheres composed of an isotropic material, it is independent of direction

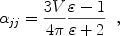(32)

where V is the dust volume. ⁸ For a homogeneous, isotropic ellipsoid, the polarizability for electric field vector parallel to its principal axis j is

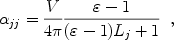(35)

where L_j is the "depolarization factor" along principal axis j (see [13]). The electric polarizability 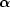is also known for concentric core-mantle spheres [69], confocal core-mantle ellipsoids [13, 19], and multi-layered ellipsoids of equal-eccentricity [18]. For a thin conducting cylindrical rod with length 2l and radius r_a << l, the polarizability along the axis of the rod is [38]

(36)

In astronomical modeling, the most commonly invoked grain shapes are spheres and spheroids (oblates or prolates). ⁹ In the Rayleigh regime, their absorption and scattering properties are readily obtained from Eqs. (32,35). For both dielectric and conducting spheres (as long as x << 1 and |mx| << 1)

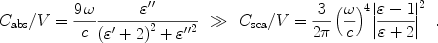(37)

At long wavelengths, for dielectric dust " while ' approaches a constant much larger than " (see Eqs. 18,19), we see C_abs " ²; for metallic dust, " 1/ while ' approaches a constant much smaller than " (see Eqs. 22,23), we see C_abs / " ²; therefore, for both dielectric and metallic dust C_abs ^-2 at long wavelengths! ¹⁰

It is also seen from Eq. (37) that for spherical dust in the Rayleigh regime the albedo 0, and the radiation cross section C_pr C_abs. This has an interesting implication. Let _pr(a) be the ratio of the radiation pressure force to the gravity of a spherical grain of radius a in the solar system or in debris disks illuminated by stars (of radius R_* and mass M_*) with a stellar flux of F^* at the top of the atmosphere [53],

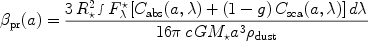(38)

where G is the gravitational constant, and _dust is the mass density of the dust. For grains in the Rayleigh regime (g 0; C_sca << C_abs; C_abs a³), we see _pr C_abs / a³ is independent of the grain size a (see Fig. 4)!

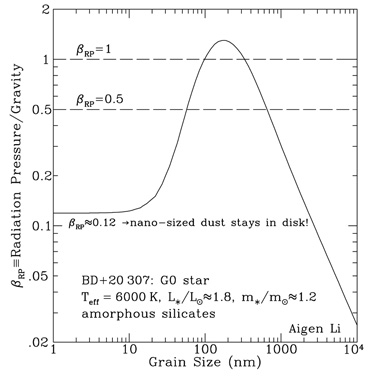Figure 4. pr - Ratio of radiation pressure to gravity for compact silicate grains in the debris disk around the Sun-like star BD+20 307 (G0, age ~ 300 Myr). We note for nano-sized grains pr 0.12, independent of grain size; for grains larger than ~ 0.3 µm, pr is inverse proportional to grain size. Song et al. [68] attributed the dust in this disk to recent extreme collisions between asteroids. Taken from [51].

Spheroids are often invoked to model the interstellar polarization. In the Rayleigh approximation, their absorption cross sections for light polarized parallel (||) or perpendicular () to the grain symmetry axis are ¹¹

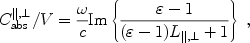(39)

where the depolarization factors parallel (L_||) or perpendicular (L) to the grain symmetry axis are not independent, but related to each other through L_|| + 2L = 1, with

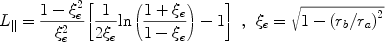(40)

for prolates (r_a > r_b) where _e is the eccentricity, and

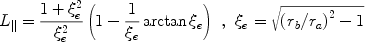(41)

for oblates (r_a < r_b). For spheres L_|| = L = 1/3 and _e = 0. For extremely elongated prolates or "needles" (r_a >> r_b), it is apparent C_abs << C_abs^||, we thus obtain

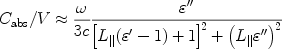(42)

where L_|| (r_b / r_a)² ln(r_a / r_b). For dielectric needles, C_abs " ^-2 at long wavelengths since L_||(' - 1) + 1 >> L_||" (see [45]); for metallic needles, for a given value of " one can always find a sufficiently long needle with L_|| " < 1 and L_||(' - 1) << 1 so that C_abs " which can be very large (see [45]). Because of their unique optical properties, metallic needles with high electrical conductivities (e.g. iron needles, graphite whiskers) are resorted to explain a wide variety of astrophysical phenomena: (1) as a source of starlight opacity to create a non-cosmological microwave background by the thermalization of starlight in a steady-state cosmology [27]; (2) as a source of the grey opacity needed to explain the observed redshift-magnitude relation of Type Ia supernovae without invoking a positive cosmological constant [1]; (3) as the source for the submm excess observed in the Cas A supernova remnant [16]; and (4) as an explanation for the flat 3-8 µm extinction observed for lines of sight toward the Galactic Center and in the Galactic plane [15]. However, caution should be taken in using Eq. 42 (i.e. the Rayleigh approximation) since the Rayleigh criterion 2 r_a |m| / << 1 is often not satisfied for highly conducting needles (see [45]). ¹²

In astronomical spectroscopy modeling, the continuous distribution of ellipsoid (CDE) shapes has been widely used to approximate the spectra of irregular dust grains by averaging over all ellipsoidal shape parameters [6]. In the Rayleigh limit, this approach, assuming that all ellipsoidal shapes are equally probable, has a simple expression for the average cross section

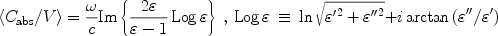(43)

where Log is the principal value of the logarithm of . The CDE approach, resulting in a significantly-broadened spectral band (but with its maximum reduced), seems to fit the experimental absorption spectra of solids better than Mie theory. Although the CDE may indeed represent a distribution of shape factors caused either by highly irregular dust shapes or by clustering of spherical grains into irregular agglomerates, one should caution that the shape distribution of cosmic dust does not seem likely to resemble the CDE, which assumes that extreme shapes like needles and disks are equally probable. A more reasonable shape distribution function would be like dP / dL_|| = 12 L_|| (1 - L_||)² which peaks at spheres (L^|| = 1/3). This function is symmetric about spheres with respect to eccentricity e and drops to zero for the extreme cases: infinitely thin needles (e 1, L_|| 0) or infinitely flattened pancakes (e , L_|| 1). Averaging over the shape distribution, the resultant absorption cross section is C_abs = ₀¹ dL_|| dP / dL_|| C_abs(L_||) where C_abs(L_||) is the absorption cross section of a particular shape L_|| [62, 49, 48]. Alternatively, Fabian et al. [17] proposed a quadratic weighting for the shape distribution, "with near-spherical shapes being most probable".

When a dust grain is very large compared with the wavelength, the electromagnetic radiation may be treated by geometric optics: Q_ext C_ext / C_geo 2 if x 2 a / >> 1 and |m - 1| x >> 1. ¹³ For these grains (g 1; C_abs C_geo), the ratio of the radiation pressure to gravity _pr C_abs / a³ 1 / a. This is demonstrated in Figure 4. For dust with x >> 1 and |m - 1| x << 1, one can use the "anomalous diffraction" theory [69]. For dust with |m - 1| x << 1 and |m - 1| << 1, one can use the Rayleigh-Gans approximation ¹⁴ to obtain the absorption and scattering cross sections [6 39 69]:

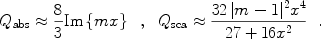(44)

It is important to note that the Rayleigh-Gans approximation is invalid for modeling the X-ray scattering by interstellar dust at energies below 1 keV. This approximation systematically and substantially overestimates the intensity of the X-ray halo below 1 keV [66].

⁷ 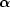can be diagonalized by appropriate choice of Cartesian coordinate system. It describes the linear response of a dust grain to applied electric field E: p = 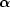E where p is the induced electric dipole moment. Back.

⁸ For a dielectric sphere with dielectric function given in Eq. (17), in the Rayleigh regime the absorption cross section is

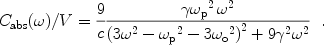(33)

Similarly, for a metallic sphere with dielectric function given in Eq. (21),

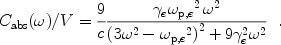(34)

It is seen that the frequency-dependent absorption cross section for both dielectric and metallic spheres is a Drude function. This is also true for ellipsoids. Back.

⁹ Spheroids are a special class of ellipsoids. Let r_a, r_b, and r_c be the semi-axes of an ellipsoid. For spheroids, r_b = r_c. Prolates with r_a > r_b are generated by rotating an ellipse (of semi-major axis r_a and semi-minor axis r_b) about its major axis; oblates with r_a < r_b are generated by rotating an ellipse (of semi-minor axis r_a and semi-major axis r_b) about its minor axis. Back.

¹⁰ However, various astronomical data suggest a flatter wavelength-dependence (i.e. C_abs ^- with < 2): < 2 in the far-IR/submm wavelength range has been reported for interstellar molecular clouds, circumstellar disks around young stars, and circumstellar envelopes around evolved stars. Laboratory measurements have also found < 2 for certain cosmic dust analogues. In literature, the flatter ( < 2) long-wavelength opacity law is commonly attributed to grain growth by coagulation of small dust into large fluffy aggregates (see [47] and references therein). However, as shown in Eq. (31), the Kramers-Kronig relation requires that should be larger than 1 for since F is a finite number and the integration in the left-hand-side of Eq. (31) should be convergent although we cannot rule out < 1 over a finite range of wavelengths. Back.

¹¹ For grains spinning around the principal axis of the largest moment of inertia, the polarization cross sections are C_pol = (C_abs^|| - C_abs) / 2 for prolates, and C_pol = (C_abs - C_abs^||) for oblates; the absorption cross sections for randomly-oriented spheroids are C_abs = (C_abs^|| + 2C_abs) / 3 [42]. Back.

¹² The "antenna theory" has been applied for conducting needle-like dust to estimate its absorption cross sections [75]. Let it be represented by a circular cylinder of radius r_a and length l (r_a << l). Let _R be its resistivity. The absorption cross section is given by C_abs = (4 / 3c)( r_a² l / _R), with a long wavelength cutoff of _o = _R c (l / r_a)² / ln(l / r_a)², and a short-wavelength cutoff of _min (2 c m_e) / (_R n_e e²), where m_e, e, and n_e are respectively the mass, charge, and number density of the charge-carrying electrons. Back.

¹³ At a first glance, Q_ext 2 appears to contradict "common sense" by implying that a large grain removes twice the energy that is incident on it! This actually can be readily understood in terms of basic optics principles: (1) on one hand, all rays impinging on the dust are either scattered or absorbed. This gives rise to a contribution of C_geo to the extinction cross section. (2) On the other hand, all the rays in the field which do not hit the dust give rise to a diffraction pattern that is, by Babinet's principle, identical to the diffraction through a hole of area C_geo. If the detection excludes this diffracted light then an additional contribution of C_geo is made to the total extinction cross section [6]. Back.

¹⁴ The conditions for the Rayleigh-Gans approximation to be valid are |m - 1| << 1 and |m - 1| x << 1. The former ensures that the reflection from the surface of the dust is negligible (i.e. the impinging light enters the dust instead of being reflected); the latter ensures that the phase of the incident wave is not shifted inside the dust. For sufficiently small scattering angles, it is therefore possible for the waves scattered throughout the dust to add coherently. The intensity (I) of the scattered waves is proportional to the number (N) of scattering sites squared: I N^{2 2} a⁶ (where is the mass density of the dust). This is why the X-ray halos (usually within ~ 1° surrounding a distant X-ray point source; [63]) created by the small-angle scattering of X-rays by interstellar dust are often used to probe the size (particularly the large size end; [14, 67, 73]), morphology (compact or porous; [58, 66]), composition, and spatial distribution of dust. Back.