3. OBSERVATIONALLY INFERRED PRIMORDIAL ABUNDANCES

3.1. The Primordial Deuterium Abundance

Deuterium is the baryometer of choice since its post-BBN evolution is simple (and monotonic!) and its BBN-predicted relic abundance depends sensitively on the baryon abundance (y_{D B}^-1.6). As the most weakly bound of the light nuclides, any deuterium cycled through stars is burned to ³He and beyond during the pre-main sequence, convective (fully mixed) evolutionary stage [15]. Thus, deuterium observed anywhere, anytime, should provide a lower bound to the primordial D abundance. For "young" systems at high redshift and/or with very low metallicity, which have experienced very limited stellar evolution, the observed D abundance should be close to the primordial value. Thus, although there are observations of deuterium in the solar system and the interstellar medium (ISM) of the Galaxy which provide interesting lower bounds to the primordial abundance, it is the observations of relic D in a few (too few!), high redshift, low metallicity, QSO absorption line systems (QSOALS) which are of most value in enabling estimates of its primordial abundance.

In contrast to the great asset of the simple post-BBN evolution, the identical absorption spectra of D I and H I (modulo the velocity/wavelength shift resulting from the heavier reduced mass of the deuterium atom) is a severe liability, limiting drastically the number of useful targets in the vast Lyman-alpha forest of QSO absorption spectra (see Kirkman et al. [16] for further discussion). As a result, it is essential to choose target QSOALS whose velocity structure is "simple" since a low column density H I absorber, shifted by ~ 81 km/s with respect to the main H I absorber (an "interloper") could masquerade as D I absorption [17]. If this degeneracy is not recognized, a D/H ratio which is too high could be inferred. Since there are many more low-column density absorbers than those with high H I column densities, absorption systems with somewhat lower H I column density (e.g., Lyman-limit systems: LLS) may be more susceptible to this contamination than the higher H I column density absorbers (e.g., damped Ly absorbers: DLA). While the DLA do have many advantages over the LLS, a precise determination of the H I column density utilizing the damping wings of the H I absorption requires an accurate placement of the continuum, which could be compromised by H I interlopers. This might lead to errors in the H I column density. These complications are real and the path to primordial D using QSOALS has not been straightforward, with some abundance claims having had to be withdrawn or revised. Through 2003 there were only five "simple" QSOALS with deuterium detections leading to reasonably robust abundance determinations [16] (and references therein); these are shown in Figure 4 along with the corresponding solar system and ISM D abundances. It is clear from Figure 4, that there is significant dispersion among the derived D abundances at low metallicity which, so far, masks the anticipated primordial deuterium plateau, suggesting that systematic (or random) errors, whose magnitudes are hard to estimate, may have contaminated the determinations of the D I and/or H I column densities.

Figure 4. The observationally inferred primordial deuterium abundances (the ratio of D to H by number) versus a logarithmic measure of the metallicity, relative to solar ([Si/H]), for five high redshift, low metallicity QSOALS (filled circles) through 2003. The error bars are the quoted 1 uncertainties. Also shown for comparison are the D/H ratios inferred from observations of the local interstellar medium (ISM; filled square) and that for the pre-solar nebula (Sun; filled triangle).

It might be hoped that as more data are acquired, the excessive dispersion among the deuterium abundances seen in Fig. 4 would decrease leading to a better defined deuterium plateau. Be careful what you wish for! In 2004, Crighton et al. [18] identified deuterium absorption in another high redshift, low metallicity QSOALS and derived its abundance. The updated version of Fig. 4 is shown in Fig. 5. Now, the dispersion is larger! The low value of the Crighton et al. [18] D abundance, similar to that in the more highly evolved ISM and the pre-solar nebula, is puzzling. D. Tytler (private communication) and colleagues have data (unpublished) for the same QSOALS and they find acceptable fits with lower H I column densities and no visible D I; perhaps this system is contaminated by an interloper [17]. The two low D/H ratios, if not affected by random or systematic errors, may be artifacts of a small statistical sample or, they may have resulted from "young" regions in which some of the relic deuterium has been destroyed or depleted onto dust [19]. These suggestions pose challenges since any cycling of gas through stars should have led to an increase in the heavy element abundances (these QSOALS are metal poor) and, at low metallicity the amount of dust is expected to be small.

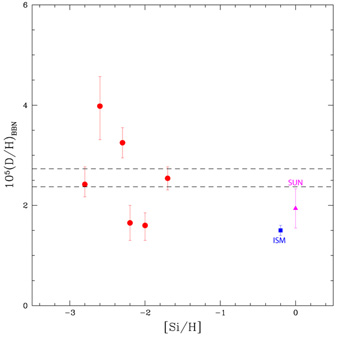Figure 5. Figure 4 updated to 2004 to include the one new deuterium abundance determination18 for a high redshift, low metallicity QSOALS. The dashed lines show the SBBN-predicted 1 band for the WMAP baryon abundance.

For the Spergel et al. [2] baryon abundance of ₁₀ = 6.14 ± 0.25, the SBBN-predicted deuterium abundance is y_D = 2.6 ± 0.2. As may be seen in Fig. 5, the current data exhibit the Goldilocks effect: two D/H ratios are "too small", two are "too large", and two are "just right". Nonetheless, it is clear that the sparse data currently available are in very good agreement with the SBBN prediction. If the weighted mean of D/H for the six QSOALS is adopted, but the dispersion in the mean is used in place of the error in the mean, y_D = 2.4 ± 0.4, corresponding to an SBBN-predicted baryon abundance of ₁₀ = 6.4 ± 0.6, in excellent agreement with the WMAP value. Were it not for the excessive dispersion among the extant deuterium abundance determinations, the precision of the baryon abundance determined from SBBN would be considerably enhanced. For example, if the formal error in the mean is used, ₁₀ = 6.4 ± 0.2 is the deuterium-based, SBBN prediction, very close to that for the baryon abundance derived from the CBR alone [2] (₁₀^WMAP = 6.3 ± 0.3). More data is crucial to deuterium fulfilling its potential.

3.2. The Primordial Helium-3 Abundance

The post-BBN evolution of ³He, involving competition among stellar production, destruction, and survival, is considerably more complex and model dependent than that of D. Interstellar ³He incorporated into stars is burned to ⁴He (and beyond) in the hotter interiors, but it is preserved in the cooler, outer layers. Furthermore, while hydrogen burning in cooler, low-mass stars is a net producer of ³He [20], it is unclear how much of this newly synthesized ³He is returned to the interstellar medium and how much of it is consumed in post-main sequence evolution (e.g., Sackmann & Boothroyd [21]). For years it had been anticipated that net stellar production would prevail in this competition, so that the ³He abundance would increase with time (and with metallicity) [22].

Observations of ³He, are restricted to the solar system and the Galaxy. Since for the latter there is a clear gradient of metallicity with location, a gradient in ³He abundance was also expected. However, as is clear from Figures 6 & 7, the data [23, 24] reveal no statistically significant correlation between the ³He abundance and metallicity or location in the Galaxy, suggesting a very delicate balance between net production and net destruction of ³He. For a recent review of the current status of ³He evolution, see Romano et al. [25].

Figure 6. The 3He abundance determinations (by number relative to H) in the ISM of the Galaxy (from BRB24) as a function of the corresponding oxygen abundances. The solar symbol indicates the 3He abundance for the pre-solar nebula. The dashed lines show the 1 band adopted by BRB.

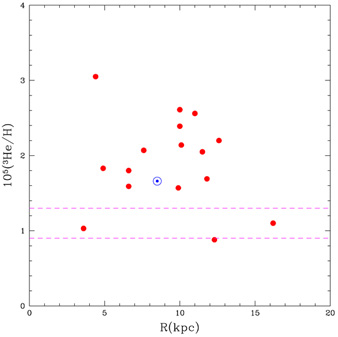Figure 7. As in Figure 6 but, for the 3He abundances as a function of distance from the center of the Galaxy.

While the absence of a gradient suggests the mean ("plateau") ³He abundance in the Galaxy (y₃ 1.9 ± 0.6) might provide a good estimate of the primordial abundance, Bania, Rood & Balser (BRB) [24] prefer to adopt as an upper limit to the primordial abundance, the ³He abundance measured in the most distant (from the Galactic center), most metal poor, Galactic H II region, y₃ 1.1 ± 0.2; see Figs. 6 & 7. This choice is in excellent agreement with the SBBN/WMAP predicted abundance of y₃ = 1.04 ± 0.04 (see Section 2.2). While both D and ³He are consistent with the SBBN predictions, ³He is a less sensitive baryometer than is D since (D/H)_{BBN B}^-1.6, while (³He/H)_{BBN B}^-0.6. For example, if y₃ = 1.1 ± 0.2 is adopted for the ³He primordial abundance, ₁₀(³He) = 6.0 ± 1.7. While the central value of the ³He-inferred baryon density parameter is in nearly perfect agreement with the WMAP value [2], the allowed range of _B is far too large to be very useful. Still, ³He can provide a valuable BBN consistency check.

3.3. The Primordial Helium-4 Abundance

The post-BBN evolution of ⁴He is quite simple. As gas cycles through generations of stars, hydrogen is burned to helium-4 (and beyond), increasing the ⁴He abundance above its primordial value. The ⁴He mass fraction in the Universe at the present epoch, Y₀, has received a significant contribution from post-BBN, stellar nucleosynthesis, so that Y₀ > Y_P. However, since the "metals" such as oxygen are produced by short-lived, massive stars and ⁴He is synthesized (to a greater or lesser extent) by all stars, at very low metallicity the increase in Y should lag that in e.g., O/H so that as O/H 0, Y Y_P. As is the case for deuterium and lithium, a ⁴He "plateau" is expected at sufficiently low metallicity. Therefore, although ⁴He is observed in the Sun and in Galactic H II regions, the key data for inferring its primordial abundance are provided by observations of helium and hydrogen emission (recombination) lines from low-metallicity, extragalactic H II regions. The present inventory of such regions studied for their helium content exceeds 80 (see Izotov & Thuan (IT) [26]). Since with such a large data set even modest observational errors for the individual H II regions can lead to an inferred primordial abundance whose formal statistical uncertainty may be quite small, special care must be taken to include hitherto ignored or unaccounted for systematic corrections and/or errors. It is the general consensus that the present uncertainty in Y_P is dominated by the latter, rather than by the former errors. Indeed, many of the potential pitfalls were identified by Davidson & Kinman [27] in a prescient, 1985 paper. In the abstract they say, "The most often quoted estimates of the primordial helium abundance are optimistic in the sense that quoted uncertainties usually do not include some potentially serious systematic errors."

To provide a context for the discussion of the most recent data and analyses, Figure 8 offers a compilation of the history of Y_P determinations [26, 28] derived using data from low metallicity, extragalactic H II regions. Notice that all of these estimates, taken at face value, fall below the SBBN/WMAP predicted primordial abundance by at least 2, reemphasizing the importance of accounting for systematic uncertainties. With this in mind, we turn to recent reanalyses [29, 30] of the IT data [26], supplemented by key observations of a local, higher metallicity H II region [30].

Figure 8. The observationally inferred primordial 4He mass fractions from 1978 until 2004. The error bars are the quoted 1 uncertainties. Also shown is the SBBN-predicted relic abundance (solid line) for the WMAP baryon abundance, along with the 1 uncertainty (dashed lines) of the SBBN prediction.

Prior and subsequent to the Davidson & Kinman paper [27] astronomers have generally been aware of the important sources of potential systematic errors associated with using recombination line data to infer the helium abundance. However, attempts to account for them have often been unsystematic or, entirely absent. The current conventional wisdom that the accuracy of the data demands their inclusion has led to some attempts to account for a few of them or, for combinations of a few of them [26, 29, 30, 31, 32]. The Olive & Skillman (OS) [29] analysis of the IT data is the most systematic to date. Following criteria outlined in their 2001 paper [29], OS found they were able to apply their analysis to only 7 of the 82 IT H II regions. This tiny data set, combined with its limited range in metallicity (oxygen abundance), severely limits the statistical significance of any conclusions OS can extract from it. In Figure 9 are shown the differences between the OS-inferred and the IT-inferred helium abundances. For these seven H II regions there is no evidence that Y Y^OS - Y^IT is correlated with metallicity. The weighted mean offset along with the error in the mean are Y = 0.0029 ± 0.0032 (the average offset and the average error are Y = 0.0009 ± 0.0095), consistent with zero at 1.

Figure 9. The differences between the OS and IT 4He abundances, Y YOS - YIT for the OS-selected IT H II regions versus the corresponding oxygen abundances. The solid line is the weighted mean of the helium mass fraction differences, while the dashed line shows the unweighted average of the differences.

If the weighted mean offset is applied to the IT-derived primordial abundance of Y_P^IT = 0.2443 ± 0.0015, the "corrected" primordial value becomes

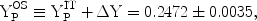(25)

leading to a 2 upper bound on the primordial abundance of Y_P^OS 0.254. In contrast, OS prefer to fit these seven data points to a linear Y versus O/H relation and, from it, derive the primordial abundance. Their IT-revised abundances, along with, for comparison, that from their reanalysis of the Peimbert et al. [30] data for an H II region in the SMC (to be discussed next), are shown in Figure 10. It is not surprising that for only seven data points, each with larger errors than those adopted by IT, spanning such a narrow range in metallicity, their linear fit, Y₇^OS = 0.2495 ± 0.0092 + (54 ± 187)(O/H), is not statistically significant. Indeed, it is not preferred over the simple weighted mean of the seven helium abundances (0.252 ± 0.003), since the ² per degree of freedom is actually higher for the linear fit. In fact, there is no statistically significant correlation between Y and O/H for the IT-derived abundances for these seven H II regions either. As valuable as is their reanalysis of the IT data, the OS conclusion that Y_P = 0.249 ± 0.009 is not supported by the sparse data set they used ⁴. Unless and until an analysis is performed of a much larger data set, with a longer metallicity baseline, the estimate in eq. 25, and its corresponding 2 upper bound, may provide a good starting point at present for an approach to the primordial abundance of ⁴He.

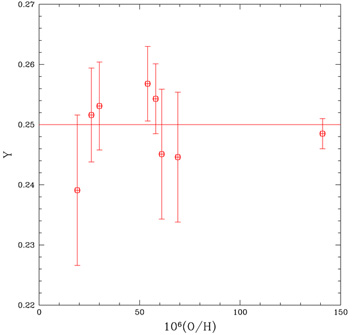Figure 10. The OS-revised 4He versus oxygen abundances for the seven IT H II regions and the SMC H II region from PPR. The solid line is the weighted mean of the helium abundances for all eight of the H II regions reanalyzed by OS.

Another correction, not directly constrained by the analysis of OS, is related to the inhomogeneous nature of H II regions. Unlike classical, textbook, homogeneous, Strömgren spheres, real H II regions are filamentary and inhomogeneous, with variations in electron density and temperature likely produced by shocks and winds from pockets of hot, young stars. Esteban and Peimbert [33] have noted that temperature fluctuations can have a direct effect on the helium abundance derived from recombination lines. This effect was investigated theoretically using models of H II regions [31], but more directly by Peimbert et al. [30] using data from a nearby, spatially resolved, H II region in the Small Magellanic Cloud (SMC), along with their reanalyses of four H II regions selected from IT. While the SMC H II region formed out of chemically evolved gas and, therefore, cannot be used by itself to derive primordial abundances, the spatial resolution it offers permits a direct investigation of many potential systematic effects. In particular, since recombination lines are used, the observations are blind to any neutral helium or hydrogen. Estimates of the "ionization correction factor" (icf), while model dependent, are large [32]. For example, using models of H II regions ionized by distributions of stars of different masses and ages and comparing to the IT (1998) data, Gruenwald et al. [32] concluded that IT overestimated the primordial ⁴He abundance by Y^GSV(icf) 0.006 ± 0.002; Sauer & Jedamzik [32] find a similar, even larger, correction. If this correction is applied to the OS-revised, IT primordial abundance in eq. 25, the new, icf-corrected value is

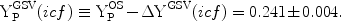(26)

In addition to the subset of 7 of the 82 IT H II regions which meet their criteria, OS also reanalyzed the Peimbert et al. data [30] for the SMC H II region. This OS-revised data point is shown in Figure 10 at the highest oxygen abundance. Notice that the eight data points plotted in Fig. 10 show no evidence of the expected increase of Y with metallicity ⁵; this is likely due to the small sample size. The weighted mean ⁴He abundance for these eight H II regions is Y₈^OS = 0.250 ± 0.002, corresponding to a 2 upper bound of Y_P 0.254. Coincidentally, this is the same 2 upper bound as that found from the mean of the seven IT H II regions (see eq. 25) and, also, the 2 upper bound from the OS-reanalyzed SMC H II region alone. If the ionization corrections from Gruenwald et al. [32] are applied to each of these eight H II regions, it is found that the mean Y(icf)₈ = -0.002 ± 0.002, so that including this correction, while accounting for the increased error, leaves the 2 upper bound of Y_P 0.254 unchanged.

The lesson from the discussion above is that while recent attempts to determine the primordial abundance of ⁴He may have achieved high precision, their accuracy remains in question. The latter is limited by our understanding of and our ability to account for systematic errors and biases, not by the statistical uncertainties. The good news is that carefully organized, detailed studies of only a few (~ a dozen?) low metallicity, extragalactic H II regions may go a long way towards an accurate determination of Y_P. The bad news is that many astronomers and telescope allocation committee members are unaware that this is an interesting and important problem, worth their effort and telescope time. At present then, the best that can be done is to adopt a defensible value for Y_P and, especially, its uncertainty. To this end, in the following the estimate in eq. 26 is chosen: Y_P = 0.241 ± 0.004. While the central value of Y_P is low, it is within 2 (~ 1.75) of the SBBN/WMAP expected central value of Y_P = 0.248 (see Section 2.2). Note that the extrapolation of the linear fit of the {Y, O/H} data from the lowest metallicity (O/H 2 × 10^-5) to zero metallicity (Y_P) corresponds to Y 0.0009, well within the uncertainties of Y_P.

In setting contraints on new physics, an upper bound to Y_P is required. A robust upper bound suggested by the above discussion is Y_P 0.254. As an example, the SBBN/WMAP lower bound (at ~ 2) to Y_P is 0.247, so that Y_P < 0.007. This corresponds to the robust upper bounds S < 1.04 and N < 3.5, eliminating (just barely) even one, new, light scalar, and bounding the lepton asymmetry from below: _e > -0.03.

3.4. The Primordial Lithium-7 Abundance

In the post-BBN universe ⁷Li, along with ⁶Li, ⁹Be, ¹⁰B, and ¹¹B, is produced in the Galaxy by cosmic ray spallation/fusion reactions. Furthermore, observations of super-lithium rich red giants provide evidence that (at least some) stars are net producers of lithium. Therefore, even though lithium is easily destroyed in the hot interiors of stars, theoretical expectations supported by the observational data shown in Figure 11 suggest that while lithium may have been depleted in many stars, the overall trend is that its abundance has increased with time. Therefore, in order to probe the BBN yield of ⁷Li, it is necessary to restrict attention to the oldest, most metal-poor halo stars in the Galaxy (the "Spite Plateau") seen at low metallicity in Fig. 11. Using a selected set of the lowest metallicity halo stars, Ryan et al. [34] claim evidence for a 0.3 dex increase in the lithium abundance ([Li] 12 + log(Li/H)) for -3.5 [Fe/H] -1, and they derive a primordial abundance of [Li]_P 2.0-2.1. This abundance is low compared to the value found by Thorburn [35], who derived [Li]_P 2.25 ± 0.10. The stellar temperature scale plays a key role in using the observed equivalent widths to derive the ⁷Li abundance. Studies of halo and Galactic Globular Cluster stars employing the infrared flux method effective temperature scale suggest a higher lithium plateau abundance [36]: [Li]_P = 2.24 ± 0.01, similar to Thorburn's [35] value. Recently, Melendez & Ramirez [37] reanalyzed 62 halo dwarfs using an improved infrared flux method effective temperature scale. While they failed to confirm the [Li] - [Fe/H] correlation claimed by Ryan et al. [34], they suggest an even higher relic lithium abundance: [Li]_P = 2.37 ± 0.05. A very detailed and careful reanalysis of extant observations with great attention to systematic uncertainties and the error budget has been done by Charbonnel and Primas [38], who find no convincing evidence for a Li trend with metallicity, deriving [Li]_P = 2.21 ± 0.09 for their full sample and [Li]_P = 2.18 ± 0.07 when they restrict their sample to unevolved (dwarf) stars. They suggest the Melendez & Ramirez value should be corrected downwards by 0.08 dex to account for different stellar atmosphere models, bringing it into closer agreement with their results. To err on the side of conservatism, the lithium abundance of Melendez & Ramirez [37], [Li]_P = 2.37 ± 0.05, which is closer to the SBBN expectation, will be adopted in further comparisons.

Figure 11. Lithium abundances, log є(Li) [Li] 12 + log(Li/H) versus metallicity (on a log scale relative to solar) from a compilation of stellar observations by V. V. Smith. The solid line is intended to guide the eye to the "Spite Plateau".

There is tension between the SBBN predicted relic abundance of ⁷Li ([Li]_P = 2.65_-0.06^+0.05; see Section 2.2) and that derived from recent observational data ([Li]_P = 2.37 ± 0.05). Systematic errors may play a large role confirming or resolving this factor of two discrepancy. The role of the stellar temperature scale has already been mentioned. Another concern is associated with the temperature structures of the atmospheres of these very cool, metal-poor stars. This can be important because a large ionization correction is needed since the observed neutral lithium is a minor component of the total lithium. Furthermore, since the low metallicity, dwarf, halo stars used to constrain primordial lithium are among the oldest in the Galaxy, they have had the most time to alter (by dilution and/or destruction) their surface lithium abundances, as is seen to be important for many of the higher metallicity stars shown in Fig. 11. While mixing stellar surface material to the interior would destroy or dilute any prestellar lithium, the very small observed dispersion among the lithium abundances in the low metallicity halo stars (in contrast to the very large spread for the higher metallicity stars) suggests this correction may not be large enough ( 0.1-0.2 dex at most) to bridge the gap between theory and observation; see, e.g., Pinsonneault et al. [39] and further references therein.

⁴ Note that OS used the corresponding 1 upper bound of 0.258 for the upper bound to their "favored" primordial abundance range. Back.

⁵ Absence of evidence is NOT evidence of absence. Back.