2. WHIM HEATING AND ION TEMPERATURE EVOLUTION

The plasma ion heating in the WHIM is most likely due to cosmological shocks. The Alfvén Mach number of a shock propagating through an ionised gas of local overdensity = / < > at the epoch z in the standard CDM cosmology is determined by

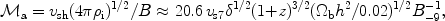(1)

where B_-9 is the magnetic field just before the shock, measured in nG and v_s7 is the shock velocity in 10⁷cm s^-1, and < > is the average density in the Universe.

The sonic Mach number for a shock propagating in a plasma of standard cosmic abundance is

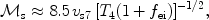(2)

where T₄ is the plasma ion temperature measured in 10⁴ K (typical for a preshock photoionised plasma) and f_ei = T_e / T_i. An important plasma parameter is

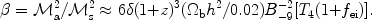It is the ratio of the thermal and magnetic pressures. In hot X-ray clusters of galaxies the beta parameter is ~ 100 for ~ µG magnetic fields in the clusters. The most uncertain parameter is the magnetic field value in the WHIM allowing for both ~ 1 and >> 1 cases.

In a supercritical collisionless shock the conversion of kinetic energy of an initially cold flow to the ion distribution with high kinetic temperature occurs in the thin ion viscous jump. The width of the ion viscous jump _vi in a collisionless shock propagating through a plasma with ~ 1 is typically of the order of a ten to a hundred times of the ion inertial length l_i defined as l_i = c/_pi 2.3 × 10⁷ n^-0.5 cm. Here _pi is the ion plasma frequency. The ion inertial length in the WHIM can be estimated as

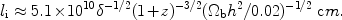The width of the shock transition region for magnetic field is also 10 l_i for a quasi-perpendicular shock, but it is often about ten times wider for quasi-parallel shocks.

Properties of nonrelativistic shocks in a hot, low magnetised plasma with high >> 1 are yet poorly studied. Measurements from the ISEE 1 and ISEE 2 spacecrafts were used by Farris et al. (1992) to examine the terrestrial bow shock under high beta conditions. These measurements were compared with and found to be in agreement with the predicted values of the Rankine-Hugoniot relations using the simple adiabatic approximation and a ratio of specific heats, , of 5/3. Large magnetic field and density fluctuations were observed, but average downstream plasma conditions well away from the shock were relatively steady, near the predicted Rankine-Hugoniot values. The magnetic disturbances persisted well downstream and a hot, dense ion beam was detected leaking from the downstream region of the shock. The observation proved the existence of collisionless shocks in high beta plasma, but a detailed study of high beta shock structure is needed for cosmological plasmas.

We discuss in the next section the ion heating in collisionless shocks illustrating the most important features of the process with the results of a hybrid simulation of the oxygen ions heating in a quasi-perpendicular shock considered earlier by Bykov et al. 2008 - Chapter 7, this volume.

2.1. Collisionless shock heating of the ions

Ion heating mechanisms in collisionless shocks depend on the shock Alfvén Mach number, the magnetic field inclination angle (_n), plasma parameter and the composition of the incoming plasma flow. The structure of a supercritical shock is governed by the ion flows instabilities (see e.g. Kennel et al. 1985, Lembege et al. 2004, Burgess et al. 2005). In a quasi-parallel shock (_n 45°) a mixed effect of a sizeable backstreaming ion fraction and the ions scattered by the strong magnetic field fluctuations (filling the wide shock transition region) results in the heating of ions in the downstream region. The ions reflected and slowed down by an electric potential jump at the shock ramp of a quasi-perpendicular (_n 45°) shock constitute a multi-stream distribution just behind a relatively thin magnetic ramp as it is seen in Fig. 1 and Fig. 2 (left panel). The O VII phase densities and distribution functions were simulated with a hybrid code for a quasi-perpendicular (_n = 80°) shock in a hydrogen-helium dominated plasma (see Bykov et al. 2008 - Chapter 7, this volume). Phase densities x - v_x, x - v_y, x - v_z of the O VII ion are shown in Fig. 1 in the reference frame where the particle reflecting wall (at far right) is at rest and the shock is moving. The shock is propagating along the x -axis from the left to the right and the magnetic field is in the x-z plane. The system is periodic in the y dimension. The incoming plasma beam in the simulation was composed of protons (90%), alpha particles (9.9%) and a dynamically insignificant fraction of oxygen ions (O VII) with the upstream plasma parameter ~ 1. The ions do not change their initial charge states in a few gyro-periods while crossing the cosmological shock ramp where the Coulomb interactions are negligible.

Figure 1. O VII phase density in a hybrid simulated quasi-perpendicular shock (80° inclination). The shock is moving from left to right in the reference frame where the particle reflecting wall is at rest. The figures show the oxygen phase densities in x - vx, x - vy and x - vz projections from top to bottom respectively. The size of the simulation box in x-dimension is about 300 li.

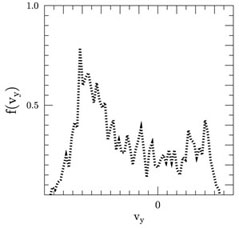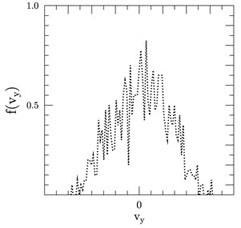Figure 2. Hybrid simulated O VII distribution function (normalised) as a function of a random velocity component vy = vy - <vy> transverse to the downstream magnetic field in a quasi-perpendicular shock (80° inclination). The shock propagates along the x-axis, while the initial regular magnetic field is in the x-z plane. In the left panel the distribution in the viscous velocity jump is shown. The right panel shows the distribution behind the jump at the position of the left end in Fig. 1. Multi-velocity structure of the flow is clearly seen in the left panel, while it is relaxing to quasi-Maxwellian in the right panel.

The simulated data in Fig. 1 show the ion velocities phase mixing resulting in a thermal-like broad ion distribution at a distance of some hundreds of ion inertial lengths in the shock downstream (see the right panel in Fig. 2). It is also clear in Fig. 1 that the shocked ion distribution tends to have anisotropy of the effective temperature. The temperature anisotropy T ~ 3 T_|| relative to the magnetic field was found in that simulation. Moreover, the hybrid simulation shows that the T of the O VII is about 25 times higher than the effective perpendicular temperature of the protons. Thus the ion downstream temperature declines from the linear dependence on the ion mass. The simulations show excessive heating of heavy ions in comparison with protons.

Lee & Wu (2000) proposed a simplified analytical model to estimate the ion perpendicular temperature dependence on Z / A, where m_i = A m_p. Specifically, the model predicts the ratio of the ion gyration velocity v_ig2 in the downstream of a perpendicular shock (_n ~ 90°) to the velocity of the incident ion in the shock upstream, v₁,

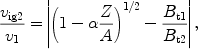where = 2 e / m_pv₁² < 1, and the potential jump is calculated in the shock normal frame (see Lee & Wu 2000). The model is valid for the ions with gyroradii larger than the shock transition width _vi. It is not a fair approximation for the protons, but it is much better for temperature estimation of heavy ions just behind the shock magnetic ramp. The model of ion heating in the fast, supercritical quasi-perpendicular (_n 45°) shocks of _a 3 predicts a higher downstream perpendicular temperature for the ions with larger A / Z.

2.2. Collisionless heating of the electrons

The initial electron temperature just behind the viscous ion jump of a cosmological shock depends on the collisionless heating of the electrons. The only direct measurements of the electron heating by collisionless shocks are those in the Heliosphere. The interplanetary shock data compiled by Schwartz et al. (1988) show a modest, though systematic departure of the electron heating from that which would result from the approximately constant ratio of the perpendicular temperature to the magnetic field strength (i.e. adiabatic heating). Thus, some modest non-adiabatic electron collisionless heating is likely present. In the case of a nonradiative supernova shock propagating through partially ionised interstellar medium the ratio T_e / T_i in a thin layer (typically < 10¹⁷ cm) just behind a shock can be tested using the optical diagnostics of broad and narrow Balmer lines (e.g. Raymond 2001). High resolution Hubble Space Telescope (HST) Supernova remant (SNR) images make that approach rather attractive. A simple scaling T_e / T_i v_sh^-2 was suggested by Ghavamian et al. (2007) to be consistent with the optical observations of SNRs.

Strong shocks are thought to transfer a sizeable fraction of the bulk kinetic energy of the flow into large amplitude nonlinear waves in the magnetic ramp region. The thermal electron velocities in the ambient medium are higher than the shock speed if the shock Mach number _s < (m_p / m_e)^1/2, allowing for a nearly-isotropic angular distribution of the electrons. Non-resonant interactions of these electrons with large-amplitude turbulent fluctuations in the shock transition region could result in collisionless heating and pre-acceleration of the electrons (Bykov & Uvarov 1999, Bykov 2005). They calculated the electron energy spectrum in the vicinity of the shock waves and showed that the heating and pre-acceleration of the electrons occur on a scale of the order of several hundred ion inertial lengths in the vicinity of the viscous discontinuity. Although the electron distribution function is in a significantly non-equilibrium state near the shock front, its low energy part can be approximated by a Maxwellian distribution. The effective electron temperature just behind the front, obtained in this manner, increases with the shock wave velocity as T_e v_sh^b with b 2. They also showed that if the electron transport in the shock transition region is due to turbulent advection by strong vortex fluctuations of the scale of about the ion inertial length, then the nonresonant electron heating is rather slow (i.e. b 0.5). The highly developed vortex-type turbulence is expected to be present in the transition regions of very strong shocks. That would imply that the initial T_e / T_i v_sh^(b-a) just behind the transition region would decrease with the shock velocity for _s >> 1. Here the index a is defined by the relation T_i v_sh^a for a strong shock. The degree of electron-ion equilibration in a collisionless shock is a declining function of shock speed. In the case of strong vortex-type turbulence in the shock transition region one expects in the standard ion heating case with a = 2 and rather small b to have (a - b) 2. That T_e / T_i scaling is somewhat flatter, but roughly consistent with, that advocated by Ghavamian et al. (2007). On the other hand in a collisionless shock of a moderate strength _s < 10 the electron transport through the magnetic ramp region could be diffusive, rather than by the turbulent advection by a strong vortexes. That results in a larger degree of the collisionless electron heating/equilibration in the shocks as it is shown in Fig. 4 of the paper by Bykov & Uvarov (1999). Recently, Markevitch & Vikhlinin (2007) argued for the collisionless heating/equilibration of the electron temperature in the bow shock of _s ~ 3 in the 1E 0657-56 cluster.

If the local Mach number _s of the incoming flow in a strong shock wave exceeds (m_p / m_e)^1/2, which could occur in the cluster accretion shocks, the thermal electron distribution becomes highly anisotropic and high frequency whistler type mode generation effects could become important. Levinson (1996) performed a detailed study of resonant electron acceleration by the whistler mode for fast MHD shock waves. Electron heating and Coulomb relaxation in the strong accretion shocks in clusters of galaxies was discussed in details by Fox & Loeb (1997).

We summarise this section concluding that a collisionless shock produces in the downstream flow a highly non-equilibrium plasma state with strongly different temperatures of the electrons and ions of different species. Moreover, the postshock ion temperatures are anisotropic. The width of the collisionless shock transition region is smaller by many orders of magnitude than the Coulomb mean free path (that is of a kiloparsec range). We consider now the structure and the processes in the postshock Coulomb equilibration layers in the WHIM.