To simulate absorption spectra of bright quasars in the intervening WHIM filaments (e.g. Kawahara et al. 2006 as an example of such a modelling) one should solve the ionisation balance equations for the charge states of metal ions with account taken of all the LTE processes and also the nonthermal particle contribution (see Porquet et al. 2001 for a discussion of a role of non-relativistic super-thermal distributions). The ionisation balance equation can be written as
 |
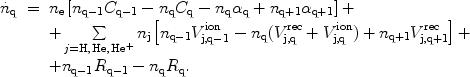Here q is the charge state of an element, Cq is
the collisional (and autoionisation) rate q
q + 1,
q are the
radiative and the dielectronic ionisation
rates q
q - 1 (in cm3 s-1),
Vj,qrec.
Vj,qion are the charge exchange rates with
the ion j (in cm3 s-1) and
Rq is the photoionisation
rate of an ion (in s-1). The rates of different processes can
be calculated for different temperature regimes (see
Kaastra et
al. 2008
- Chapter 9, this volume). We just limit our discussion here to
one example of such a simulation.
In Fig. 4 we illustrate collisional
ionisation equilibrium curves of oxygen ions in the present epoch
(at z = 0) as a function of WHIM density
. The various
boundaries separate regimes under which a certain process does, or
does not attain equilibrium over a Hubble time. We show in
Fig. 4 some critical boundaries for kinetic and
thermal equilibrium. The solid line in the upper left hand corner
labelled 'tei < tH' indicates where electron and
proton fluids reach kinetic equilibrium (proton temperature equal to
electron temperature) in a Hubble time (tH): at low density
and high temperature, such equilibrium does not attain. Low density
gas will not radiatively cool over a Hubble time to the left of the
boundaries marked 'tcool >
tH'. The cooling time
was calculated for collisionally ionised gas. The solid curve
labelled 'adiabatic evolution' indicates the locus of gas that
has only undergone adiabatic compression or expansion since high
redshift (initial condition Te ~ 104 K);
all shock-heated gas
will be above this line right after passing through a shock. The
shaded area in the upper right hand corner indicates the regime
where the collisional ionisation timescale is shorter than the
photoionisation timescale, for ionisation O VIII
O IX. The two boundaries labelled 'tcoll <
tH'
indicate where the collisional ionisation timescale becomes shorter
than the Hubble time. At lower temperature, the ionisation balance
cannot be in (collisional) equilibrium. . The steep solid curve labelled
'trec(Oxygen) > tH'
indicates where the radiative recombination timescale
(O IX O VIII)
exceeds the Hubble time since there is no recombination at low densities.
 |
Figure 4. Phase
diagram for oxygen in the IGM at redshift z = 0. Density is
parameterised by the
|
Note that we illustrate here only the collisional equilibrium case. For the more appropriate case of radiative cooling in photoionisation equilibrium, the cooling times will be even longer, due to the fact that a photoionised plasma is highly overionised compared to the characteristic ionisation- and excitation potentials, which suppresses the (very effective) collisional cooling contribution. In our figure, the lines tcool = tH will shift to the right if we calculate with the probably more realistic case of photoionisation equilibrium. However, as we argued above the collisional equilibrium is also of interest, since it represents a conservative case. The range of ionisation states of oxygen in the WHIM filaments can be observed in the absorption spectra of bright quasars.