2. ENERGETIC FEEDBACK AND STAR FORMATION

As discussed in the previous section, star formation and energetic feedback plays a dominant role in understanding the origin and evolution of galactic disks and in determining the morphological type of disk galaxies. Scannapieco et al. (2008) for example demonstrate that the same initial conditions could produce either an elliptical or a disk galaxy, depending on the adopted efficiency of gas heating during the protogalactic collapse phase. We do not yet have a consistent model of the structure and evolution of the multi-phase, turbulent interstellar medium and its condensation into stars. This situation is now improving rapidly due to more sophisticated numerical methods and fast computational platforms that allow us to run high-resolution models, incorporating a large number of possibly relevant physical processes (Wada & Norman 2002, Krumholz & McKee 2005, Tasker & Bryan 2008, Robertson & Kravtsov 2008). Most cosmological simulations however have up to know adopted simplified observationally motivated descriptions of star formation that are based on the empirical Kennicutt relations (Kennicutt 1998, 2007) that come in two different version. The first relation (K1) represents a correlation between the star formation rate per surface area _SFR and the gas surface density _g, averaged over the whole galaxy

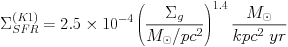(3)

The second relation (K2) includes a dependence on the typical orbital period _orb of the disk

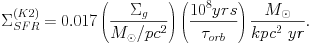(4)

These relationships have been derived from observations as an average over the whole disk. They are however often also used as theoretical prescriptions for the local star formation rate which appears observationally justified if the total gas surface densitiy _g is replaced by the local surface density of molecular gas. The origin of both relationships is not well understood yet. For example, Li et al. (2005, 2006) ran SPH simulations of a gravitationally unstable gaseous disks, confined by the gravitational potential of a surrounding dark matter halo. Gravitationally bound gas clumps form in their disks and are replaced by accreting sink particles. The authors assume that 30% of the mass of these particles is in stars with the rest remaining gaseous. However, no stellar feedback or a destruction mechanism of the partly gaseous sink particles was adopted. The star formation surface density is investigated for different galactic disk models with different rotational velocities and initial gas surface densities. The authors find a good agreement with the first Kennicutt relation (K1) if they correlate _SFR with _g at a time when the star formation rate has decreased by a factor of 2.7 with respect to the initial value which in their model typically corresponds to an evolutionary time of a few 10⁷ yrs. The significance of this result is however not clear. Obviously, the galaxies studied by Kennicutt are much older and in a phase of self-regulated star formation that cannot be considered in models without energetic feedback. In addition, the authors cannot reproduce the second relation (K2), indicating that K2 is not directly related to K1 but instead represents a second constraint for theoretical models.

We can combine K1 and K2 and derive a relationship between the average gas density in galactic disks and their orbital period

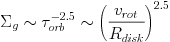(5)

where v_rot and R_disk are the rotational velocity and the size of the galactic disk, respectively. This result is puzzling as it is not clear why the kinematical properties of galactic disks should correlate with their gas surface densities especially in galaxies of Milky Way type or earlier where the gas fraction is small compared to the mass in stars. Recent detailed hydrodynamical simulations of disk galaxies by Robertson & Kravtsov (2008), including low-temperature gas cooling and molecular hydrogen physics can indeed reproduce both Kennicutt relations. The authors however note themselves that the physical reason for the origin of the K2-relation in their simulations is unclear. They argue that in disk galaxies with exponential density profiles the disk surface density should scale with the orbital period as _d ~ _orb^-2. In this case, K2 requires that _g ~ _d^1.2 ~ (_* + _g)^1.2 with _* the stellar surface density. It is not clear why this relation should hold, especially for disks with _* > _g.