Gas expands away from long-lived pressure sources like HII regions and OB association bubbles. If the expansion scale is smaller than the scale of a single cloud or the distance to a nearby cloud, then pillars and bright rims form by the push-back of interclump gas. In this case, star formation is a relatively fast process that works by squeezing the pre-existing dense gas. The velocity of the triggered stars is smaller than the overall shell expansion speed. The time delay between the beginning of the pressure source and the formation of new stars is the time for the pressure disturbance to reach the pre-existing cloud, i.e., the HII region expansion time, plus the time for the pressure to implode the cloud, which is relatively fast.
If the expansion scale is larger than the scale of a single cloud, then shells form by the push-back of most nearby gas. A cavity then forms with accumulated dense gas at the edge. This process of triggering is relatively slow because new clumps have to form by gravitational instabilities in the swept-up gas. The timescale for collapse and the properties of shells when they collapse were investigated by Elmegreen et al. (2002) using collapse criteria in Elmegreen (1994). They ran several thousand models of expanding shells in rotating, shearing galaxies and found various trends with environmental factors. The basic time scale for triggering was
 |
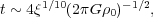(6.1) |
where ξ = 
5
/ GL for source luminosity L and sound speed
in the shell, and for
pre-shell density
0.
They also found that the probability of collapse, or
the fraction of shells that collapse, f, depends on the Toomre
Q parameter for all possible variations in environment (see
Lecture 1). The relation is f ~ 0.5- 0.4 log10 Q.
Simulations of shell formation and collapse around HII regions were
made by Hosokawa & Inutsuka
(2005,
2006a,
2006b)
and
Dale et
al. (2007a).
Hosokawa &
Inutsuka (2006a)
found that shells driven into molecular clouds at
typical densities have time to fragment and form new stars. They showed
that at low ambient densities, the fragmentation can occur before CO
forms, but at high densities, the shell is primarily CO.
Hosokawa &
Inutsuka (2006b)
considered the minimum stellar mass that drives an expansion in which
triggered star formation produces a second generation mass comparable
to or larger than the first star; this stellar mass is around
20 M
for
a pre-shock density of 100 cm-3.
Dale et
al. (2007a)
ran several simulations of an expanding HII region into a molecular
cloud and compared the resulting radii and times for collapse with the
analytical theory by
Whitworth et
al. (1994),
which represented the numerical results well.
For the collect and collapse process, the velocity of triggered stars
in the swept-up region can be large, ~ (P /
0)1/2 for
driving pressure P and ambient density
0.
Evidence for
triggering involves the causality condition: the triggering distance,
age difference, and relative velocity of the triggered stars compared
to the pressure-driving stars has to satisfy the relationship that the
distance equals the velocity times the time. The triggered stars have
to be much younger than the pressure-driving stars, and there has to be
a clear age bifurcation into triggering star ages and triggered star
ages, in order to be certain that triggering has occurred. Without a
clear age difference, the suspected triggered stars could be part of
the overall star formation process in the first generation, even if
they are located in a compressed clump near the edge of the pressurized
region.
Simulations of star formation triggered by ionization pressure have been discussed by Dale et al. (2005, 2007b) and Gritschneder et al. (2009). These simulations run for too short a time to generate an expanding coherent shell and form stars by the collect and collapse mechanism. Triggering instead is by the forced compression of pre-existing clumps. Because stars are forming in these clumps anyway, the excess star formation from triggering is small. Longer-time simulations could show more triggering in the collect and collapse scenario. As mentioned above, the timescale has to be several times the dynamical time in the pre-shock material. This is a problem for clouds that are not magnetically supported because they will collapse anyway in that time, even without compression. Thus triggering, as observed in shells, requires stability before the compression arrives, presumably from magnetic forces, and instability after the compression, presumably from enhanced magnetic diffusion in the compressed region combined with a greater surface pressure for the given cloud mass.
Thick shells should differ from thin shells in their stability properties because the gravitational forces in the shell are diluted by thickness when it is large, as discussed for galactic disks in Section 1.1 of Lecture 1. Wünsch (2010) studied the thick shell case for shells that do not accumulate material as they expand, but are bound on both sides by thermal pressure.