


After having reproduced numerically some of the extragalactic tidal structures observed in the Universe, several physical and mathematical descriptions of the phenomenon have been proposed to better understand the tides at galactic scale. The complexity of the task comes from the diversity of possible configurations, which translates into a large number of parameters. In this section, we review the role of the first order parameters and illustrate their respective effects thanks to numerical simulations of interacting galaxies. A mathematical description of the tidal field is also presented.
3.1. Gravitational potential and tidal tensor
By definition, the tides are a differential effect of the gravitation. Let's consider a galaxy, immersed in a given gravitational field. At the position of a point within the galaxy, the net acceleration can be split into the effect from the rest of the galaxy aint, and the acceleration due to external sources aext. The latter can itself be seen as a part common to the entire galaxy (usually the acceleration of the center of mass), and the differencial acceleration, that differs from point to point within the galaxy. In other terms, the net acceleration at the position rP, in the reference frame of the center of mass of the galaxy (which lies at the position rg), is given by
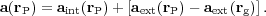 |
(1) |
For small  = rP - rg with
respect to rg, one can develop at first order and get
= rP - rg with
respect to rg, one can develop at first order and get
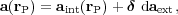 |
(2) |
which also reads
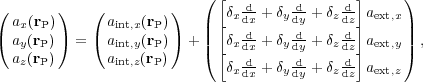 |
(3) |
or simpler
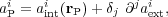 |
(4) |
when using Einstein's summation convention. The effect of the external sources on the galaxy are described by the term
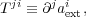 |
(5) |
which is the j,i term of the 3 × 3 tensor T called tidal tensor (Renaud et al. 2008). Such a tensor encloses all the information about the differential acceleration within the galaxy. Therefore, the (linearized) tidal field at a given point in space is described by the tensor evaluated at this point.
Note that the tidal tensor is a static representation of the tidal field: the net effect on the galaxy also depends on its orbit in the external potential, or in other words, on the variations of intensity and orientation of the tidal field. This can be accounted for by writing to pseudo-accelerations (centrifugal, Coriolis and Euler) in the co-rotating (i.e. non-inertial) reference frame, or by the means of a time-dependent effective tidal tensor in the inertial reference frame. For simplicity, in the following we focus on static, purely gravitational tides and refer the reader to Renaud et al. (2011) for more details.
Because the acceleration aext derives from a
gravitational potential
 ext, one can write
ext, one can write
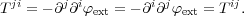 |
(6) |
(Several examples of tidal tensors of analytical density profiles are given in Renaud et al. 2009, see also the Appendix B of Renaud 2010.) It is important to note that these considerations are scale-free and applies to any spatially extended object, such as galaxy clusters, galaxies, star clusters, stars, planets, etc.
For example, let's consider the Earth-Moon system and compute the tidal field with the Moon as source of gravitation. It can been seen from the Earth as a point-mass, and yields a potential of the form
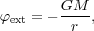 |
(7) |
with r = (xi
where
The signs of the diagonal terms (which are, in this case, the
eigenvalues because the tensor is writen in its proper base) denotes
differential forces pointing inward along the i-axis, and outward
along the other two axes. A rapid study of the differential forces
around the Earth (see Figure 5) shows indeed,
that they point toward the Earth along the axes perpendicular to the
direction of Moon. One speaks of a compressive effect. Along the
Earth-Moon axis however, the differential forces point away from the
planet: the effect is extensive.
Back to the general case, it follows from Equation 6 that any tidal
tensor is symmetric. Because it is also real-valued, it can be set in
diagonal form, by switching to its proper base. In this case, three
eigenvalues
{
which can be connected to the local density
ρ thanks to Poisson's equation:
The condition on the sign of the trace implies that it is impossible to
compute simultaneously three strictly positive eigenvalues. Remains the
cases of two, one or no positive eigenvalues, as mentioned by
Dekel et al. (2003).
For two or one positive
Note that a compressive mode (three negative
The duality of compressive/extensive tidal modes plays a role in the
formation, early evolution and dissolution rates of star clusters. It
has been noted that observed young clusters were preferentially found in
the regions of compressive tides (see
Renaud et al. 2008
in the case of the Antennae galaxies), and a compressive mode
would slow down the dissolution of young globulars
(Renaud et al. 2011).
3.3. Formation of tidal tails and bridges
In isolation, a galaxy keeps its material, which is made of dark matter,
stars, gas and dust, bound thanks to the gravitation. However, when it
moves in an external potential, created for instance by neighbor
galaxies, it can experience gravitational forces which are different
from one side of the galaxy to the other. In other words, the galaxy is
plunged in a tidal field. As a result, its material undergoes deforming
effects that re-arrange the individual components of the galaxy. On the
one hand, when this material was initially distributed in an (almost)
random way in phase-space (as opposed to e.g. sharing a common velocity
pattern), the net tidal effect does not translate into a clear global
change for an entire region of the galaxy. Therefore, such tides are
difficult to detect. On the other hand, when large scale, regular
patterns exists in the distribution of the galactic material in
phase-space (e.g. a disk), the tides have a similar impact on stars that
already lied in the same region of phase-space. All these stars are
affected the same way and thus, the effect is much more visible. In the
end, a given tidal field is easier to detect when it affects a regular,
organized distribution of matter, than when it applies to isotropic
structures. This is the reason why tidal features like tails and bridges
are well visible around disk galaxies where the motion is
well-organized, and merely inexistent in ellipticals, which yield much
more isotropic distributions of positions and velocities. This last
point can be extended to all structures with a high degree of symmetry
(halos, bulges, and so on), as opposed to axisymmetric components like
disks.
As a consequence, the tidal structures gather the matter that occupy a
well-defined region in phase-space. Figure 6
(top row) shows the N-body
toy-simulation of an encounter between a composite galaxy
(disk+bulge+dark matter halo) and a point mass. Particles being part of
one of the tails are tagged so that it is possible to track them back in
time to their initial position in the disk. As mentioned above, these
particles are distributed in a more or less confined region of
phase-space at the time of the pericenter passage of the intruder, so
that their individual motions are re-organized in a similar way. It is
interesting to note that they cover a wide range of radii in the disk
and thus, because of the differential rotation, the zone they occupy
before the interaction is far from being symmetrical.
When the same experiment is repeated with an elliptical galaxy
(Figure 6, bottom row), the velocities are
distributed almost isotropically and thus, no structure is created by
the tidal field. As a conclusion, strong galactic tidal bridges and
tails are formed from the material of disks galaxies. Note that the
experiment we conducted above applies to any mass element, and thus can
be, in principle, extended to both the gaseous and stellar components of
a galaxy.
In the case of a flyby, the galaxies do not penetrate in the densest
regions of their counterpart, do no loose enough orbital energy to
become bound to each other, and thus they escape without
merging. However, when the exchange of orbital angular momentum (through
dynamical friction) is too high, the mean distance between the
progenitors rapidly decreases (as a damped oscillation) before they
finally merge, forming a unique massive galaxy. On the external regions
of the merger, the tidal tails (if they exist) expand in the
intergalactic medium and slowly dissolve. Because the tails are
generally long-lived, they can indicate past interactions, as discussed
in
Struck (1999).
As a result, tidal features can point to interacting events, even when
what has caused their creation (i.e. a counterpart progenitor) has
disappeared in a merger or has flown away.
The response of the gas to a galactic interaction can be seen as either
an outflow or an inflow. For distant, non-violent encounters, a large
fraction of the hot gas (T > 103 K) can be tidally
ejected into the intergalactic medium, thus forming broad gaseous tails
and/or halos around galaxies (see e.g.
Kim et al. 2009).
It has been noted that while the least bound material would expand
widely, more bound structures could easily fall back into the central
region of the galaxies within less than ~ 1 Gyr
(Hibbard & Mihos
1995,
Hibbard & van
Gorkom 1996).
During a first, distant passage, some galactic material is stripped off
thanks to the transformation of the orbital energy of the progenitor
galaxies. As a result, and because of dynamical friction, the
interacting pair becomes more and more concentrated and can, under
precise conditions (see e.g.
White 1978),
experience other passage(s) and finally end as a merger
(Barnes &
Hernquist 1992a).
During such a
second, closer interaction, tidal forces can induce shocks covering a
large fraction of the galactic disk, which gives the gas a significantly
different behavior than that of the stars
(Negroponte &
White 1983).
In particular, when stellar and gaseous bars form, the symmetry of the
galaxy is broken: gravitational torques remove the angular momentum of
this gaseous structure
(Combes & Gerin
1985)
and make it fall onto the nucleus of the merger (< 1 kpc, see e.g.
Noguchi 1988,
Barnes &
Hernquist 1991,
Hernquist &
Mihos 1995,
Mihos & Hernquist
1996).
Such an inflow fuels the central region of the merger and participates
in the nuclear starburst
(Springel 2000,
Barnes 2002,
Naab et al. 2006)
often observed as an excess of infrared light or a strong nuclear activity
(Larson & Tinsley
1978,
Lonsdale et
al. 1984,
Soifer et al. 1984,
Genzel et al. 2001,
Younger et
al. 2010).
At large radii in a disk, one gets the opposite effect: the
gravitational torques push the material to the outer regions. This
outflow enhances the formation of the tails already formed by the tidal
field itself
(Bournaud 2010).
Note that star formation in mergers is also considered to be triggered
by energy dissipation through shocks
(Barnes 2004).
This is, however, quite sensible to the orbital parameters of the
galaxies. Details about merger-induced starbursts are out of the scope
of the present document. The reader can find a mine of information on
this topic in
Hopkins et
al. (2006),
Robertson et
al. (2006),
Di Matteo et
al. (2007),
Cox et al. (2008),
Hopkins et
al. (2009),
Teyssier et
al. (2010)
and references therein.
Interestingly,
Springel &
Hernquist (2005)
showed that the collision between two
gas-dominated disks could form a spiral-like galaxy instead of an
elliptical one, as one could expect. In this case, a significant
fraction of the gas is not consumed by the burst of star formation
induced by the merger. Through conservation of the angular momentum,
dissipation transforms the gaseous structure into a star-forming disk
(Hopkins et
al. 2009).
Owning that the gas fraction in galaxy increases with redshift (as
suggested by
Faber 2007,
Lotz et al. 2010),
this last point sheds light on the formation history of low-redshift
spiral galaxies.
3.5. Influence of the internal and orbital
parameters
The details on the formation of tidal structures are adjusted by several
parameters that mainly concern the orbit of the galaxies, i.e. the way
one sees the gravitational potential of the other. Because an analytical
study of the influence of these parameters is very involved, many
authors conducted numerical surveys to highlight the trends obtained
from several morphologies.
In their pioneer study,
Toomre & Toomre
(1972)
already mentioned the influence of the spin-orbit coupling of the
progenitors. For simplicity, let's consider two galaxies A and B
separated by a distance rAB, and whose disks lie in
the orbital plane. The norm of the velocity of an element of mass of the
galaxy A situated at a radius r, relative to the galaxy B is
rAB
Although this conclusion can be exported to inclined orbits, the
strongest responses of the disks are seen for planar orbits, i.e. with a
zero-inclination. The highly inclined configurations, called polar
orbits, give generally birth to a single tail, as opposed to the
bridge/tail pairs
(Howard et al. 1993).
In short, because an observed tidal effect does not only depend on the
strength of the differential forces, but also on the duration of their
existence, long tails are associated with prograde configurations.
Another key parameter is the mass ratio of the progenitors. In the
hierarchical scenario, the galaxies form through the repeated accretion
of small satellites (see e.g.
Stewart et al. 2008
and references therein), and interactions between a main galaxy and
number of smaller progenitors would occur more or less continuously. It
is usual to distinguish the major mergers where the mass ratio is
smaller than 3:1 (i.e. almost equal-mass galaxies), from the minor
mergers involving a larger ratio (e.g. 10:1). In the last case, tidal
tails are generally thin and small, while the same features are more
extended and survive for a longer time in major mergers
(Namboodiri &
Kochhar 1985).
The dependence of the structure of the remnant of the interaction (disky
or boxy elliptical, as opposed to more symmetric galaxies) on the mass
ratio of the progenitors has been extensively debated but is not
directly connected to the tidal activity, and thus is out of the scope
of this review (see
Schweizer 1982,
Barnes &
Hernquist 1991,
Barnes &
Hernquist 1992a,
Hernquist 1992,
Hernquist 1993,
Naab & Burkert
2003,
Bournaud et
al. 2005,
Bournaud et
al. 2007
for much more details).
During the interaction, the impact parameter plays an indirect role: a
close, penetrating encounter will drive one galaxy deep inside the high
density regions of the other, which implies a strong dynamical friction
(see e.g.
Bertin et al. 2003).
In this case, the separation of the progenitors after such a passage
would be much smaller than for a more distant encounter.
Furthermore, a close passage generally corresponds to a significant
tidal stripping. This situation occurs repeatedly for satellites
orbiting within the halo of major galaxies
(Read et al. 2006).
Only the densest satellites can survive such a disruption
(Seguin & Dupraz
1996),
while more fragile object would be converted into stellar streams
(Johnston et
al. 1999,
Mayer et al. 2002,
Peñarrubia
et al. 2009),
as observed in the local Universe
(Ibata et al. 2001).
However, the mass captured by a more massive companion (mass ratio close
to 1:1) seems to be higher for short pericenter distances, as noted by
Wallin & Stuart
(1992).
The lost of material into the intergalactic medium is also higher under
these circumstances.
In addition to the effect of orbital parameters, several authors noted
the role played by the dark matter halo of the progenitor on the
morphology of the merger, mainly the lenght of the tails. E.g.
Dubinski et
al. (1996)
showed that long, massive tidal tails are associated with light halos,
while the deep potential created by more massive ones would prevent the
creation of extended structures. Note that, for a given mass, a dense
halo appears to be more efficient in retaining the stellar component
bound
(Mihos et al. 1998).
An important conclusion of this work was that galaxies exhibiting
striking tails are likely to have relatively light halo (i.e. a dark to
baryonic mass ratio smaller than ~ 10:1).
However,
Springel &
White (1999)
qualified this by stating that the
important parameter is in fact the ratio of escape velocity to circular
velocity of the disk, at about solar radius (see also
Dubinski et
al. 1999).
Therefore, even massive halos (e.g. mass ratio 40:1) can allow the
growth of tails, provided the kinetic energy of the disk material is
high enough to balance the depth of the gravitational potential of the
massive dark matter halo. See Section 6.3
for more details.
3.6. Rings, ripples, shells and warps
Although they are the most visible structures formed during galactic
interactions, the tidal tails and bridges are not the only signatures of
encounters. Other mechanisms (not directly of tidal origin) lead to
disrupted morphology. We briefly mentioned them here, for the sake of
completeness.
3.7. Differences with tides at other scales
The galactic tides are a purely gravitational effect, which means that
they rely on scale-free quantities like the relative mass of the
galaxies, the inclination of the orbits, their relative velocities and
so on. Therefore, the conclusions presented above can be applied to any
scales, from planetary to cosmological. If true in principle, this
statement must be qualified because the requirements of the
galactic-type tides themselves do not exist at all scales.
In the case of planetary tides, for example in the Earth-Moon system,
the source of gravity does not penetrate in the object experiencing
tides, and is generally situated at a distance large enough that it can
be approximated by a point-mass. Furthermore, the binding energy of a
solid and/or dense body like a planet is much higher than those of the
galaxy on its stars. That is, the planetary tidal effects are weaker
than the galactic ones. Note however that both the planetary and the
galactic tides can destroy an object, like the comet Shoemaker-Levy 9
pulled apart by Jupiter's tidal field, or dwarf galaxies that dissolves
in the halo of a larger galaxy, generally forming streams.
Another major difference arises from the periodicity of the
motion. While a binary star or a planet is orbiting in a regular,
periodic way, the galaxies show more complex trajectories, highly
asymmetric, and rarely closed (because of high velocity dispersion
and/or orbital decay). As a consequence, the tides at stellar or
planetary scales can be seen as a continuous, or at least periodic
effect, while they are rather well-defined in time and never occur twice
the same way at galactic scales.
Therefore, the tidal effects seen at planetary or stellar scales, like
the deformation of the oceans, atmospheres or external stellar envelops
strongly differ from their equivalent phenomena in galaxies. At
intermediate scale, the star clusters share properties of both tidal
regimes. When orbiting an isolated galaxy, they undergo rather regular
tidal effects and can, by filling their Roche lobe, evacuate stars
through the Lagrange points. As a results, some globular clusters
exhibit tidal tails, as seen in observations and reproduced by
simulations (see e.g.
Belokurov et
al. 2006,
Fellhauer et
al. 2007,
Küpper et
al. 2010
and references therein).
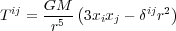
(8)
 ij = 1
if i = j and 0
otherwise. When computed at the distance d along the
i-axis (i.e. for r = d and xj =
xk = 0), the tidal tensor becomes
ij = 1
if i = j and 0
otherwise. When computed at the distance d along the
i-axis (i.e. for r = d and xj =
xk = 0), the tidal tensor becomes
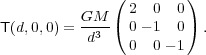
(9)
 i} denote the strength of the tides along the
associated eigenvectors. The trace of the tensor (which is
base-invariant) reads
i} denote the strength of the tides along the
associated eigenvectors. The trace of the tensor (which is
base-invariant) reads
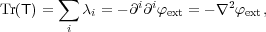
(10)
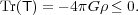
(11)
 's, the tidal field is
called
(partially) extensive, like e.g. in our Earth-Moon example. When all
three eigenvalues are negative, the tides are (fully) compressive. By
noticing that T is minus the Hessian matrix of the potential, one
can show that a change of curvature of the potential implies a change of
sign for T. Therefore, compressive tides are located in the cored
regions of potentials only, and never in cusps.
's, the tidal field is
called
(partially) extensive, like e.g. in our Earth-Moon example. When all
three eigenvalues are negative, the tides are (fully) compressive. By
noticing that T is minus the Hessian matrix of the potential, one
can show that a change of curvature of the potential implies a change of
sign for T. Therefore, compressive tides are located in the cored
regions of potentials only, and never in cusps.
 's) implies that
the local density due to the source of gravitation is non-zero. Although
such a situation does not exist with point-masses, it can occurs when
considering extended mass distributions, like e.g. for galaxies embedded
in a dark matter halo.
's) implies that
the local density due to the source of gravitation is non-zero. Although
such a situation does not exist with point-masses, it can occurs when
considering extended mass distributions, like e.g. for galaxies embedded
in a dark matter halo.
 ∓ r
∓ r
 , where
, where
 denotes orbital rotational velocity and
denotes orbital rotational velocity and
 the (internal) rotation
speed of the galaxy A (i.e. the spin). The sign of the second term
depends on the alignment of
the (internal) rotation
speed of the galaxy A (i.e. the spin). The sign of the second term
depends on the alignment of
 with
with
 . For a prograde
encounter, the spin (
. For a prograde
encounter, the spin ( )
and the orbital motion
(
)
and the orbital motion
( ) are
coupled (i.e. aligned). Therefore, the relative velocity is lower
(rAB
) are
coupled (i.e. aligned). Therefore, the relative velocity is lower
(rAB
 -
r
-
r  ) than for a
retrograde encounter (rAB
) than for a
retrograde encounter (rAB
 +
r
+
r  )
and the net effect of the tides is seen for a longer period of time. As
a result, the structures formed during prograde encounters are much more
extended than those of retrograde passages.
)
and the net effect of the tides is seen for a longer period of time. As
a result, the structures formed during prograde encounters are much more
extended than those of retrograde passages.