The consequences of feedback for the global ISM can be evaluated quantitatively in terms of the interstellar porosity parameter Q, which is the ratio: (total area or volume occupied by superbubbles) / (total area or volume of the galaxy). Thus it is essentially the filling factor of hot gas, assuming hot gas is contained within all of the superbubbles. Values of Q near unity indicate the HIM dominates the multiphase ISM, and values ≫ 1 imply an outflow, with the galaxy generating more hot gas than it can contain.
It is straightforward to use the analytic expression for N(R)
(equation 3) to derive Q in terms of a galaxy's star-formation rate,
(Oey et al. 2001;
see also
Clarke & Oey 2002):
 |
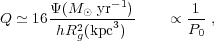(6) |
for 
= 2, a
Salpeter (1955)
IMF for stellar masses 0.1 
m 100
M
, and
P0 / k = 9500. Rg and
h are the radius of the gaseous star-forming disk and gas scale
height, respectively. We caution that Q depends on ambient
interstellar parameters, for example, P0-1
as indicated.
Oey et al. (2001)
estimated Q for all the galaxies in the Local
Group. The Milky Way yields Q ~ 1 for some methods and Q
< 1 for others, consistent with the ambiguous results found in the past
(e.g.,
McKee & Ostriker 1977;
Slavin & Cox 1993).
The LMC yields Q ~ 1, implying that hot gas
dominates the ISM volume. The remainder of the Local Group
galaxies all show Q ≪ 1, with the sole exception of IC 10, a
starburst galaxy for which Q ~ 20, thereby unambiguously
predicting an outflow.
Oey et al. (2001)
crudely estimate the mass-loss rate in this outflow
out,
assuming that the material is largely evaporated from shell walls by
thermal conduction. We find that
out ~
; indeed,
absorption-line studies of local starburst galaxies by
Heckman et al. (2000)
also show that empirically, the outflow and star-formation rates have
the same order of maagnitude for that sample.
Since Q ~ 1 represents a rough threshold for the escape of superwinds from the galactic disk, this also implies the simultaneous escape of newly-synthesized metals, which are contained in the hot gas. Likewise, the shredding of the ISM into filaments facilitates the escape of ionizing radiation, thus Q ~ 1 also represents an escape threshold for ionizing photons (Clarke & Oey 2002). We finally note the extensive body of numerical work on superbubbles and blowout conditions. Mac Low (1999) and Strickland & Stevens (2000) provide overviews of this field. The details of the numerical predictions are presently difficult to confirm empirically, but observations with XMM-Newton and Chandra are beginning to constrain the dominant processes.