5. THE INITIAL MASS FUNCTION

Once the stars are born, a mass distribution must be assumed. In fact, the chemical and mechanical feedback of massive stars substantially differ from the feedback of low-and intermediate-mass stars (see next subsections), thus it is crucial to know how many stars are formed per each mass bin. Actually, the IMF is often combined with the SFR to obtain the so-called birthrate function B(m, t) [312, 174], which gives the number of stars formed per unit stellar mass and per unit time. Usually, the time dependence is described by the SFR, whereas the mass dependence is determined by the IMF. However, one should already point out that, according to some lines of evidence, the IMF could depend on time, too (see below).

The IMF (m) was originally defined by Salpeter [242] as the number of stars per unit logarithmic mass that have formed within a specific stellar system. Thus, the total mass of stars with masses between m and m + dm is (m)dm. A very useful concept is also the IMF in number (m), giving the number of stars in the interval [m, m + dm]. Clearly, (m) = m(m). Salpeter found out that (m) m^-1.35 for 0.4 M < m < 10 M. This estimate has been refined over the years [312, 246, 130, 45] and nowadays a commonly used parametrisation is the so-called Kroupa IMF [129], namely a three-part power law (m) m^- with = -0.7 in the interval 0.01 M < m < 0.08 M (i.e. in the brown dwarf domain), = 0.3 for 0.08 M < m < 0.5 M, and finally = 1.3 (very similar to the Salpeter slope) for stellar masses larger than 0.5 M.

The paper of Romano et al. [238] clearly shows how different IMFs can change the fraction of stars in various mass bins (see their table 1). IMFs predicting smaller fractions of massive stars produce less -elements, because these elements are mainly synthesised by SNeII. This is evident in fig. 6 of [238], which shows the evolution of [ / Fe] vs. [Fe/H] for model galaxies characterised by different IMFs. Since more massive stars means more SNeII, clearly the IMF affects the energetics of a galaxy, too. This has been shown in many simulations [317, 253, 304, 343]. In particular, flat IMFs tend to produce higher fractions of massive stars and, hence, larger SNeII luminosities. The energy supplied by SNeII could be enough to unbind a fraction of the ISM and produce a galactic wind (see also Sect. 9).

It is important to point out that, usually, numerical simulations adopt a fixed value for the IMF upper stellar mass m_up, irrespective of how much gas has been converted into stars. However, m_up should depend on the mass of the newly formed stellar particles, for the simple reason that only massive star clusters can host very massive stars. A correlation between the stellar cluster mass M_cl and the upper stellar mass is indeed observationally established and can be reproduced by simply assuming that m_up is the mass for which the IMF in number (m) is equal to 1 [131]. Weidner & Kroupa [337] found that the theoretically derived M_cl - m_up relation nicely reproduces the available observations (their figs. 7 and 8; see also [340]). Clearly, this assumption can greatly affect the outcomes of simulations, but, to the best of my knowledge, it has never been explored in detail in hydrodynamical simulations of galaxies.

Since a correlation between the most massive cluster in a galaxy and the SFR is also observationally established [338], the logical consequence is that the galaxy-wide IMF in a galaxy must depend on the SFR, too. In particular, the IMF is time-dependent and is given by the integral of the IMFs of single star cluster, which are assumed to always be a Kroupa IMF, but with different upper masses m_up, depending on the star cluster mass. An upper cluster mass limit depending on is then assumed. Given a mass distribution of embedded clusters _cl(M_cl) (giving the number of star clusters in the interval [M_cl, M_cl + dM_cl]), the global, galactic-scale IMF (integrated galactic IMF or IGIMF) is given by:

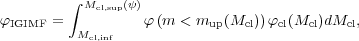(7)

(see [131, 336, 220] for details. Notice also that in the original papers the IMF in number is designed with instead of with ). The IGIMF turns out to be steeper than the Kroupa IMF assumed in each star cluster and the difference is particularly significant for low values of the SFR. Notice however that the IMF tends to become top-heavy when the SFR is very high [339]. The effect of the IGIMF on the chemical evolution of galaxies has been already explored in a few papers [125, 220, 42, 221]. It turns out that the IGIMF is a viable explanation of the low metallicity [125] or of the low / Fe ratios [220] observed in DGs. The main reason is that DGs have on average lower SFRs and this, in turn, implies steeper IMFs, characterised by a lower fraction of massive stars. The production of metals and, in particular, of -elements, is considerably reduced.

Chemo-dynamical simulations of galaxies can give a more complete picture of the evolution of DGs and of the effect of the IMF (and of the IGIMF, in particular). Fig. 1 shows the comparison of the results of two chemo-dynamical simulations, with and without adopting the IGIMF. Methods, assumptions and initial conditions are taken from [228]. In particular, the main structural properties of the shown model galaxies resemble the blue compact DG I Zw 18 (see [330, 207] for a summary of observed properties of this galaxy). The SFH is shown in the upper left panel. This particular dependence of the SFR with time has been chosen again in agreement with the reconstructed SFH of I Zw 18 as derived by [4] (but see [6] for a more recent determination of the SFH in I Zw 18). According to this SFH, the IGIMF predicts variations of the upper stellar mass and of the average IMF slope as shown in the middle and lower panels, respectively.

Figure 1. The effect of the IMF on the evolution of galaxies. left) The adopted SFR (upper panel), together with the upper stellar mass Mup (in M, middle panel) and the average slope of the IMF (in number, lower panel) calculated for the IGIMF galactic model (red lines in the right panels). right) Predicted evolution of abundances and abundance ratios for a IGIMF galactic model (red lines). Plotted are the evolution of oxygen (upper panel), carbon-to-oxygen ratio (middle panel) and nitrogen-to-oxygen ratio (lower panel). The black line represents the evolution of a model with a time-independent Salpeter IMF (i.e. with a slope of -2.35).

The evolution of gas-phase abundances and abundance ratios in a simulation adopting these IGIMF prescriptions is shown in the right panels (red lines) and compared with the results obtained with a model adopting a standard, time-independent Salpeter IMF (black lines). Since the IGIMF is steeper (and poorer in massive stars) than the Salpeter IMF, the initial phases are characterised by a lower production of oxygen and, consequently, higher values of C/O and N/O. However, due to the higher feedback, the model with Salpeter IMF experiences a galactic wind at t 120 Myr. Since galactic winds tend to be metal-enriched (see also Sect. 9), the onset of the galactic wind is characterised by a decrease in O/H. The galactic wind does not occur in the IGIMF run due to the reduced number of SNeII. At t 280 Myr a burst of star formation occurs (see upper left panel). In the Salpeter IMF run, most of the freshly produced metals are channelled out of the galaxy and do not contribute to the chemical enrichment. In the IGIMF run instead, the metals newly synthesised during the burst do contribute to the chemical enrichment and this causes a sudden increase of the oxygen abundance (and a sudden decrease of C/O and N/O). More detailed simulations, exploring wider parameter spaces, can show other effects of the IGIMF. In particular, the simulations shown in Fig. 1 assume a pre-defined SFH, but it is clear that the adoption of the IGIMF can affect the onset of the star formation, too, because it affects the energetics of the ISM. Numerical simulations of galaxies with IGIMF and with star formation recipes as described in Sect. 4 would surely predict different SFHs as compared with models with SFR-independent IMFs. This has been shown already in chemical evolution models [42] but this effect can be even more dramatic in chemo-dynamical simulations.

It is also important to point out that, in Eq. 7, only the global, galactic-scale SFR is required to calculate the IGIMF. However, the star formation process is usually very inhomogeneous within a galaxy, with regions of very enhanced star formation. Clearly, the formation of massive stars is more likely in regions of high star formation density. It is reasonable thus to expect that the IMF varies not only with time, but also with location within a galaxy. This approach has been used for instance by Pflamm-Altenburg et al. [212] to explain the cut-off in H radiation in the external regions of spiral galaxies (where the SFRs are milder). Observational evidence of the variation of the IMF within galaxies is given by Dutton et al. [69]. To finish, several lines of evidence point towards a dependence of the IMF on the metallicity, too [168, 132], in the sense that the IMF appears to become top-heavy in metal-poor environments. Clearly, the chemo-dynamical simulations of galaxies with spatially and temporally variable IMFs can give us new, different perspectives and insights to understand the evolution of galaxies.