


Bars are the most important drivers for secular evolution in galactic disks; we will see them again and again throughout this School. For this reason, I now want to give you a heuristic introduction to bar dynamics and evolution. Lia Athanassoula (2012) will talk about this subject in more detail. Here, I concentrate on a simple version of the essential physics that you need to understand in order to have an intuitive feel for how bars form, grow and die. Bars are density waves in the disk. That is, the bar pattern rotates more-or-less rigidly at a single pattern angular velocity Ωp, whereas the angular velocity Ω(r) of material in the disk varies with radius. This is even more true of spiral structure: over most of a global spiral pattern, the stars and gas have Ω > Ωp; they catch up to the spiral arms from behind, move through them in the rotation direction (lingering in the arms to give them their density enhancement) and then move on in the rotation direction toward the next arm. Since bars and spirals have some similarities, I briefly discuss spiral structure, too.
4.1. Orbital resonances in a galactic disk
Orbital resonances are the key to understanding bars and spirals. The main resonances – inner Lindblad resonance, corotation, and outer Lindblad resonance – will recur in many of the lectures at this school. I therefore need to introduce them in some detail.
The general orbit of a star in a galactic disk is an unclosed rosette, because the potential is not Keplerian (that is, the galaxy mass is distributed in radius and not all in one central point as in, for example, the Solar System).
Figure 10 shows disk orbits as seen in a frame of reference that rotates clockwise (orange arrow) at the pattern speed Ωp of some coherent structure. In this figure, I show a spiral arm (red), because spirals almost always trail in the rotation direction (that is, the arm is convex in the direction of rotation). Thus it is easy to remember the rotation direction at a glance. I work in the epicyclic approximation (Mihalas & Routly 1968; Binney & Tremaine 1987) in which radial excursions are small. Then, at the radius where the stars and the pattern corotate, i. e., where Ωp = Ω (green), a stellar orbit is a small elliptical epicycle around the mean radius. The motion around the ellipse is counterclockwise, because the forward velocity is higher when the star is closer to the center than average. In the epicyclic approximation, the motion around the ellipse is simple harmonic. Corotation is the most important resonance in the galaxy, because the mean position of the star with respect to the global pattern never changes as long as Ωp is fixed.
We will need the "epicyclic frequency" κ of the small radial and azimuthal excursions around the mean motion,
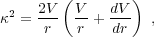 |
(3) |
where V(r) is the rotation velocity as a function of radius r.
If we move slightly inward from corotation toward the galactic center, then a star oscillates around almost-closed ellipses while drifting forward with respect to the global pattern (leftmost orbit illustrated in Fig. 10).
Contining toward smaller radii (next three orbits inward in Fig. 10), the forward drift gets faster until the backward loop disappears and we end up with an unclosed rosette orbit that involves somewhat more than two radial excursions for every revolution forward in the rotation direction around the center. It is clear that, as we move farther inward and the forward drift rate continues to increase, the orbit again becomes almost closed, now with almost exactly two radial excursions for every revolution (this is the second-innermost orbit shown in the figure).
Continuing toward still-smaller r, we arrive at "inner Lindblad resonance" (ILR) where the (blue) orbit is closed and the star executes exactly two radial excursions while it drifts forward with respect to the global pattern by one complete revolution around the center. This happens where Ωp = Ω - κ/2. ILR is again an important resonance, because the star repeatedly has the same phase in its radial oscillation when it has the same position with respect to the global pattern. So the star interacts more strongly with the pattern near ILR than it does elsewhere in the disk. Moreover, ILR gives us a first-order understanding of bar dynamics, as discussed in the next section.
Starting at corotation and moving outward, stars drift backward with respect to the global pattern as seen in our rotating frame. At some large r, the orbit is closed as the star makes two radial oscillations for every revolution backward around the center (the orbit is not illustrated). This is "outer Lindblad resonance" (OLR), and it happens where Ωp = Ω + κ/2.
The generic rotation curve V(r) and frequencies Ω(r) and Ω(r) - κ(r)/2 are shown in Fig. 3. Where V ∝ r, κ = 2 Ω and Ω - κ/2 = 0. Where V = constant, κ = √2 Ω and Ω - κ/2 = (1 - 1/√2) Ω decreases proportional to Ω. In between, Ω - κ/2 first rises and then falls with increasing r as the rotation curve turns downward from V ∝ r to V ≃ constant. The radial range over which Ω - κ/2 varies little with radius turns out to be crucial to the formation of bars and spiral arms. The evolving height and radial extent of the Ω - κ/2 maximum proves to control the fate of bars. And the natural pattern speed for bars proves to be Ωp ≃ Ω - κ/2. As follows:
4.2. Bars and spirals as almost-kinematic density waves
The essential insight into the dynamics of bars and global spirals is due to Lindblad (1956) and Kalnajs (1973; see Toomre 1977b for a lucid review). It is illustrated in Fig. 11. Especially for outward-rising rotation curves (M 33) and even for nearly constant or falling rotation curves (M 81), the angular precession rate Ω - κ/2 of ILR orbits is small and nearly constant over much of the galaxy. Suppose that Ω - κ/2 is exactly constant with r. Then: If closed ILR orbits are arranged to produce a trailing spiral enhancement in density (top left) or a straight bar (top right), the orbits will precess together at exactly the same Ω - κ/2 and so will preserve the spiral or bar shape. These are purely kinematic density waves.
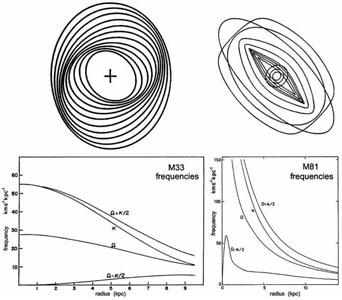 |
Figure 11. (bottom) Frequencies Ω, κ and Ω ± κ/2 for almost-circular orbits in M 33 (Shu et al. 1971) and M 81 (Visser 1980). Both galaxies have large radial ranges in which Ω - κ/2 ≃ constant and ILR orbits precess almost together. (top left) From Kalnajs (1973), elliptical ILR orbits aligned to produce a spiral density wave. (top right) From Englmaier & Gerhard (1997), examples of principal orbit families for a bar oriented at -45°. The elongated orbits parallel to the bar are the x1 family out of which the bar is constructed. If Ω - κ/2 = constant with radius over the extent of the x1 orbits, they precess together and preserve the bar shape. Interior to ILR, the x2 orbits are perpendicular to the bar. (The almost-square orbit has four radial oscillations for each revolution; it is a 4:1 ultraharmonic resonance orbit.) |
In practice, Ω - κ/2 is not quite constant. To make real bars or spirals, it is the job of self-gravity to keep the orbits precessing exactly together.
This discussion is a heuristic argument for another important conclusion. The natural pattern speed of a bar or global spiral is Ωp ≃ Ω - κ/2. Note in Fig. 11 that this is much slower than Ω over most of the galaxy. That is, stars and gas revolve around the galactic center more quickly than the pattern rotates; they catch up to the pattern from behind, participate in it for a time – lingering in the pattern and thereby enhancing its density (Toomre 1981) – and then continue onward in the forward rotation direction. For bars, corotation happens near the end of the bar or slightly beyond it (see Sellwood & Wilkinson 1993 for a review).
Some barred galaxies that have substantial (pseudo)bulges also have nuclear bars ~ one-tenth of the radius of the main bar (Section 5.2.8). When the galaxy mass distribution is very centrally concentrated, Ω - κ/2 has a high maximum at small radii (frequency curves for M 81 in Fig. 11). The natural pattern speed of a nuclear bar is roughly equal to the local value of Ω - κ/2 and is therefore much higher than the pattern speed of the main bar. This is seen in numerical simulations (Debattista & Shen 2007; Shen & Debattista 2009) and in real galaxies (Corsini et al. 2003).
The x1 family of closed bar orbits shown in Fig. 11 and the similar, non-periodic orbits that are trapped around them by the bar's self-gravity involve large perturbations from circular orbits. Strong bars are nonlinear. Then the approximations that we have made are not accurate. In particular, the true pattern speed is rather larger than the local value of Ω - κ/2 (e. g., Shen & Debattista 2009). Nevertheless, the epicyclic approximation still captures the essence of the physics (Ceverino & Klypin 2007).
In particular, for any realistic Ωp ~ Ω - κ/2, there must be an inner Lindblad resonance in a centrally concentrated galaxy such as M 81, but there cannot be an ILR in a pure-disk galaxy such as M 33. Inside ILR, the closed "x2 orbits" are elongated perpendicular to the bar (Fig. 11). So they cannot be used to construct the bar and to maintain its self-gravity. We will see in Section 5 that the secular evolution of a barred galaxy is in part to transport gas toward the center and thereby to build a pseudobulge. As secular evolution increases the central concentration of a barred galaxy, the inner maximum in Ω - κ/2 gets higher and wider in radius. Therefore it gets more difficult for self-gravity to keep the decreasing number of x1 orbits precessing together. Also, the number of (damaging) x2 orbits increases. The bar gets weaker. Thus, bars naturally commit suicide by the secular evolution that they drive. This happens preferentially in early-type galaxies, not in galaxies such as M 33. All of these heuristic predictions prove to be accurate.
4.3. The growth, structural evolution and death of bars
This section is an overview of the life histories of bars – from rapid growth through secular evolution in "middle age" through eventual death – at the level that we need in this Winter School. I concentrate in this section on the bars themselves; the effects of bars on the other components in their galaxies will be the subject of later sections. I will not cover the rich dynamics of bars in their nonlinear phases. For this work, the best review is Sellwood & Wilkinson (1993). Contact between the complicated nonlinear dynamics that is reviewed there and the simplified story that I tell here is not always good. That's where the frontier in this subject lies. Here, I will summarize the most important bar evolution processes based on a series of seminal papers. Sellwood & Wilkinson (1993, hereafter SW93) provide more references, and Athanassoula (2012) reviews – and, indeed, advances – some of these subjects in her lectures at this School.
My orientation is a little different from that of SW93. They take – as much as possible, in this complicated subject – a formal approach rooted in the rigorous mathematics of galaxy dynamics. I take an observer's approach. That is, I try to benefit as much as possible from the insight gained from analytical and n-body studies, but I also put equal emphasis on letting the observations suggest (or, in some cases, prove) which processes are at work. Sometimes observations hint that a process (e. g., evolution of bars to lenses) takes place even when the theory of such a process is not well formulated. But asking the right question is the efficient road to progress. So this observational guidance is very useful. One key is to remember which ideas are hypotheses and which are proven. And it is especially important not to overinterpret the temptingly rich array of possibilities that are inherent in this subject. I will try to be clear about the confidence with which various ideas are suggested. And I will emphasize what I believe are the most important remaining problems.
Massive, cold, rotating disks are famously unstable to the formation of bars (e. g., Ostriker & Peebles 1973; Toomre 1977b, 1981; SW93). Many n-body studies start with a stellar disk that is highly unstable and then follow the evolution of the bar that results. Most results that are derived in this way are probably realistic, modulo (important!) the neglect of gas and dark matter. However, it is important to realize that bar evolution almost certainly does not start this way. It is unrealistic to think that a disk grows axisymmetrically to a high mass, meanwhile using up its gas to make stars, and only then discovers ("Oh, my God!") that it is bar-unstable.
In a paper entitled "Most Real Bars are Not Made by the Bar Instability", Sellwood (2000) expresses a related worry. Most barred galaxies have enough central mass concentration so the bar essentially must have an ILR. That is, Ω - κ/2 is similar to the curve for M 81 in Fig. 11. Our heuristic arguments in Section 4.2 then make plausible the result that also emerges from more detailed studies (e. g., Toomre 1981), namely that a bar instability never gets started when the resulting bar would have a strong ILR. Sellwood acknowledges and dismisses the possibility that the disk might not originally have allowed an ILR, i. e., that the central concentration was manufactured by the bar only after it formed. One piece of supporting evidence was a conclusion (Abraham et al. 1999) that strongly barred galaxies were rare at z > 0.5; this is now known to be incorrect (Jogee et al. 2004). More immediate was the concern that building up the central concentration weakens the bar. I will suggest below that bar suicide happens, and it happens at a measurable (pseudo)bulge-to-disk ratio. But I, too, have worried about why strong bars can coexist with strong ILRs. The evidence will suggest that, when the central mass grows slowly while the bar has a strong angular momentum sink, a nonlinear bar can – for a while – continue to grow even when it already has an ILR. But the more important point for the present section is this: present disk conditions do not favor the growth of bars by a simple instability.
Possible implications:
Bar formation may be a threshold process that begins and then proceeds slowly and perhaps episodically (Sellwood 2000) as the disk grows massive enough with respect to its dark halo (see also Mihos et al. 1997).
The formation of the stars
that now make up the bars in early-type galaxies happened long
ago in progenitor galaxies about which we know very little. E. g., the
boxy bulge ≡ almost-end-on bar of our Galaxy is made of stars that
are very old and enhanced in α elements (see
Renzini 1999
for a review). So its stars formed over a period of
 1 Gyr. Gas
fractions were much higher then than they are now
(Genzel et al. 2006).
Gas may be centrally important to bar formation. Observations of
high-redshift disks that are nevertheless younger than our Galaxy's
bulge stars show surprises such as ~ 108 -
M⊙ clumps and high velocity dispersions
(Genzel et al.
2006;
Förster Schreiber
et al. 2009).
The clumps are believed to form by violent instabilities, and they
eventually merge to form at least some classical bulges
(Elmegreen et
al. 2008;
Section 8.1 here). None of this sounds
like the typical initial conditions assumed in n-body simulations
of bar formation. We have no reason to be confident that we know how to
start those simulations with realistic initial conditions.
1 Gyr. Gas
fractions were much higher then than they are now
(Genzel et al. 2006).
Gas may be centrally important to bar formation. Observations of
high-redshift disks that are nevertheless younger than our Galaxy's
bulge stars show surprises such as ~ 108 -
M⊙ clumps and high velocity dispersions
(Genzel et al.
2006;
Förster Schreiber
et al. 2009).
The clumps are believed to form by violent instabilities, and they
eventually merge to form at least some classical bulges
(Elmegreen et
al. 2008;
Section 8.1 here). None of this sounds
like the typical initial conditions assumed in n-body simulations
of bar formation. We have no reason to be confident that we know how to
start those simulations with realistic initial conditions.
Contrariwise, a bar may form long after star formation makes the stellar disk. One way is thought to be through tidal tickling by neighboring galaxies (e. g., Noguchi 1987, 1988; 1996, which also discusses gas infall; Gerin et al. 1990; Barnes et al. 1991; Mihos et al. 1997). It is difficult to test this (for example) by looking for an excess of barred galaxies in dense environments such as the Coma cluster. The reason is that any extra tendency to form bars where there are many galaxy encounters must compete with and may lose out to the stabilizing effects of disk heating (Marinova et al. 2012; see Kormendy & Bender 2012 for evidence that disk heating happens even in the Virgo cluster).
Occam's razor is a dangerous weapon. Answers are not guaranteed to be simple. All the above – i. e., a series of episodic, encounter-driven growth spurts that punctuate a steady, slower growth by outward angular momentum transport as envisaged by Sellwood (2000) – may happen. It is important to understand that global spiral structure connected with a bar or inner ring is a signature of outward angular momentum transport and therefore a sign that the bar is growing stronger.
In the next sections, I review the life histories of bars and the evolution that they drive in their host galaxies, keeping the above issues in mind. As needed, I emphasize where simulations do not yet include important physics. Limitations include (1) that many simulations do not include gas, and gas physics is variously but always importantly simplified, (2) that continued infall of gas and small galaxies is not included, (3) that feedback from hot young stars, from supernovae and from active galactic nuclei is generally not included and may be important, and especially (4) that simulated galaxies are usually not as multicomponent as real galaxies. Two-body relaxation is uninterestingly slow in galaxy disks. Evolution is driven by the interactions of stars and gas with collective phenomena. Physical morphology (Section 3.4) invites us to investigate the interactions of different nonaxisymmetric components in galaxies. This is where the action is.
Among the many published n-body studies of bar formation (SW93), I focus on Sparke & Sellwood (1987), because they analyze their simulation in ways that tell us what we need to know. The initial condition is an axisymmetric galaxy with a bulge-to-total ratio of 0.3. The bulge is a rigid Plummer (1911) sphere with size ~ 1/5 that of the disk. A rigid potential is a limitation: the bulge gives the galaxy an ILR, and it is interesting to see the (surprising lack of) consequences, but the bar and bulge cannot interact. The disk is a Kuz'min (1956) – Toomre (1963) model, density ∝ 1 / (a2 + r2)3/2, where r is radius and a measures the scale length of the density falloff. With a Toomre (1964) axisymmetric stability parameter of Q = 1, the initial disk was very unstable. The disk contained 50,000 particles whose gravity was softened on a length scale of 0.1 a. Other limitations are that the model contains no gas and no "live" dark matter halo of simulated particles; both of these limit the extent to which the bar sees a sink for angular momentum that allows it to grow. More detailed simulations can now be run, but this subject does not get the attention that it deserves, and in particular, analyses are not usually as physically motivated and compelling as the one in Sparke & Sellwood (1987). There is much to be learned from this simulation, as follows.
Figure 12 shows the evolution of the disk density, and Fig. 13 shows the growth in amplitude of the bar and the evolution of the pattern speed of the bar and its associated spiral structure. Time is measured in natural units (discussed in Sparke & Sellwood 1987). Beginning immediately and extending to time 50, the disk rapidly grows a two-armed instability that is bar-shaped near the center and a global, two-armed spiral farther out. The bar rapidly grows stronger: more stars participate, the axial ratio of the bar decreases, the bar grows longer and its pattern speed decreases. Figure 13 dramatically reveals the important result that the pattern speed of the bar is larger than the pattern speed of the spiral at all times. This is consistent with our heuristic argument: the bulge creates a near-central maximum in Ω - κ/2, and the pattern speeds of the bar at relatively small radii and the spiral at relatively larger radii are comparable to but slightly larger than the local value of Ω - κ/2. (Note: in Fig. 13, frequency = 2Ωp, because the pattern is bisymmetric.) Because Ωp is smaller for the spiral than for the bar, the spiral continually shears away from the bar. It is no surprise that spiral arms do not necessarily start at the end of the bar, especially in galaxies such as NGC 2523, which have well developed inner rings and which therefore are dynamically mature.
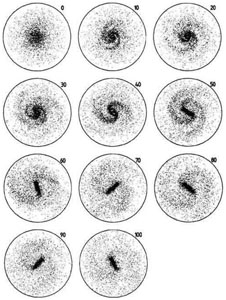 |
Figure 12. Bar formation in the n-body simulation of Sparke & Sellwood (1987, Fig. 1). Times are in natural units that are discussed in their paper. Only one particle in ten is included, and the bulge component is not shown. |
Figure 13 makes it clear that the rapid, instability-driven initial growth of the bar is followed by a distinct later phase of secular growth, when the bar amplitude increases and Ωp decreases more slowly than in the early, rapid phase. In this collisionless model, the outer disk has been heated so much that the spiral structure is weak during the secular phase (Fig. 12). In real galaxies, there are two reasons why the later growth is more dramatic. First, galaxies contain gas; (1) its response is stronger than that of the stars and, in fact, dissipative, and (2) gas also keeps the stellar disk cooler and more responsive, because the stars that form from it are formed with low velocity dispersions. Second, the dark halo in a real galaxy provides an additional sink for the disk angular momentum.
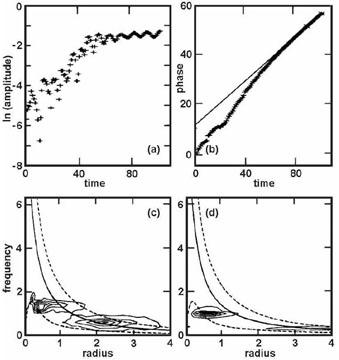 |
Figure 13. Evolution of the bar in the n-body model of Sparke & Sellwood (1987). Panels (a) and (b) show the amplitude and phase of the bar as a function of time. A straight line is fitted to the phases at late times. It shows that the pattern speed decreases quickly during the early, rapid growth of the bar and then more slowly during the later, secular growth. The bottom panels show contours of the square root of the power in the bar or spiral perturbation as a function of frequency = 2Ωp and radius. Panel (c) is for the early part of the rapid growth (up to time 31) and panel (d) is for the slow growth phase at times 40 to 103. A very important conclusion is that the bar has a higher pattern speed than the spiral structure. Also, note that the pattern speeds of both the bar and the spiral arms decrease with time, as shown for the bar in panel (b). The smooth curves show 2 Ω (solid curve) and 2 Ω ± κ (dashed curves) for the initial, axisymmetric model. They apply only approximately during the later, nonlinear phases. Nevertheless, it is clear that both the bar and the spiral have pattern speeds that are similar to but slightly larger than the local values of Ω - κ/2. Also note that the bar develops despite the fact that it has an ILR. These are Figs. 2 and 3 from Sparke & Sellwood (1987). Similar results are illustrated in Bournaud & Combes (2002). |
The bar ends roughly at corotation. Therefore, stars stream through the bar density wave in the forward direction. Analysis of the orbital structure of the late-stage model shows that – as expected – the bar is made almost exclusively of orbits trapped around the x1 family of closed orbits that align with the bar. Despite the presence of an IRL,, there are almost no orbits analogous to the x2 family (the model has only 50,000 particles, and not all orbits were checked.) Additional details of the orbit structure are discussed in Sparke & Sellwood (1987).
Comparison to real SB0 galaxies shows that the n-body bar model of Sparke & Sellwood (1987) is realistic in many respects. It has the shallow density gradient and sharp outer edge of real bars in early-type galaxies. It has the rectangular shape observed, e. g., in NGC 936 (Fig. 14). And it shows qualitatively similar non-circular streaming motions. At the end of the simulation, the disk is too hot to allow much spiral structure; therefore, the bar has no "live" component with which it can effectively interact, and as a result, it is very robust. The situation in NGC 936 is similar: the Toomre (1964) stability parameter in the outer disk is Q ≃ 3 to 4, so essentially no small-scale structure is possible (Kormendy 1984b). Not surprisingly, the purely stellar-dynamical n-body model of Sparke & Sellwood (1987) is a realistic simulation of an SB0 galaxy but not of a gas-rich barred spiral.
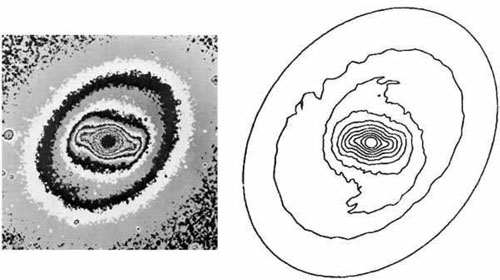 |
Figure 14. Comparison of the n-body bar model of Sparke & Sellwood (1987: isodensity contours at right) with the SB0 galaxy NGC 936 (Kormendy 1983: isophote map at left). This is Fig. 6 from Sparke & Sellwood (1987). |
Shortcomings of the model are easily linked to limitations in the physics:
The model is two-dimensional and therefore cannot include orbital complexity (including chaos) that is fundamentally three-dimensional. In particular, the bar cannot buckle and hence thicken in the axial direction (Section 4.3.3).
The lack of gas means that the model can simulate SB0 but not spiral galaxies.
The bar cannot grow very much at late times because the disk gets too hot. The same problem is well known in the context of understanding spiral structure. Quoting Toomre (1990): "The gravitational forces involved in [spiral structure] have the unwelcome side effect that they tend to increase the mean epicyclic motions of any stars ... which take part. Typically, in just a few revolutions, these would-be participants become simply too `hot' to contribute appreciably to any more fun. In other words, the vigor of these apparent `spiral instabilities' was quickly recognized to doom any hopes for their longevity – unless one adds some form of cooling ... such as might be natural in a gas but surely not in a disk of stars." Toomre concluded that "It really seems as if we typically need at least to double the known amounts of reasonably active mass in the disks of Sc galaxies – beyond the gas amounts that they are known to possess – in order that such galaxies appear about as few-armed as they often are. And from where can they have obtained ... such relatively cool additional disk material if not from recent infall " (emphasis added). So another limitation of the Sparke & Sellwood model – and of other n-body simulations – is the lack of continued cosmological infall of cold gas (Combes 2008a; Bournaud & Combes 2002).
Lacking gas, the bar cannot commit suicide by transporting gas to the center and building a pseudobulge that makes it more difficult for x1 orbits to precess together. I believe that n-body studies overestimate the robustness of bars when they give them no opportunity to increase the central mass concentration.
Concurrently, the bar cannot continue to grow stronger if the model does not include a "live halo" of particles that can act as an angular momentum sink.
These comments are not meant to be critical of Sparke & Sellwood (1987). Sellwood & Carlberg (1984) recognize the importance of gas infall to the maintenance of spiral structure. Sparke & Sellwood (1987) is a clean study with the machinery that was available at the time. It focuses on fundamentals that we need to understand. Many n-body studies both before and since have led to similar conclusion and have further extended our understanding of bar evolution (e. g., Athanassoula 2003, 2005, 2012).
My remarks are meant to highlight how much this subject presents opportunities to students now. There is a danger that we may miss important physics because we do not yet observe the early stages of bar formation. This is an opportunity for observers of high-z galaxies. Modulo this uncertainty:
I suggest that bars grow secularly via an ongoing competition between outward angular momentum transport that strengthens the bar and the buildup of pseudobulges that weaken the bar. This competition allows some barred galaxies to have both strong bars and high-mass (pseudo)bulges that create (otherwise destructive) ILRs near the center.
Both the disk and the dark halo are angular momentum sinks. For the halo, this conclusion is based mostly on n-body simulations (e. g., Sellwood 1980, 2006, 2008; Athanassoula 2003, 2005; Athanassoula & Misiriotis 2002), but note that Valenzuela & Klypin (2003) conclude that the effect is often overestimated. For the disk, global spiral structure is the visible sign that the process is ongoing.
Cold gas is important to the evolution for many reasons. It makes the disk more responsive, both via its small velocity dispersion and by making new stars that keep the disk cold. Radial redistribution of gas is one product of angular momentum transport. And especially important is the conclusion reviewed in the next sections that gas driven inward to the center builds substantial pseudobulges in many galaxies. The natural frequencies at which ILR orbits want to precess therefore become less constant with radius. When this effect wins the above competition, the bar is weakened or destroyed. Continued cosmological infall of cold gas is central to all of these processes.
I argue in the rest of this review that many aspects of the above story are well understood but that many opportunities remain to be explored.
4.3.3. Vertical buckling of bars and the formation of box-shaped bulges
The vertical thickening of bars into "box-shaped bulges" is reviewed from a theoretical perspective in SW93 and from an observational perspective in Kormendy & Kennicutt (2004). My review here is brief.
N-body simulations show that strong bars thicken in the axial direction until they look peanut-shaped when viewed side-on and box-shaped when viewed at the most common orientations between side-on and end-on. The first paper to show this – Combes & Sanders (1981) – was one of the earliest papers on galaxy secular evolution. Two distinct processes are responsible.
Figure 15 shows the evolution of an n-body bar that, seen side-on, turns into a "box-shaped bulge" via a buckling instability in the axial direction (Raha et al. 1991). The instability happens after the bar is well formed, and its growth is about as rapid as that of the original bar instability. Two bar rotations later, the bar has weakend considerably, grown more centrally concentrated, and become box- or peanut-shaped as seen side-on. The resemblance to box-shaped bulges in edge-on galaxies (Section 5.2.9), already noted by Combes & Sanders (1981) is compelling. Many other n-body studies reach similar results (e. g., Athanassoula & Misiriotis 2002; Athanassoula 2003, 2005; Athanassoula et al. 2005; Shen et al. 2010).
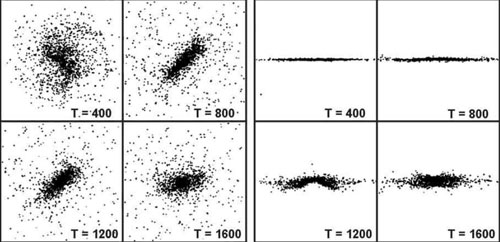 |
Figure 15. Face-on (left) and edge-on (right) views of the vertical buckling of an n-body bar and the formation of a "box-shaped bulge" (Figs. 1 and 2 from Raha et al. 1991). The rotation period at the end of the bar is ΔT ≃ 200 time units. |
A second mechanism by which bars may thicken in the axial direction is via resonances between the rotation of the bar and the vertical oscillations of disk stars (e. g., Pfenniger 1984, 1985; Combes et al. 1990; Pfenniger & Norman 1990, 1991; Pfenniger & Friedli 1991; Hasan et al. 1993). When the vertical oscillation of stars is in resonance with the azimuthal rotation of a bar, each star repeatedly encounters the bar at a similar phase in its orbit. This pumps up the vertical velocity dispersion of disk stars and gives the center a boxy appearance when viewed edge-on. Unlike bar buckling, resonant heating is inherently a secular process.
The relative importance of these two processes in making the observed "box-shaped bulges" is not known. However, the most important conclusion appears robust regardless of the answer: when we see a boxy bulge in an edge-on galaxy, it is part of the bar and not a merger remnant. We therefore call these features "box-shaped pseudobulges". I return to them in Section 5, when I discuss the evolution that bars drive in their galaxies.
4.3.4. Bar suicide and the origin of lens components. I. N-body simulations
Early n-body simulations suggested that bars are very robust (see SW93). The reason is now clear: those simulations contained no gas and so could not engineer big changes in the central concentration of the mass distribution. More recent simulations which allow the galaxy to grow a central mass – either "by fiat" or more naturally by rearranging the disk gas – show that bars tend to commit suicide by the secular evolution that they drive. In particular, they force disk gas to fall toward the center, where it builds up a high-central-concentration pseudobulge, and this causes the bar to weaken. Pseudobulge growth is covered in later sections. The death of bars and their evolution – I suggest – into lens components is discussed here.
The earliest simulations of this process were motivated by the observation that most galaxies contain central supermassive black holes (Kormendy & Richstone 1995). The earliest paper that I know, Norman & Hasan (1990), already got essentially the modern answer: "It is estimated that a black hole with mass equal to 17 % the total mass is required to destroy the [x1] family of orbits and hence the bar." No galaxy is known to have such a big black hole (Kormendy & Ho 2013), but we now know that a centrally concentrated pseudobulge – although less effective than a point mass – has a similar effect. Hasan & Norman (1990) is a detailed followup. Pfenniger & Norman (1990) concentrated on pseudobulge building by a combination of inward radial gas flow and resonant vertical heating, and they reached similar conclusions about bars destruction. Subsequent discussion has centered on the question of how much central mass is needed to affect a particular degree of bar weakening. Apparent disagreements between papers mainly result from the fact that fluffier central mass concentrations are less damaging to bars.
Why central mass concentrations are destructive is easy to see using Fig. 11 and was summarized in Section 4.2. As the central mass increases, the central maximum in Ω - κ/2 becomes higher and broader in radius (see the panel for M 81). This shrinks the radius range in which Ω - κ/2 varies slowly with radius and in which it is possible to have Ωp ~ Ω - κ/2. To put it differently, the radius range between ILR and corotation in which x1 orbits align with the bar gets smaller. Recall that x2 orbits interior to ILR align perpendicular to the bar. So, as the central concentration increases, there are fewer bar-supporting x1 orbits, and they have a harder time all precessing at the same rate Ωp ~ Ω - κ/2. As the bar potential weakens, self-gravity becomes less able to keep all the orbits precessing together. Once an orbit "escapes" from its alignment with the bar, it phase-mixes azimuthally in a short time. Even if there is no big change in orbital eccentricities, the long, thin shelf in surface brightness that makes up the bar will, I suggest (Kormendy 1979b), tend to phase-mix azimuthally into a lower-surface-brightness and more axially symmetric shelf in surface brightness that has the same sharp outer edge that the bar had. This is precisely a description of a lens component. It is part of the reason why I suggest that, as strong bars weaken, the stars that escape from them grow a lens. I suggest further that we see galaxies at all phases of this evolution: some have bars and no lenses; many have bars embedded in lenses of the same major-axis size, and some have lenses with no bars.
The rest of this section reviews further papers on bar suicide and observational evidence that lenses are defunct bars.
Combes (2008b, 2010, 2011) gives brief theoretical reviews of bar-to-lens evolution. She also reviews an additional important aspect of bar dissolution. When gas loses angular momentum and flows toward the center, the stellar bar receives that angular momentum that is lost by the gas. This makes the orbits rounder and the bar weaker. Papers that emphasize this effect include Bournaud & Combes (2002) and Bournaud et al. (2005).
My lectures included an example from Norman et al. (1996) of an n-body simulation of the weakening of a bar by a growing central mass. This is illustrated in Fig. 16. A Kuz'min – Toomre disk that contains 75% of the mass is the only component modeled with (50,000) "live" particles. The rest of the mass is in a rigid bulge. This is modeled as the sum of two Plummer spheres, initially of the same size; the aim was to let one of them shrink in radius once the bar was well established. The disk was initially given a Toomre stability parameter of Q = 1 ensuring that a bar would form. This already guarantees that the initial bar will coexist with a bulge whose B / T ratio is typical of observed galaxies. Figure 16 shows that the inner part of the disk formed a bar by time 50; if nothing further was done to the model (top row of particle distributions and "no central mass" amplitude line in the middle panel), the bar remained stable in amplitude to time 200.
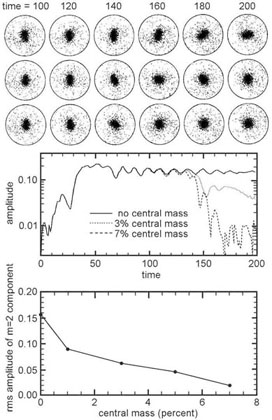 |
Figure 16. Death of an n-body bar as the central mass concentration is increased (adapted from Figs. 1, 2 and 3 of Norman et al. 1996). An initial axisymmetric disk was evolved to time 100, by which time a stable bar had developed (leftmost configuration shown in each of the three rows of particle distributions at the top). The top three rows show the time evolution as a point mass is grown at the center. Its mass shrinks from bulge size to zero size between t = 100 to t = 150. At the end, it makes up 0%, 3% and 7% of the mass of the disk (top row to bottom row). In the absence of a central point mass, the bar is stable (top). The bar is weakened progressively more as the central mass increases. The bar amplitude is shown in the middle panel. The bottom panel shows the t = 200 amplitude as a function of the final central point pass. Note that, whereas higher point masses more thoroughly destroy the bar, its amplitude is non-zero even for a 7% central point mass. |
Between time 100 and time 150 (about four bar tumbling periods), the lower-mass "bulge" Plummer sphere was shrunk by a factor of 50 in radius. Note that this turns it effectively into a point mass, not a pseudobulge with a realistic scale length. No mass was added, so the overall equilibrium of the disk was essentially unaffected. But the amplitude of the bar decreased as the central point mass was shrunk. Even a 3% central point mass reduced the bar amplitude substantially. A 7% point mass killed it almost completely.
Norman et al. (1996) explored the mechanism whereby the bar is destroyed in some detail, both in the above, two-dimensional simulation and in three-dimensional simulations that give similar results. In essence, moving some mass to the center shrinks the phase space (e. g., radial range) of the x1 orbits. As ILR moves outward, some x2 orbits appear, and these do not support the bar. Some orbits become chaotic. At some point (time ~ 140 ± 5 in Fig. 16), the bar coherence quickly breaks down and the disk becomes more axisymmetric. Note that the bar is not destroyed completely.
Norman and collaborators acknowledge that these are "highly idealized calculations intended to study just one aspect of the rich secular evolution of barred galaxies. The contraction of a rigid mass component is, of course, highly artificial," and more to the point, the pseudobulges that weaken real bars have length scales ~ 1/10 those of their associated disks; they are not point masses. With Norman et al. (1996), we emphasize that the model is constructed so a relatively large bulge coexists comfortably with the bar. Figure 16 should be taken as a "proof of concept" of bar suicide, not as a definitive measurement of how much central mass concentration is required to achieve it. I use Norman et al. (1996) and not more detailed simulations as my example here because my purpose is primarily pedagogical, and I don't want the essential theme to get lost in the details of orbit analysis.
The real world is substantially more complicated in ways that make it difficult to predict via simulations how much central mass concentration a bar can tolerate. No available simulation realistically follows the competition between (1) the bar growth that results from allowing the disk and dark halo to be angular momentum sinks, with the disk kept cold and continually replenished with cosmologically infalling gas, and (2) the secular evolution that builds up the central mass concentration and that thereby fights the growth of the bar. While the pseudobulge grows both through gas infall and star formation and (e. g., Norman et al. 1996) by the redistribution of stars, resonances such as (but not limited to) ILR sweep through the central regions and continually keep a fresh supply of material responsive to resonant interactions with the bar.
So it is no surprise that some papers suggest that central mass concentrations as small as a few percent of the disk mass are enough to destroy bars (e. g., Berentzen et al. 1998; Sellwood & Moore 1999; Hozumi & Hernquist 1999, 2005; Bournaud et al. 2002, 2005; Hozumi 2012) whereas others (e. g., Friedli & Benz 1993; Norman et al. 1996; Athanassoula et al. 2005) find that larger masses are necessary. These apparent disagreements are largely resolved by a fundamental conclusion due to Shen & Sellwood (2004): "For a given [central] mass, dense objects cause the greatest reduction in bar amplitude, while significantly more diffuse objects have a lesser effect" (emphasis added). The culprit in bar suicide is certainly not the central supermassive black hole (Shen & Sellwood 2004) or even a nuclear star cluster, since these typically have masses of ~ 0.2% of the mass of a classical bulge and a smaller fraction of the mass of a pseudobulge or disk (see Kormendy & Ho 2013 for a review).
The results of Shen & Sellwood (2004) suggest that pseudobulges mainly are responsible for destroying bars. For a "soft" central mass whose size is comparable to that of a pseudobulge, Shen and Sellwood find that a 5% central mass decreases the bar strength to ~ 60% of its undamaged value, whereas a 10% mass decreases the bar strength to ~ 1/3 of its undamaged value. Orbital analysis reveals that the bar dies because the phase space of x1 orbits shrinks, and many x1 orbits become chaotic as the bar decays. In most of these models, the dark matter halo was a rigid potential and therefore not an angular momentum sink. Test runs with a live halo show that the bar is then slightly harder to destroy. Similarly, the disk is dissipationless and does not accrete cold gas from the cosmological web, so it is not as good an angular momentum sink as the disk in a real spiral galaxy. Nevertheless, these results provide a realistic picture of what it takes to destroy a bar, at least as judged by a comparison with real galaxies (Section 4.3.5).
4.3.5. Bar suicide and the origin of lens components. II. Observations
Long before we knew of a process that could destroy bars, Kormendy (1979b, 1981, 1982b) suggested that bars weaken with time and evolve into lenses. Observations on which this suggestion was based include the following.
Lens components are very common in barred galaxies; in the sample of 121 SB galaxies studied by Kormendy (1979b), 54% of SB0- to SBa galaxies have lenses. The relative light contribution of the bar and lens varies widely from bar / lens ≫ 1 to bar / lens ≪ 1. Figure 17 shows such a sequence. I illustrate many B(lens) structures in these lectures to emphasize how common they are.
 |
Figure 17. Typical galaxies in which a bar fills a lens component in one dimension. This figure shows a sequence from a strong bar with essentially no lens (NGC 4643) through galaxies that have both bars and lenses (NGC 2950, NGC 4340, NGC 3945) to NGC 3081, which has an exceedingly weak bar embedded in a bright lens with a very bright, star-forming inner ring around the rim of the lens. The HST image at right is an enlargement of the inner ring, lens, bar and pseudobulge. In NGC 3081, the pseudobulge replicates the main B(r,lens) structure with a nuclear bar. All images are from http://www.wikisky.org except those of NGC 3081, which are from the de Vaucouleurs Atlas of Galaxies (Buta et al. 2007: left image) and HST (Buta et al. 2004: right image). Similar galaxies are shown in earlier figures. In Fig. 6, NGC 1291 is an (R)SB(lens)0/a galaxy similar to NGC 3945 here. In Fig. 9, NGC 2859 is an (R)SB(lens)0 galaxy similar to NGC 3945. The other galaxies in that figure are later-Hubble-type versions of the sequence shown here. |
Lens components occur but are rare in unbarred S0 – Sa galaxies. Examples are shown in Figs. 7 and 18. It is likely that the inner "oval disks" in later-type (typically Sb) galaxies are lenses, too. If B → lens evolution occurs, this suggests that it goes nearly to completion (i. e., bar / total light → 0) rarely in early-type galaxies and more commonly in mid-Hubble-type galaxies.
 |
Figure 18. The prototypical unbarred S0 galaxy with a lens is NGC 1553 (Fig. 7). This figure shows two more examples. NGC 2784 is from the de Vaucouleurs Atlas and NGC 3245 (rotated so north is at left) is from http://www.wikisky.org. The lenses are the elliptical shelves in surface brightness just outside the (pseudo)bulges. Several earlier figures show barless, late-type analogs which probably also are lenses (NGC 4736 in Figs. 3, 6 and 8; NGC 4151 in Fig. 8). |
Lens components and bars in early-type galaxies have similar radial brightness profiles; i. e., shallow surface brightness gradients interior to a sharp outer edge. The brightness profiles of the lenses measured in Kormendy & Bender (2012) are well fitted by Sérsic (1968) functions with n ≃ 0.5 (i. e., Gaussians).
When bars and lenses occur together, the bar almost always fills the lens in one dimension (Kormendy 1979b, Buta et al. 2007; Buta 2011, 2012; Fig. 17 and references there). Points (c) and (d) imply that, to make a lens, it is sufficient to azimuthally phase-mix bar orbits. Points (a) and (b) hint that such a process occurs in many barred galaxies but that bars are completely destroyed only rarely. This is consistent with Section 4.3.4: moderate "soft" mass concentrations weaken bars but do not necessarily destroy them.
Figure 19 shows a compelling observation that supports B → lens evolution. The top panels show rotation velocity V and velocity dispersion σ along the major axes of the barred S0(lens) galaxy NGC 3945 (Fig. 17) and the unbarred S0(lens) galaxy NGC 1553 (Fig. 7). The NGC 3945 bar is oriented along the minor axis, so the major-axis observations in Fig. 19 really measure the lens. The bottom panel shows V / σ for these two galaxies plus NGC 2784 (Fig. 18) and two more SB0 galaxies. I conclude: (1) The inner part of each lens is hotter than its corresponding pseudobulge. That is, σ is higher and V is smaller in the lens than in the pseudobulge. (2) This behavior and the V / σ radial profiles are the same in barred and unbarred lenses. (3) And V / σ in these lenses is similar to V / σ along the ridge line of the strong bar in NGC 936 (Kormendy 1983).
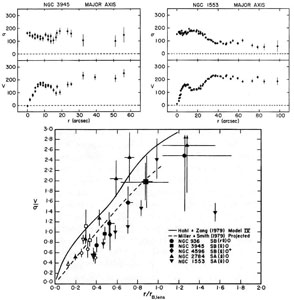 |
Figure 19. (top) Major-axis rotation velocity V and velocity dispersion σ data in NGC 3945 [SB(lens)0] and in NGG 1553 [SA(lens)0]. The lens radius is 51" in NGC 3945 and 36" in NGC 1553. The instrumental dispersion is ~ 100 km s-1 for NGC 3945 and ~ 65 km s-1 for NGC 1553. (bottom) Local ratio of rotation velocity to azimuthal velocity dispersion in lenses of barred and unbarred galaxies. Radii are normalized to the radius of the lens for galaxies and to the corotation radius for the n-body models. Horizontal "error bars" show the range in radii over which data were averaged. Open symbols refer to measurements contaminated by bulge light. This figure is taken from Kormendy (1981, 1982b, 1984a). |
Thus the relative importance of ordered motions (rotation) and random motions is similar in lenses and bars, both observed and n-body-simulated. In particular, at about 40 % of the radius rlens of the lens, V / σ ~ 0.8. Also, σ is the line-of-sight velocity dispersion, so the total velocity dispersion is likely to be at least a factor of √2 larger. This means that the ratio of rotational kinetic energy to random kinetic energy is ~ 1/3 in the inner parts of both bars and lenses. That is, stellar orbits are similarly far from circular. Lenses are parts of disks (Freeman 1975), and yet they are hotter than their associated (pseudo)bulges. The close similarity of V2 / σ2 in bars and lenses (cf. Bosma et al. 2010) means that it is relatively easy for bars to evolve into lenses – it is enough if x1 orbits escape the persuasion to precess together that is supplied by bar self-gravity; it is not necessary to change their energies and angular momenta drastically.
The fact that we see arbitrarily weak bars embedded in strong lenses is a powerful argument that these bars were once stronger (Kormendy 2004b). NGC 3081 in Fig. 17 is the best example. It contains an exceedingly faint bar, but almost all of the inner light is in the lens – which is much rounder – and the pseudobulge. Can we really imagine that one or two percent of the stars in a disk discover that they are bar-unstable, that they make a nice, highly elongated bar, and that most of the disk meanwhile stays just slightly oval? This is not what happens in n-body simulations of bar formation. There, essentially all of the disk participates in the instability, and most disk stars that live interior to the final radius of the bar participate in the bar. That's why n-body bars buckle in the axial direction – they are self-gravitating structures. Lenses, on the other hand, appear to be flat (e. g., Kormendy 1982b and Kormendy & Bender 2012). Thus the observation (Figs. 17 and 18) that there is a complete continuity from bar / lens ≫ 1 to bar / lens ≪ 1 to bar / lens = 0, together with the above results, strongly suggests that bars evolve into lenses. The fact that barless lenses are rare at early Hubble types implies that any evolution is relatively slow or that it stops when a galaxy gets transformed into an S0. The observation of barless ovals that appear to be equivalent to lenses in galaxies such as NGC 4736 and NGC 1068 implies that the evolution goes to completion more readily in galaxies that contain gas.
All of these suggestions are comfortably consistent with – and arguably could have been predicted from – our picture that bars drive secular evolution that builds up the central density by forming pseudobulges that are harmful to the survival of the bar.
I do not want to argue too forcefully for this picture. I especially do not want to suggest that bar → lens evolution is the only thing that happens. But the most economical suggestion that is consistent with observations and simulations is that bars evolve away as they increase the central concentration of the galaxy. One result is lens components that have the same radii, shallow brightness gradients, and sharp outer edges as their parent bars. Some tests of this idea are suggested in Section 4.3.7.
We get a preliminary idea of what PB / T ratio divides SA and SB galaxies by examining values for intermediate-Hubble-type oval galaxies that are illustrated in this paper. Two more such galaxies are shown in Fig. 20. Table 1 shows the results. The sample is small. Also, PB / T ratios of SAB galaxies vary widely, perhaps because the central concentrations of pseudobulges vary widely. Nevertheless, we derive a clean result, as follows.
 |
Figure 20. Oval galaxies that bracket the PB/T value which divides galaxies that do and do not have bars. The barred galaxy NGC 3393 has PB / T = 0.27 ± 0.06; the unbarred galaxy UGC 3789 has PB / T = 0.32 ± 0.03. This figure from Kormendy & Ho (2013) is based on Digital Sky Survey images from http://www.wikisky.org. |
Table 1 suggests that realistic pseudobulges with PB / T ≃ 0.34 ± 0.02 are massive enough to destroy bars essentially completely and to convert them into lenses. This is a preliminary result, reported here for the first time.
| Galaxy | Type | PB / T | Source |
| NGC 2273 | (R')SBa | 0.19 ± 0.02 | Kormendy & Bender (2013) |
| NGC 3393 | (R')SBab | 0.27 ± 0.06 | Kormendy & Bender (2013) |
| NGC 3081 | (R')SAB0/a | 0.11± 0.000 | Laurikainen et al. (2010) |
| NGC 3368 | (R')SABab | 0.25± 0.000 | Kormendy & Bender (2013) |
| NGC 4151 | (R')SABab | 00.327± 0.000 | Gadotti (2008) |
| UGC 3789 | (R)SAab | 0.32 ± 0.03 | Kormendy & Bender (2013) |
| NGC 1068 | (R)SAb | 0.35 ± 0.05 | Kormendy & Bender (2013) |
| NGC 4736 | (R)SAab | 0.36 ± 0.01 | Kormendy & Bender (2013) |
4.3.7. Remaining puzzles and suggestions for further work
Our understanding of the lives and deaths of bars is now reasonably well developed. A few particularly obvious problems and suggestions about how to address them are outlined below.
How do bars form? Despite the long history of seeing violent instabilities when n-body systems are given small Toomre Q by fiat, and despite convincing hints that tidal tickling helps, we understand bar formation less well than we think. We need to investigate bar growth both observationally by observing distant galaxies and by using simulations. Closely related and very important are (b) and (c).
We need to study bar evolution via the competition between angular momentum sinks (the outer disk and dark halo), which make the bar grow stronger, and the increasing importance of ILR as the bar moves material inward, which makes the bar grow weaker. This is a complicated modeling job. But the great richness of possible interactions between nonaxisymmetric components is lost when the relevant components either are not included or are turned into fixed potentials. I do not criticize published papers for trying to distill clean subsets of the physics that we want to study. But there are effects that we cannot find if component interactions are switched off. In particular, it is likely that a bar can coexist with a more massive (pseudo)bulge if it grew in the context of the above competition.
Including gas is critically important in studying bar evolution. Gas dissipation is essential for the inward flow of the material that builds pseudobulges. Whether recycled, not yet used up, or accreted from outside, gas helps to keep the disk cold enough to be responsive. Without it, n-body disks get so hot that spiral structure switches off and the disk gets less effective at absorbing angular momentum. Cosmological accretion of cold gas may be essential for realistic bar evolution.
On the observational front, we need to measure the luminosity and mass functions of elliptical galaxies, classical bulges, pseudobulges and disks as a function of environmental density. Early observations demonstrate that the answers are different in clusters and in the field (Sandage et al. 1985a; Kormendy et al. 2010). But we need more quantitative measures of the relative importance of secular evolution and hierarchical clustering and merging as a function of environment.
The idea that bars evolve into lenses needs to be tested further. Note how many relevant observations and theoretical hypotheses date from the 1980s. This is an opportunity for today's students. We need absorption-line kinematic measurements of bars and lenses. We need photometry and component decomposition to see, e. g., whether the bar/lens luminosity ratio tends to be smaller as the (pseudo)bulge is more massive or more centrally concentrated. Caution: many decomposition codes use the assumption that each component has a flattening that is independent of radius. This is certainly wrong and commonly leads to unphysical conclusions (e. g., about numbers of components). And we need mass models to determine halo properties. There is much work to be done.