2. EVOLUTION OF THE PRIMORDIAL GAS IN THE FORMATION OF THE FIRST GALAXIES

Being composed solely of the hydrogen, helium, and trace amounts of lithium and beryllium synthesized in the Big Bang, the primordial gas contains a limited number of coolants, chief among these H₂ at temperatures ≤ 10⁴ K. Because of the ineffecient cooling of the gas relative to the metal-enriched ³ gas from which stars form today, it is likely that the Pop III initial mass function (IMF) is top-heavy compared to that of the stars observed in our Milky Way. A simple explanation for this is based on the mass scale at which the fragmentation of the primordial gas takes place. Known as the Jeans mass M_J, this is essentially the mass at which density enhancements grow via gravity more quickly than they can be erased due to pressure gradients. To estimate M_J for a gas with a number density n and a temperature T, related to the sound speed c_s by 3k_B T / 2 = µ m_h c_s² / 2, we first estimate the timescale at which density enhancements grow as the free-fall time t_ff ≃ (G ρ)^−1/2 = (G µ m_h n)^−1/2, where G is Newton's constant. Then, estimating the timescale in which density enhancements are erased as the sound-crossing time t_sc ≃ L / c_s, we equate these two timescales to estimate the characteristic size L_J and mass of a gas cloud which is just massive enough to collapse under its own gravity. We thus arrive at an expression for the Jeans mass M_J, given by

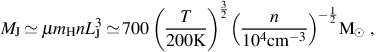(4)

where we have assumed µ = 1.2, appropriate for neutral primordial gas, and have again normalized to quantities typical for primordial star-forming clouds. As we shall discuss in Section 3, the primordial gas is in general unable to cool as efficiently as metal-enriched gas, which leads in general to higher temperatures at fragmentation and so to a larger characteristic mass of the gravitationally unstable gas clouds from which stars form (e.g. Bromm & Larson 2004).

While the Jeans mass is an estimate of the mass of a collapsing gas cloud, the amount of gas that is finally incorporated into a star is also dictated by the rate at which gas accretes onto it, starting from the formation of a protostar. Thus, another reason that primordial stars are likely to be more massive than stars forming from metal-enriched gas is that higher gas temperatures also translate into higher accretion rates, as can be seen by estimating the accretion rate _acc as a function of the temperature of the gas (see e.g. Stahler et al. 1980). Assuming that, through the action of gravity, the protostar grows by accreting from a gas cloud of mass ≃ M_J, the accretion rate can be estimated as accretion

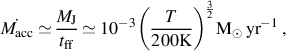(5)

where we have again assumed µ = 1.2 and normalized to the characteristic temperature of the gas from which Pop III stars form in minihalos (see e.g. Glover 2005). Therefore, it is a combination of both the relatively large reservoir of gas available in gravitationally unstable gas clouds and the relatively high accretion rates onto primordial protostars (e.g. Omukai & Palla 2003; Tan & McKee 2004; Yoshida et al. 2008) which suggests that Pop III stars are more massive than metal-enriched Pop II or Pop I stars. As both M_J and _acc depend strongly on the temperature of the gas, one of the central questions with regard to star formation in the first galaxies is the degree to which the gas is able to cool. In the next Section, we discuss the cooling of primordial gas in the first galaxies, focusing on how it is different from the case of cooling in the minihalos in which the first stars form. Later, in Section 3.3, we discuss how the cooling properties of the primordial gas change when it is mixed with heavy elements and collapses to form the first Pop II stars.

2.1. Cooling of the Primordial Gas

As shown in Figures 2 and 3, the primordial gas collapsing into atomic cooling halos is typically shock-heated to the virial temperature of ≥ 10⁴ K. In contrast to the case of Pop III star formation in minihalos, the gas at these temperatures is partially ionized, and this can have important consequences for the evolution of the gas as it collapses to form stars in the first galaxies. To see why, we note that the primary reaction sequence leading to the formation of H₂ molecules is (e.g. Galli & Palla 1998; Glover 2005) H₂

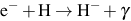(6)

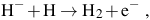(7)

where γ denotes the emission of a photon. Whereas the primordial gas which collapses into minihalos to form the first stars has a free electron fraction X_e ≤ 10⁻⁴, the collisional ionization of the primordial gas collapsing into atomic cooling halos can lead to an enhancement of the free electron fraction by a factor of more than an order of magnitude, as shown in Figure 3. In turn, this leads to high rates of H₂ formation in atomic cooling halos, principally via the above reactions for which free electrons act as catalysts (e.g. Shapiro & Kang 1987). The net result is a generally higher H₂ fraction in the high density, central regions of atomic cooling halos than in minihalos, as is also shown in Figure 3, and hence also to higher cooling rates due to molecular emission. Therefore, somewhat counter-intuitively, because of the higher virial temperatures of the atomic cooling halos in which the first galaxies form, the dense gas in the centers of these halos can cool more effectively than in the minihalos in which the first Pop III stars form.

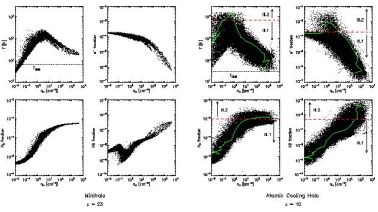Figure 3. The properties of the primordial gas inside a first star-forming minihalo at z = 23 (left panel) and a first galaxy-hosting halo at z = 10 (right panel), as found in a cosmological hydrodynamics simulation. The temperature, electron fraction, HD fraction, and H2 fraction are shown as functions of number density, clockwise from top left to bottom left. Left panel: In the minihalo case, adiabatic collapse drives the temperature to T ≥ 103 K and the density to n ≥1 cm3, where molecule formation sets in and allows the gas to cool to ≃ 200 K. At this point, the central clump becomes Jeans-unstable and presumably collapses to form at least one massive Pop III star. Right panel: In the first galaxy, formed in an atomic cooling halo, a second cooling channel emerges due to an elevated electron fraction at the virial shock, where the temperature rises to ∼ 104 K; this, in turn, enhances molecule formation and allows the gas to cool to the much lower temperatures, as shown by the evolutionary track of a representative parcel of gas (green lines). Due to the correspondingly lower Jeans mass (equation 4) and accretion rate (equation 5), less massive Pop III stars (Pop III.2; see Section 2.1) are expected to form in such a first galaxy, perhaps with a characterisitic mass of the order of ≃ 10 M⊙. From Greif et al. (2008).

In fact, the ionization of the primordial gas in atomic cooling halos results in the formation of another molecule which can be even more effective at cooling the gas than H₂: deutrerium hydride (HD). With the high H₂ fraction that develops in partially ionized gas, HD forms rapidly via the following reaction:

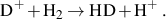(8)

While deuterium is less abundant in the primordial gas than hydrogen by a factor of the order of 10⁻⁵, the HD molecule is able to cool to temperatures considerably lower than H₂ (e.g. Flower et al. 2000). Firstly, this owes to the fact that HD has a permanent dipole moment, allowing dipole rotational transitions, which spontaneously occur much more often than the quadrupole rotational transitions in H₂. Also, the dipole moment of HD allows transitions between rotational states of Δ J = ± 1, which are of lower energy than the Δ J = ± 2 quadrupole transitions of H₂. Thus, collisions with other particles, such as neutral hydrogen, can excite the HD molecule from the ground to the first excited rotational state (J = 1), from which it decays back to the ground state by a dipole transition. The photon that is emitted in the process carries away energy and thus cools the gas. Because HD can be excited to the J = 1 state by relatively low energy collisions, and because its subsequent radiative decay occurs quickly compared to that of H₂, the cooling rate per molecule is higher for HD than H₂ at temperatures ≤ 100 K, as shown in Figure 4.

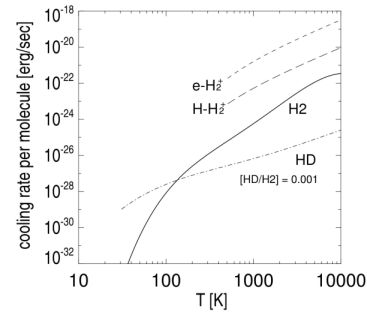Figure 4. Molecular cooling rates for H2 (solid line), HD (dot-dashed line), and H2+ (dashed lines). Owing primarily to the permanent dipole moment of HD, at low temperatures the cooling rate per HD molecule is significantly higher than that per H2 molecule. Thus, primordial gas enriched in HD is able to cool to much lower temperatures than gas containing solely H2; indeed, as is shown in Section 2.1, primordial gas sufficiently enriched in HD can cool to the lowest temperature attainable by radiative cooling, that of the CMB. While the cooling rates per H2+ molecule (shown here for collisional excitation by free electrons and hydrogen atoms) can be very high, the low abundance of this molecule limits its importance for the thermal evolution of the primordial gas. Finally, we note that at temperatures ∼ 104 K, the primordial gas is cooled primarily by recombination and resonance lines of atomic hydrogen (not shown). From Yoshida et al. (2007a).

Whereas in cosmological minihalos H₂ cooling alone can cool the gas to ≃ 200 K, as shown in the left panel of Figure 3, HD cooling can be so effective as to allow the primordial gas to cool to the lowest temperature that can be achieved via radiative cooling, that of the cosmic microwave background (CMB), T_CMB = 2.7(1 + z) (e.g. Larson 2005; Johnson & Bromm 2006; Schneider & Omukai 2010). It is useful at this point to derive this fundamental result, as we will draw on the formalism introduced here later as well, in discussing the impact of the first heavy elements on the cooling of the primordial gas (see Section 3.3).

To begin, note that the frequency ν₁₀ of emitted radiation for the rotational transition J = 1 → 0 of HD can be expressed as

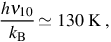(9)

where k_B is the Boltzmann constant and h is the Planck constant. For clarity, here we shall consider the simple case in which only this transition and its reverse occur. Next, consider a finite parcel of primordial gas with a temperature T_gas. For simplicity, we shall assume that the density of the gas is sufficiently high to establish local thermodynamic equilibrium (LTE) level populations according to the Boltzmann distribution ⁴

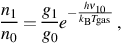(10)

where n_i is the number density of HD molecules in the ith excited rotational state and g_i is the statistical weight of that state; specifically, here we have g₁ = 3 g₀. Furthermore, as we are considering only transitions between the ground state and the first excited state, we shall take it that no other rotational levels are occupied. Equivalently, we take it here that T_gas < 130 K, as otherwise collisions with other particles would be sufficiently energetic to excite the molecule to higher levels. Finally, we make the assumption that T_gas ≥ T_CMB. Thus, if we denote the specific intensity of the CMB, which is an almost perfect blackbody, at the frequency ν₁₀ as I_ν10, then it follows that

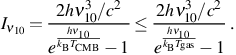(11)

Now, with the Einstein coefficients for spontaneous and stimulated emission from J = 1 → 0 denoted by A₁₀ and B₁₀, respectively, and that for absorption of a photon effecting the transition J = 0 → 1 by B₀₁, we have the standard relations B₁₀ g₁ = B₀₁ g₀ and

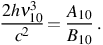(12)

Along with equations (10) and (11), these imply that

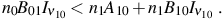(13)

Thus, the gas is cooled, as more energy is emitted into the CMB radiation field than is absorbed from it. The rate at which the temperature drops can be found by first expressing the energy density of the gas as

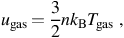(14)

where n is the total number density of the gas particles, including all species. With this, equation (13) implies that, with no change in the density of the gas,

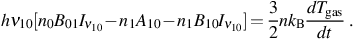(15)

Next, we take it that the ratio of the number density of HD molecules n_HD to the total number density of particles n in the gas is given by the constant factor

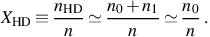(16)

Then using equations (10), (11), and (12) in equation (15), and neglecting stimulated emission for simplicity, the thermal evolution of the gas is approximately described by

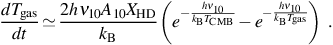(17)

It is clear from this result that if T_CMB ≤ T_gas < 130 K, with the gas cooling only by radiative decay of the excited rotational state J = 1 to J = 0, the temperature of the gas will asymptotically approach T_CMB. Thus, equation (17) describes the fact that the CMB temperature is indeed a lower limit on the temperature to which a gas can cool via line emission only. Using the previous equation, we can estimate the timescale for reaching the CMB temperature floor as

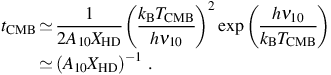(18)

Finally, we may use this timescale to define a critical HD abundance above which the gas may cool to the CMB, by demanding that the gas is able to cool faster than it is heated by compression during its collapse, which takes place roughly on the free-fall timescale. We thus require that t_CMB∼ t_ff, where the free-fall time is calculated at the characteristic density n ∼ 10⁴ cm⁻³ at which the primordial gas is found to fragment in cosmological simulations (e.g. Bromm & Larson 2004). With A₁₀≃ 5× 10⁻⁸ s⁻¹ for this transition (e.g. Nakamura & Umemura 2002), we thus find the critical HD abundance to be approximately

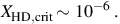(19)

If the abundance of HD is lower than X_{HD, crit}, the gas will not have time to cool to T_gas ≃ T_CMB during its collapse. As shown in Figure 3, for the case of the primordial gas cooling in the first galaxies a large fraction of the gas at densities n ≥ 10 cm⁻³ has an HD abundance greater than X_HD,crit, whereas in the case of cooling in the minihalos hosting the first stars the HD fraction is in general much lower.

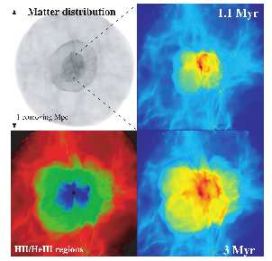Figure 5. Expansion of the H ii region around a Pop III.1 star formed in a minihalo: the large-scale density distribution at z = 26 (top left), and the projected gas density at 1.1 (top right) and 3 Myr (bottom right) after the central star turns on. The bottom left panel shows the extent of the H ii region (green) and that of the He III region (blue) at 3 Myr. When the central star turns off after this time, the strongly ionized primordial gas begins to cool and recombine, with H2 and HD molecules forming in abundance. This, in turn, enhances the cooling properties of the gas, which may later collapse and form Pop III.2 stars in a more massive halo hosting a first galaxy. From Yoshida et al. (2007a).

A high abundance of HD can, in general, be formed whenever the primordial gas becomes ionized. This occurs through collisional ionization, as in the case of shock heating to temperatures above ∼ 10⁴ K in the virialization of atomic cooling halos, but also occurs when the first stars formed in minihalos emit high energy radiation which photoionizes the gas. As shown in Figure 5, a massive Pop III star emits enough ionizing radiation to destroy almost all of the neutral hydrogen within a distance of a few physical kiloparsec ⁵ (e.g. Alvarez et al. 2006; Abel et al. 2007), via the reaction

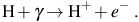(20)

Here the products are ionized hydrogen and a free electron, which has a kinetic energy equal to the energy of the ionizing photon minus the ionization potential of hydrogen, 13.6 eV. This free electron is ejected from the atom and shares it kinetic energy with other particles via collisions, thereby heating the gas to higher temperatures. Typically, an equilibrium temperature of ∼ 10⁴ K is established in H ii regions, largely set by a balance between the rate at which the gas is photoheated via the above reaction and the rate at which it is cooled by the radiative recombination and resonance emission of hydrogen (e.g. Osterbrock & Ferland 2006). While in the H ii regions around active stars the temperature is thus too high for molecules to form in large abundances due to collisional dissociation, once the central star dies the hot ionized gas begins to cool and recombine. Under these conditions, molecules form rapidly and a high abundance of HD can be achieved (e.g. Nagakura & Omukai 2005; Johnson & Bromm 2006; Yoshida et al. 2007b; McGreer & Bryan 2008).

Therefore, overall, primordial gas that has either been photoionized by a Pop III star in a minihalo or which has been partially ionized during the virialization of an atomic cooling halo, may in principle collapse and cool all the way to the temperature floor set by the CMB. This is distinct from the case of the first Pop III star formation in minihalos (e.g. Glover 2005), and this distinction motivates the following terminology (e.g. McKee & Tan 2008; Greif et al. 2008; Bromm et al. 2009) ⁶:

Pop III.1

The first generation of primordial stars formed in minihalos and not significantly affected by previous star formation.

Pop III.2

Primordial stars formed under the influence of a previous generation of stars, either by the ionizing or photodissociating radiation which they emit.

Based on the enhanced cooling of the gas due to high H₂ and HD fractions, it is expected that the typical mass scale of Pop III.2 stars is significantly lower than that of Pop III.1 stars (e.g. Uehara & Inutsuka 2000; Nakamura & Umemura 2002; Mackey et al. 2003; Machida et al. 2005; Nagakura & Omukai 2005; Johnson & Bromm 2006; Ripamonti 2007; Yoshida et al. 2007b). Following equation (4), the Jeans mass for gas that cools to the temperature of the CMB, which sets a rough upper limit for the mass of Pop III.2 stars formed from partially ionized primordial gas, is

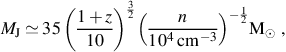(21)

where we have normalized to the same characteristic density at which the primordial gas fragments in Pop III.1 star formation (e.g. Bromm & Larson 2004). At this fixed density, the Jeans mass is roughly an order of magnitude lower than expected for the case of Pop III.1 star formation in minihalos. Also due to the lower temperature of the gas in the Pop III.2 case, the rate of accretion onto a protostar is similarly lower (Yoshida et al. 2007b):

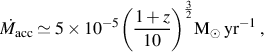(22)

compared to _acc ∼ 10⁻³ M_⊙ yr⁻¹ for the case of Pop III.1 stars (see equation 5).

While enhanced molecule abundances are likely to result in lower characteristic stellar masses, other mitigating effects also come into play in the formation of second generation primordial stars. One factor which likely becomes important for shaping the stellar IMF, particularly in atomic cooling halos (e.g. Wise & Abel 2007b; Greif et al. 2008), is the development of supersonic turbulence (see e.g. Mac Low & Klessen 2004; Clark et al. 2011b). Also, the degree to which the abundances of H₂ and HD can be raised in the first galaxies is dependent on the strength of the molecule-dissociating radiation field generated by the first generations of stars (e.g. Wolcott-Green & Haiman 2011). In the next Section, we shall see that an elevated radiation field may not only result in higher Pop III star masses, but may also result in the formation of the seeds of the first supermassive black holes.

2.2. Suppression of Cooling by the Photodissociation of Molecules

The assembly of the first galaxies becomes much more complex with the formation of the first stars, in part because they emit high energy radiation that alters the primordial gas in dramatic ways (e.g. Ciardi & Ferrara 2005). As in the case of primordial gas in the minihalos in which the first stars form, in the first galaxies one of the primary cooling processes is the emission of radiation from molecular hydrogen, and high energy radiation emitted by the first stars can easily destroy these molecules (e.g. Haiman et al. 1997; Omukai & Nishi 1999; Ciardi et al. 2000; Glover & Brand 2001; Mackacek et al. 2001; Ricotti et al. 2001). So called Lyman-Werner (LW) photons, with energies 11.2 eV ≤ hν ≤ 13.6 eV excite H₂, leading in turn to its dissociation into atomic hydrogen ⁷ (Stecher & Williams 1967):

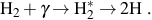(23)

With the destruction of H₂ molecules, the primordial gas cools less rapidly and this signals a change in the rate at which gas can collapse into minihalos and form Pop III stars. An estimate of the minimum LW radiation field necessary to significantly delay star formation in a minihalo can be found by comparing the timescale t_form for the formation of H₂ to the timescale for its photodissociation. For a general radiation field the photodissociation time can be expressed as t_diss ≃ 3 × 10⁴ J₂₁⁻¹ yr, where the specific intensity J_LW of the LW radiation field is defined as J_LW = J₂₁ × 10⁻²¹ erg s⁻¹ cm⁻² Hz⁻¹ sr⁻¹ (e.g. Abel et al. 1997); here, J₂₁ is a dimensionless parameter normalized to a typical level of the radiation field. To estimate the formation time we note that, as shown in the left panel of Figure 3, primordial gas collapsing into a minihalo is roughly adiabatic until its density rises to roughly n ≃ 1 cm⁻³, at which point its temperature is T ≃ 10³ K. Therefore, it is only at this characteristic density and higher that H₂ is effective at cooling the gas, in turn leading to gravitational collapse and the formation of stars. It is the formation time of H₂ in these conditions, which is t_form ≃ 10⁶ yr, that is to be compared to the photodissociation timescale t_diss. Equating these two timescales, we find a critical LW radiation field intensity of the order of J₂₁ ≃ 10⁻², at which the suppression of H₂ formation and cooling slows the process of Pop III star formation in minihalos (see Kitayama et al. 2001; Yoshida et al. 2003; Mesinger et al. 2006; Wise & Abel 2007a; Johnson et al. 2008; Trenti & Stiavelli 2009).

Figure 6 shows the results of cosmological simulations of the collapse of primordial gas into minihalos, under the influence of different levels of a constant LW radiation field. As the panels in the Figure show, for higher J_LW the primordial gas in a given minihalo collapses to form stars at lower redshift z_coll, when the halo has grown to a higher mass M_vir and has a higher virial temperature T_vir. The results of these simulations corroborate our estimate of the critical LW background, as T_vir and M_vir increase most dramatically at J₂₁ ≃ 0.04.

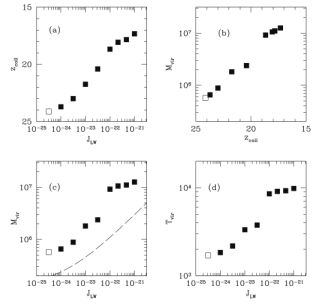Figure 6. The properties of simulated cosmological dark matter halos when the primordial gas first collapses to form Pop III stars, under the influence of various levels of the background Lyman-Werner photodissociating flux JLW (shown here in units of erg s−1 cm−2 Hz−1 sr−1): star formation redshift zcoll vs. JLW, Mh vs. zcoll, Tvir vs. JLW, and Mh vs. JLW (clockwise from top left panel). As the intensity of the background H2-dissociating flux increases, a given halo must grow to a larger mass and have a higher virial temperature before the primordial gas can cool, collapse and form stars. At a flux of JLW ≃ 4 × 10−23 erg s−1 cm−2 Hz−1 sr−1 (i.e. J21 ≃ 0.04), there is a steep increase in the Tvir and Mh of star-forming halos due to the rate of H2 photodissociation becoming comparable to the rate of H2 formation. From O'Shea & Norman (2008).

Because the mean free path of LW photons is generally large, up to ∼ 10 physical Mpc, a roughly uniform background field is quickly established when the first stars begin emitting radiation (e.g. Haiman et al. 1997). We can estimate the level of the H₂-dissociating background radiation, as a function of the cosmological average star formation rate 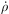_∗ per unit comoving volume, by assuming that massive stars which live for a time t_∗ produce the LW flux and that η_LW LW photons are produced for each baryon in stars (see Greif & Bromm 2006). We then obtain for the number density n_γ of H₂-dissociating photons

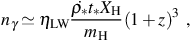(24)

where m_h is the mass of the hydrogen atom, X_h ≃ 0.76 is the fraction of baryonic mass in hydrogen, and the mass density in stars is ≃ 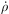_∗ t_∗. Converting this to the photon energy density u_γ = h ν n_γ, we obtain an estimate of J_LW as a function of the star formation rate per comoving volume:

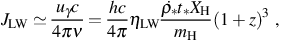(25)

where c is the speed of light. In terms of J₂₁, this is

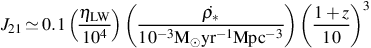(26)

where we have assumed an average lifetime t_∗ = 5 × 10⁶ yr for stars that produce the bulk of H₂-dissociating radiation (e.g. Leitherer et al. 1999; Schaerer 2002). ⁸ For a population of metal-enriched stars formed with a Salpeter-like IMF, as is inferred for the Milky Way today, η_LW ≃ 4 × 10³; however, for metal-free stellar population with a top-heavy IMF, this can be as high as η_LW ≃ 2 × 10⁴ (see e.g. Greif & Bromm 2006). In equation (26) we have normalized to an intermediate value, for simplicity; furthermore, while the star formation rate at very high redshift is not known, we have here normalized to a rough value expected in the standard ΛCDM picture of cosmological structure formation at z ≃ 10 (see e.g. Tornatore et al. 2007; Haiman 2009; Trenti & Stiavelli 2009).

A further estimate of the cosmological background J_LW, in particular that near the end of the epoch of reionization, can be found by assuming that the flux just above the Lyman limit (i.e. at hν ≥ 13.6 eV) is sufficient to reionize reionization the universe (see e.g. Bromm & Loeb 2003a; Shang et al. 2010) and that the sources producing the ionizing flux also produce a comparable flux in the LW energy range, 11.2 eV - 13.6 eV. Relating the number density of hydrogen nuclei at redshift z to the number density n_γ of ionizing photons required to keep hydrogen photoionized in the IGM, we obtain

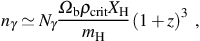(27)

where N_γ is the number of ionizing photons per hydrogen nucleus required to keep the universe reionized and Ω_bρ_crit is the cosmological average mass density of baryons at z = 0, expressed as a fraction Ω_b of the critical density ρ_crit for a flat universe. Assuming that all LW photons which are emitted from sources within galaxies escape into the IGM, and taking it that only a fraction f_esc of ionizing photons are able to escape due to the higher optical depth to photoionization, we find an estimate of the background flux as

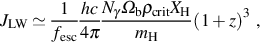(28)

where again we have converted from photon energy density u_γ = hνn_γ to units of specific intensity as in equation (25). Expressing this in terms of J₂₁, we have

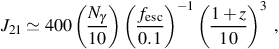(29)

where we have normalized N_γ to the value estimated by Wyithe & Loeb (2003), and f_esc is normalized to a typical value found in cosmological radiative transfer simulations (e.g. Ricotti & Shull 2000; Ciardi & Ferrara 2005; Wise & Cen 2009; Razoumov & Sommer-Larsen 2010; Yajima et al. 2011).

This estimated level of the cosmological background radiation field during reionization is well above the critical level of J₂₁ ≃ 0.04 required for suppressing the rate of Pop III star formation in minihalos, and this may have important implications for the nature of the stars that are formed. In particular, under the influence of such an elevated LW background, due to the destruction of the H₂ molecules which cool the gas, the temperature of the primordial gas when it finally collapses to form a star can be considerably higher than in the absence of a background H₂-dissociating radiation field (O'Shea & Norman 2008). This, in turn, results in a higher Jeans mass and protostellar accretion rate, likely leading to more massive Pop III stars forming in the presence of a high LW background flux.

While the LW radiation field is in general relatively uniform, near individual galaxies it can be locally higher than the cosmological average (see Dijkstra et al. 2008; Ahn et al. 2009), as shown in Figure 7. In rare regions where the LW background radiation is exceptionally high, a different outcome besides Pop III star formation in dark matter halos may result: the formation of a black hole by direct collapse (e.g. Bromm & Loeb 2003a). For this to occur, the LW radiation field must be at a level high enough to destroy molecules not just in the outskirsts of halos where the primordial gas begins to cool via emission from H₂ molecules, but also high enough to destroy H₂ even in the central dense regions of the halo (but see Begelman & Shlosman 2009; Mayer et al. 2010).

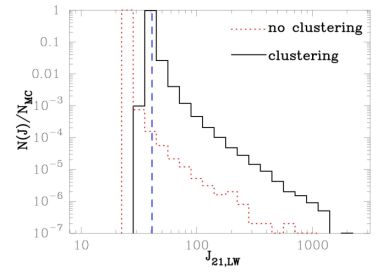Figure 7. The probability distribution of the Lyman-Werner flux JLW to which atomic cooling halos are exposed at z = 10, for a model accounting for the clustering of the galaxies which emit LW radiation (black solid histogram) and for one in which galaxies are assumed to be distributed uniformly (red dotted histogram). The mean value of the LW background found in these models is J21 ≃ 40 (dashed blue line), which is well above the level needed to suppress the rate of Pop III star formation in minihalos (see Figure 6). While rare, a small fraction of halos are exposed to a LW flux J21 ≥ 100, high enough to completely suppress star formation in atomic cooling halos until a ≥ 104 M⊙ black hole forms by direct collapse instead (see Shang et al. 2010). From Dijkstra et al. (2008).

Figure 8 shows the results of cosmological simulations from which the minimum J₂₁ required for the formation of a black hole by direct collapse can be estimated. As shown in the bottom-right panel, for J₂₁ ≥ 100 the H₂ fraction in the gas is kept to a low level at which H₂ cooling does not lower the temperature of the gas significantly below the virial temperature of T_vir ≃ 10⁴ K of the halo (Shang et al. 2010) ⁹. Therefore, when the gas finally collapses, the accretion rate of primordial gas will be very high, of the order of ≃ 0.1 M_⊙ yr⁻¹, as can be seen from equation (5). This is roughly two orders of magnitude higher than the accretion rate onto Pop III protostars formed in H₂-cooled gas at T ≃ 200 K, and the result is predicted to be an extremely massive 'quasi-star' which quickly collapses to form a black hole with a mass ≥ 10⁴ M_⊙ (e.g. Bromm & Loeb 2003a; Koushiappas et al. 2004; Begelman et al. 2006; Spaans & Silk 2006; Lodato & Natarajan 2006; Regan & Haehnelt 2009; et al. 2010b). While this level of the background LW radiation field is expected to be higher than the average, as shown in Figure 7, due to the clustering of the stars and galaxies producing LW radiation there may be a significant number density of black holes formed by direct collapse in the early universe. Indeed, some of these may be the seeds of the supermassive black holes observed at z ≤ 6 (see e.g. Haiman 2009).

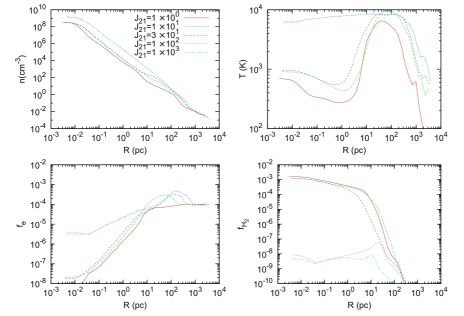Figure 8. Properties of the primordial gas in a cosmological simulation, for various elevated levels of the LW background radiation field JLW, here assumed to be produced by stars with an effective surface temperature 104 K, as is appropriate for metal-enriched Pop II stars. Clockwise from top left: number density, temperature, H2 fraction, and free electron fraction, each shown as a function of the distance from the center of an atomic cooling halo. A LW flux with J21 ≥ 100 can prevent the formation of a sufficient fraction of H2 to cool the gas below ≃ 6 × 103 K, even at very high densities. Due to the large Jeans mass (equation 4) and accretion rate (equation 5) this implies, instead of hosting Pop III star formation, atomic cooling halos which are exposed to such an intense LW flux are likely to host the formation of a ≥ 104 M⊙ black hole by direct collapse. From Shang et al. (2010).

2.3. The Impact of Radiation from Accreting Black Holes on the Primordial Gas

In addition to the radiation emitted by the first generations of stars, black holes formed and assembled into the first galaxies can also produce radiation which dramatically impacts the primordial gas. In particular, the effects of the radiation emitted from black holes formed by direct collapse can be especially strong, as there is an initially large reservoir of gas that can be accreted onto the nascent black hole (see Johnson et al. 2011). To draw a comparison between the radiation emitted from stars in the first galaxies to that emitted during the accretion of gas onto black holes, we can calculate the temperature of the accretion disk and compare it to the typical effective temperature of a star. For a steady accretion flow, the temperature T of the accretion disk can be estimated by balancing the rate at which the disk is heated with the rate at which it cools. The heating is due to the gravitational potential energy of matter falling through the disk being dissipated by viscosity; for material falling through the disk and onto the black hole at a rate _BH, the resultant heating rate per unit area Γ of the disk can be estimated on dimensional grounds as (e.g. Pringle 1981)

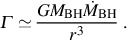(30)

Assuming the disk is optically thick, then the rate at which the disk cools per unit area Λ can be estimated using the Stefan-Boltzmann law: Λ = σ_SB T⁴, where σ_SB the Stefan-Boltzmann constant. Equating these rates yields a temperature profile for the disk. The profile thus obtained is very close to the following formal solution, but for a correction near the inner edge of the disk r_in where the viscous heating rate goes to zero:

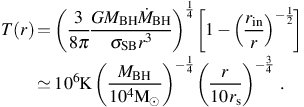(31)

In the second part of the equation we have normalized to a black hole mass of 10⁴ M_⊙, appropriate for the initial mass of a black hole formed by direct collapse. We have also normalized the radius to 10 Scharzschild radii r_s = 2GM_BH / c², which is well outside the inner edge of the accretion disk, r_in ≤ 3r_s. Finally, we have assumed accretion to take place at the Eddington rate _Edd, at which the outward force due to electron scattering of the emitted radiation balances the inward gravitational force acting on the accreting gas:

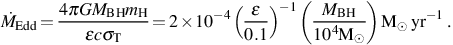(32)

Here σ_T = 6.65 × 10⁻²⁵ cm² is the Thomson cross section for the scattering of photons off electrons, and є is the ratio of the radiated energy to the rest mass energy of the accreting material, normalized to a value appropriate for a slowly rotating black hole.

Figure 9. The projected number density (left panel), temperature (middle panel), and H ii fraction (right panel) of the gas in the vicinity of an accreting 2.5 × 104 M⊙ black hole formed by direct collapse in an atomic cooling halo at z ∼ 12. The ionizing radiation emitted from the accretion disk of the black hole has a strong impact on the gas in the halo, heating it to temperatures ≃ 3 × 104 K and causing expansion and disruption of the dense gas in the center of the halo from which the black hole feeds. From Johnson et al. (2011).

As shown in equation (31), the temperature near the inner edge of the accretion disc of a rapidly accreting black hole can be as high as T ≃ 10⁷ K. This is much higher than the effective temperature of even a very massive Pop III star, which is roughly two orders of magnitude lower. In turn, this implies that accreting black holes in the first galaxies emit both copious ionizing radiation and substantial LW radiation, as well as high energy X-rays (see e.g. Ricotti & Ostriker 2004; Kuhlen & Madau 2005). In the case of a black hole formed by direct collapse, the resultant photoheating of the gas in the host atomic cooling halo can drive its temperature to ≃ 3 × 10⁴ K, as shown in Figure 9 (Johnson et al. 2011). Along with the associated high radiation pressure, this results in the expansion of the gas surrounding the black hole. The resultant drop in the density of the accreting gas translates into a decrease in the accretion rate of the black hole, which can be estimated by assuming gas which is gravitationally bound to the black hole falls towards it at the sound speed (see e.g. Bondi 1952). With the radius within which gas is bound to the black hole given by r_B = 2GM_BH / (c_s² + v_BH²), where v_BH is the velocity of the black hole relative to the gas, the accretion rate is estimated as the rate at which mass passes within a distance r_B of the black hole:

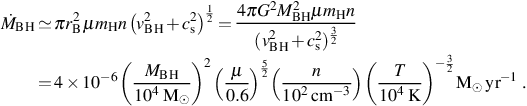(33)

In the second part of the equation we have assumed a black hole at rest with respect to the gas (v_BH = 0) and we have again related the gas temperature to the sound speed using 3k_B T/2 = µ m_h c_s² / 2. As the accretion rate is directly proportional to the density of the accreting gas and inversely proportional to its temperature, that the high energy radiation emitted from the accretion disk acts to heat and rarify the gas means that the accretion rate itself is regulated by the radiation generated in the process. Indeed, the Eddington rate given by equation (32) provides an estimate of the maximum rate at which gas can be accreted in the face of the intense radiation that is emitted. However, hydrodynamics calculations of accretion onto black holes formed in the first galaxies suggest that _BH is on average well below the Eddington rate because of both strong radiative feedback during accretion (see e.g. Pelupessy et al. 2007; Alvarez et al. 2009; Milosavljević et al. 2009; Park & Ricotti 2010; Johnson et al. 2011) and low gas densities (e.g. Yoshida 2006; Johnson & Bromm 2007). This poses a challenge for the rapid growth of black holes in the early universe.

A further challenge to the model of black hole formation by direct collapse is the enrichment of the primordial gas with the first heavy elements (e.g. Omukai et al. 2008; Safranek-Shrader et al. 2010), which can easily cool the gas more efficiently than either H₂ or HD molecules. We turn next to the broader question of how the first supernovae, which enrich the gas, transform the process of star formation in the first galaxies.

³ We use the common term 'metals' to refer to elements heavier than helium which are produced in stars and supernovae. Back.

⁴ Due to infrequent particle collisions at low densities, the rate of radiative deexcitations can exceed that of collisional deexcitations, leading to non-LTE level populations (see Section 3.3). Back.

⁵ As H⁺ is also referred to as H ii, such photoionized regions formed around stars are called H ii regions. Likewise, the radiation from massive stars, and especially massive Pop III stars, can doubly ionize helium within the so-called He iii region (see Section 4). Back.

⁶ Before the adoption of this terminology, Pop III.2 was formerly referred to as Pop II.5 in the literature (e.g. Mackey et al. 2003; Johnson & Bromm 2006). Back.

⁷ While for simplicity we limit our discussion to the photodissociation of H₂, HD molecules are also destroyed via this mechanism. Back.

⁸ Also note that in going from the flux estimate given by equation (25) to equation (26) we have accounted for the ≃ 2.4 eV spread in LW photon energies, which is not explicitly included in equation (25). Back.

⁹ It is important to note that the spectrum of the radiation producing the LW background must also be taken into account. While the results shown in Figure 8 are derived under the assumption that the LW background is generated by stars with an effective surface temperature of 10⁴ K, appropriate for Pop II stars, higher levels of the LW flux are required to suppress H₂ formation if, for instance, it is generated by massive Pop III stars with effective surface temperatures of ≃ 10⁵ K (see e.g. Shang et al. 2010). Back.