

During the last decade, cosmology has advanced from an era of largely qualitative questions — is the Universe flat, open or closed?, does dark energy exist in the Universe?, etc. — to one where precision determinations of many of the Universe's properties are possible. We have cosmological models capable of explaining the detailed observations available, and whose parameters are beginning to be pinned down at the ten percent, and in some cases one percent, level [1]. Nevertheless, quality cosmological data are an expensive resource and it is imperative to make the best possible use of them. This implies use of the best available statistical tools in order to obtain accurate and robust conclusions.
For around a decade now, the established leading cosmological model considers five material constituents: baryons (taken, imprecisely, to include electrons), photons, neutrinos, cold dark matter (CDM), and dark energy. The simplest model for dark energy, a cosmological constant Λ, is in excellent agreement with observations, and the model is then known as a ΛCDM model. The most important constraints come from the evolution of cosmic structures. These are seeded by small initial density perturbations, which in the standard cosmological model are taken as adiabatic, gaussian, and nearly scale-invariant, as predicted by the simplest models of cosmological inflation [2].
This model is supported and constrained by a series of cosmological observations. Most important are measurements of cosmic microwave background (CMB) anisotropies, particularly by the Wilkinson Microwave Anisotropy Probe (WMAP) as shown in Figure 1. Typical analyses also incorporate other data, such as galaxy clustering data, the luminosity distance–redshift relation of Type Ia supernovae, and direct measures of the Hubble constant. The region of parameter space where the ΛCDM model matches all those data is often referred to as the concordance model.
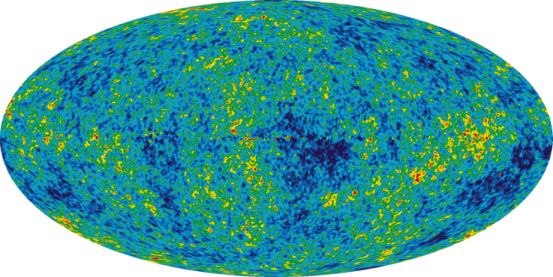 |
Figure 1. Cosmic microwave background anisotropies as imaged by WMAP from five years of accumulated data. [Figure courtesy NASA/WMAP Science Team.] |
In its very simplest incarnation, the photon density is taken to be well measured by the CMB temperature, neutrinos to be nearly massless, and the Universe spatially flat. The model then features only four fundamental parameters: the Hubble parameter h, the densities of baryons Ωb and CDM ΩCDM, and the amplitude of primordial density perturbations AS. In addition, a comparison with data will usually include extra phenomenological parameters, which in principle can be computed from the above but which in practice cannot be reliably. For cosmic microwave background studies, the optical depth τ, measuring the fraction of CMB photons scattering from ionized gas at low redshift, is needed, while use of galaxy clustering data may require inclusion of the galaxy bias parameter b which relates galaxy clustering to dark matter clustering.
Beyond those basic parameters, cosmologists hope that future investigations will uncover new physical processes, permitting extra parameters to be incorporated and measured. In some cases, it is more or less certain that the parameter is relevant and only a matter of time before observational sensitivity becomes sufficient. Examples here are neutrino masses and the cosmic Helium fraction (though the latter is again in principle computable from other parameters, independent verification of its value would be an important consistency check).
Much more numerous, though, are parameters describing effects which may or may not be relevant to our Universe. An extensive list is given, for instance, in Ref. [3]. Are the primordial perturbations precisely scale invariant, or do they have a scale dependence quantified by the spectral index n? Do primordial gravitational waves exist, as predicted by inflation? Does the dark energy density evolve with time? Are there cosmic strings in the Universe? Are the initial perturbations really adiabatic and gaussian? A fuller account of these parameters can be found for instance in Ref. [4].
In summary, creation of precision cosmological models is an ongoing process with two distinct goals. One is to determine the set of parameters, i.e. physical processes, necessary to describe the available observations. The second is to determine the preferred values of these parameters. We can then pursue the ultimate aim of relating cosmological observations to underlying fundamental physics.