A fourth prong of the hunt for dark matter is the search to discover dark stars. The first stars to form in the universe, at redshifts z ∼ 10−50, may be very unusual; these dark stars are made almost entirely of atomic matter (hydrogen and helium, with only 10−3 of the mass made of dark matter) and yet are powered by dark matter heating rather than by fusion. Dark stars were first proposed by Spolyar, Freese, and Gondolo [94] and are reviewed in Ref. 95.
As discussed in the last section, WIMP dark matter annihilation in the early universe provides the right abundance today to explain the dark matter content of our universe. This same annihilation process will take place at later epochs in the universe wherever the dark matter density is sufficiently high to provide rapid annihilation. The first stars to form in the universe are a natural place to look for significant amounts of dark matter annihilation, because they form at the right place and the right time. They form at high redshifts, when the universe was still substantially denser than it is today, and at the high density centers of dark matter haloes.
The first stars form inside dark matter haloes of ∼ 106 M⊙ (for reviews see e.g., Ripamonti & Abel, [98] Barkana & Loeb, [96] and Bromm & Larson; [97] see also Yoshida et al. [99]). One star is thought to form inside one such dark matter halo. It was our idea to ask, what is the effect of the dark matter on these first stars? We studied the behavior of WIMPs in the first stars. As our canonical values, we take mχ = 100 GeV for the WIMP mass and ⟨ σ v ⟩ann = 3 × 10−26 cm3 / sec for the annihilation cross section (motivated above). However, the same behavior results for a wide variety of WIMP masses and cross sections over many orders of magnitude. We find that the annihilation products of the dark matter inside the star can be trapped and deposit enough energy to heat the star and prevent it from further collapse. A new stellar phase results, a dark star, powered by dark matter annihilation as long as there is dark matter fuel.
6.1. Three Criteria for Dark Matter Heating
WIMP annihilation produces energy at a rate per unit volume
 |
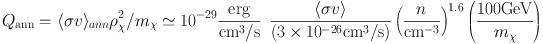(14) |
where ρχ is the dark matter energy density inside the star and n is the stellar hydrogen density. Spolyar, Freese and Gondolo [94] outlined the three key ingredients for dark stars: 1) high dark matter densities, 2) the annihilation products get stuck inside the star, and 3) dark matter heating wins over other cooling or heating mechanisms. These ingredients are required throughout the evolution of the dark stars.
First criterion: high dark matter density inside the star. Dark matter annihilation is a powerful energy source in these first stars because the dark matter density is high. To find the dark matter density profile, we started with an NFW (Navarro, Frenk & White [100]) profile for both dark matter and gas in the 106 M⊙ halo. However, we find the same behavior results for even a completely flat profile; the dark star is born regardless. Originally we used adiabatic contraction (M(r)r = constant) (Blumenthal et al. [101]) and matched onto the baryon density profiles given by Abel, Bryan & Norman [102] and Gao et al. [103] to obtain dark matter profiles; see also Natarajan, Tan & O'Shea [104] for a recent discussion. Subsequent to our original work, we have done an exact calculation (which includes radial orbits) (Freese, Gondolo, Sellwood & Spolyar [105]) and found that our original results were remarkably accurate, to within a factor of two. At later stages, we also consider possible further enhancements due to capture of dark matter into the star (discussed below).
Second Criterion: dark matter annihilation products get stuck inside the star. In the early stages of Population III star formation, when the gas density is low, most of the annihilation energy is radiated away (Ripamonti, Mapelli & Ferrara [106]). However, as the gas collapses and its density increases, a substantial fraction fQ of the annihilation energy is deposited into the gas, heating it up at a rate fQ Qann per unit volume. While neutrinos escape from the cloud without depositing an appreciable amount of energy, electrons and photons can transmit energy to the core. We have computed estimates of this fraction fQ as the core becomes more dense. Once n ∼ 1011 cm−3 (for 100 GeV WIMPs), e− and photons are trapped and we can take fQ ∼ 2/3.
Third Criterion: dark matter heating is the dominant heating/cooling mechanism in the star. We find that, for WIMP mass mχ = 100 GeV (1 GeV), a crucial transition takes place when the gas density reaches n > 1013 cm−3 (n > 109 cm−3). Above this density, dark matter heating dominates over all relevant cooling mechanisms, the most important being H2 cooling (Hollenbach & McKee [107]).
Fig. 11 shows evolutionary tracks of the protostar in the temperature-density phase plane with dark matter heating included (Yoshida et al. [108]), for two dark matter particle masses (10 GeV and 100 GeV). Moving to the right on this plot is equivalent to moving forward in time. Once the black dots are reached, dark matter heating dominates over cooling inside the star. The protostar collapses somewhat further until it reaches equilibrium, at which point the dark star phase begins. The protostellar core is prevented from cooling and collapsing further. The size of the core at this point is ∼ 17 A.U. and its mass is ∼ 1 M⊙ for 100 GeV mass WIMPs. A new type of object is created, a dark star supported by dark matter annihilation rather than fusion.
 |
Figure 11. Temperature (in degrees K) as a function of hydrogen density (in cm−3) for the first protostars, with dark matter annihilation included, for two different dark matter particle masses (10 GeV and 100 GeV). Moving to the right in the figure corresponds to moving forward in time. When the “dots” are reached, dark matter annihilation wins over H2 cooling. After that the protostar collapses somewhat further until it reaches equilibrium. At that point a dark star is created. |
We have found the stellar structure of the dark stars (hereafter DS) (Freese, Bodenheimer, Spolyar & Gondolo [109]). They accrete mass from the surrounding medium. We built up the DS mass as it grows from ∼ 1 M⊙ to possibly become supermassive. The studies were done in two different ways, first assuming polytropic interiors and more recently using the MESA stellar evolution code; the basic results are the same. [122] As the mass increases, the DS radius adjusts until the dark matter heating matches its radiated luminosity. We find solutions for dark stars in hydrostatic and thermal equilibrium. We build up the DS by accreting 1 M⊙ at a time with a variety of possible accretion rates, always finding equilibrium solutions. We find that initially the DS are in convective equilibrium; from (100−400) M⊙ there is a transition to radiative; and heavier DS are radiative. As the DS grows, it pulls in more dark matter, which then annihilates. Fig. 12 shows the hydrogen and dark matter density profiles. One can see “the power of darkness”: although the dark matter constitutes a tiny fraction (< 10−3) of the mass of the DS, it can power the star. The reason is that WIMP annihilation is a very efficient power source: 2/3 of the initial energy of the WIMPs is converted into useful energy for the star, whereas only 1% of baryonic rest mass energy is useful to a star via fusion.
 |
Figure 12. Evolution of a dark star as mass is accreted onto the initial protostellar core of 3 M⊙. The set of upper (lower) curves correspond to the baryonic (dark matter) density profile at different masses and times. Note that dark matter constitutes < 10−3 of the mass of the DS. |
The dark stars will last as long as the dark matter fuel inside them persists. Once the gravitationally attracted dark matter runs out, the star collapses somewhat, at which point the star is dense enough to capture more dark matter.
The new source of dark matter in the first stars is capture of dark matter particles from the ambient medium. Any dark matter particle that passes through the DS has some probability of interacting with a nucleus in the star and being captured. The new particle physics ingredient required here is a significant scattering cross section between the WIMPs and nuclei. Whereas the annihilation cross section is fixed by the relic density, the scattering cross section is a somewhat free parameter, set only by bounds from direct detection experiments. Two simultaneous papers (Freese, Spolyar & Aguirre, [110] Iocco [111]) found the same basic idea: the dark matter luminosity from captured WIMPs can be larger than fusion for the DS. Two uncertainties exist here: the scattering cross section, and the amount of dark matter in the ambient medium to capture from. DS studies following the original papers that include capture have assumed (i) the maximal scattering cross sections allowed by experimental bounds and (ii) ambient dark matter densities that are never depleted. With these assumptions, DS evolution models with dark matter heating after the onset of fusion were studied in several papers. [112, 113]
Dark stars are very unusual stars — they are made of atomic matter (hydrogen and helium) but they are powered by dark matter heating (Freese, Bodenheimer, Spolyar & Gondolo [109]). They are very puffy (10 A.U. in size) and cool (surface temperatures ∼ 10,000 K. Reionization during this period is likely to be slowed down, as these stars can heat the surroundings but not ionize them. Because they are so cool, they can keep accreting matter and growing as long as there is dark matter fuel. Standard Population III stars are hot, give off ionizing photons, and prevent further accretion above ∼ 140 M⊙. Dark stars, on the other hand, can keep growing to become supermassive, even as massive as 107 M⊙ and as bright as 1010 L⊙. There should be a variety of dark star masses ranging from a few solar masses all the way up to these very large masses.
Fig. 13 shows the Hertzsprung-Russell diagram for dark stars as they grow from ∼ 1 M⊙ to become supermassive. The two cases of matter being accreted gravitationally and via capture are shown separately.
 |
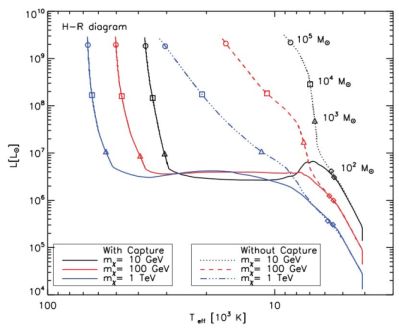Figure 13. Hertzsprung-Russell diagram for DSs for a variety of WIMP masses as labeled for the two cases: (i) with gravitationally attracted dark matter only (dotted lines), assuming no significant depletion of dark matter due to annihilation, which is equivalent to assuming a replenishment of dark matter due to centrophilic orbits; (ii) with capture (solid lines). Results were obtained assuming polytropic interiors for the DS. The case with capture is for product of scattering cross section times ambient WIMP density σc ρχ = 10−39 GeV/cm3 (the maximum allowed cross section for all WIMP masses and the maximum reasonable ambient density for 100 GeV WIMPs). Once the gravitational dark matter runs out, DSs must first become dense enough in order for dark matter capture to happen. This explains the horizontal lines in the evolution of the case with capture. Labeled are also stellar masses reached by the DS on its way to becoming supermassive. The final DS mass was taken to be 105 M⊙ (the baryonic mass inside the initial halo), but could vary from halo to halo, depending on the specifics of the halo mergers (figure taken from Ref. 114). |
6.5. Dark Stars are Detectable in James Webb Space Telescope
Supermassive dark stars may be detectable in the JWST as J, H, or K-band dropouts. Detailed discussion may be found in Refs. 114, 115, 116. Comparison of light output with sensitivity of JWST filters is shown in Fig. 14 for a 106 M⊙ DS. Predictions for numbers of these objects, based on cosmological simulations, is also found in Ref. 114.
 |
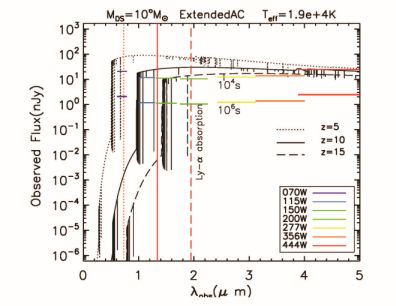Figure 14. Supermassive Dark Stars in JWST. Spectra for 106 M⊙ supermassive DSs formed at redshift zform = 15 compared with sensitivity of JWST filters. The formation mechanism in this figure is gravitational attraction of dark matter only. The surface temperature Teff = 1.9 × 104 K. The fluxes are shown at z = 15 (dashed line), 10 (solid line) and 5 (dotted line) and compared to the detection limits of NirCam wide passband filters. The colored horizontal lines represent the sensitivity limits for the filters as labeled in the legend for exposure times 104 sec (upper lines) and 106 sec (lower lines). IGM absorption will decrease the observed fluxes for wavelengths shortward of the vertical red lines, which indicate the Lyman-α line (1216 Angstroms) redshifted from the rest-frame of the star (figure taken from Ref. 116). |
Once these supermassive dark stars (SMDS) run out of dark matter fuel, they collapse to black holes. They may provide large seeds for the supermassive black holes that have been found at high redshift (109 − 1010 M⊙ BH at z = 6) and are, as yet, unexplained (Li et al., [119] Pelupessy et al., [120] Wu et al. [121]).
An interesting new research direction is the fact that DS pulsate, like all stars. As a first step, we used the MESA stellar evolution code to calculate the adiabatic pulsation periods of radial p-modes (where the restoring force is pressure and those for which there is no angular dependence, so l = 0). We found that our DS models pulsate on timescales which range from less than a day to more than two years in their restframes at about z = 15, depending on the WIMP mass and overtone number. The pulsation periods are significantly shorter for higher WIMP mass. Converting to the observer frame, the shortest periods we found are less than about 50 days for modes with overtone number n > 6 and a WIMP mass of 1 TeV (Ref. 122). We are currently investigating other pulsation modes: nonadiabatic modes and also dark matter density driven modes.
In short, the first stars to form in the universe may be dark stars powered by dark matter heating rather than by fusion. Our work indicates that they may become very large (up to 107 M⊙) and bright (up to 1010 L⊙), thereby detectable in upcoming JWST observations. They may provide seeds for the many supermassive black holes found in the universe. The observational possibilities of discovering dark matter by finding these stars with JWST data is intriguing. Further, once DS are found, one can use them as a tool to study the properties of WIMPs.