Measuring absolute luminosities of galaxies that are distance-independent
to a high precision is important for a wide range of astronomical
applications (e.g., sizes of galaxies, black hole masses, total galaxy
mass measurements etc). Tonry and collaborators have discovered a
further parameterisation of the SBF method
(T01).
Moreover, this description is not only distance-independent but also
independent from the photometric calibration or dust extinction. The
parameter N is
defined as the ratio of
the total apparent flux from a galaxy to the flux provided
by the fluctuation signal. In terms of magnitudes, this (absolute
luminosity) measure is the difference between the fluctuation magnitude
and the total magnitude of the galaxy
tot,
which corresponds to the total luminosity of the galaxy in units of the
luminosity of a typical giant star within that galaxy as:
 |
(10) |
N is also referred to as the ‘fluctuation star count’.
As expected, galaxy colour correlates with N (which is a proxy for the absolute luminosity) following the relation:
 |
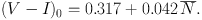(11) |
Figure 9 shows the dependence of the (V − I) galaxy colour on the fluctuation star count N. The correlation is well established for different morphological types (E, S0, Sa) and across a range of luminosities. The relation in equation 11, which is shown in Figure 9 as the solid and dotted ( ± 1σ error) lines, is slightly steeper but in good agreement with the correlation of N and (V − I) found by T01 (dashed line).
 |
Figure 9. (V − I)0 galaxy colour as a function of the fluctuation star count NI for different morphological types (Blakeslee et al. 2001b). Symbols are as in Figure 4. The dashed line is the empirical relation from Tonry et al. (2001). |
Surprisingly, the slope of this relation is very shallow with an observed scatter in (V − I) of 0.04 mag. Therefore, a large error in N translates into a negligible effect in (V − I); for example assuming δN = 0.5 mag corresponds to only δ(V − I) = 0.016 mag (T01). According to the prediction, the intrinsic scatter of the relation might be as small as 0.025 mag, which also suggests that it is an efficient way of deriving accurate extinction measurements with rms uncertainties of 2%.
Although there is some covariance from the application of
I
for both the distance modulus and the intrinsic galaxy colour, the actual
covariance is very mild because of the shallow slope of the
N −
(V − I) relationship. Instead, using the galaxy
colour to estimate
I
directly is challenging due to the observational requirements of
high-precision photometry and the accurate assessment of the presence of
and sensitivity to dust extinction.
Based on the I-band SBF survey,
T01 found an empirical
relationship between
I and
N following
 |
(12) |
Although this introduces a covariance between
I derived in this
way and I,
the resulting distance modulus is 14% less sensitive
to (systematic) uncertainties in
I
(Blakeslee et al. 2001b).
However, N should
be not regarded as a substitute for (V − I)
when deriving I,
as the parameter is still relatively
unexplored. Nevertheless, in the absence of a galaxy colour,
N
provides an alternative way to measure a distance. For example,
Cantiello et al. (2011)
have adopted a calibration based on
N to derive the
distance to 12 nearby galaxies with an accuracy
of about 30%, where colour information was unavailable in the data archive.
The consequence of the relationship of
N with
I
is suggested to rely on the Fundamental Plane of early-type galaxies
(Djorgovski & Davis
1987;
Dressler et al. 1987)
and their projections (e.g.,
Fritz et al. 2005;
2009a).
If a colour measurement is available,
N should not supplant
the application of (V − I) to calibrate
I.
Nevertheless, it appears that
N offers a valuable
alternative to measure a fairly reliable distance, but more work is
needed to understand the parameter and its relatively large scatter
fully.