Annu. Rev. Astron. Astrophys. 2017. 55: 59-109 Copyright © 2017 by Annual Reviews. All rights reserved

3. THE NEED FOR ACCURATE MODELLING OF THE GALACTIC INTERSTELLAR MEDIUM AND 'FEEDBACK'

The large differences of sub-resolution models presented in the previous section are noteworthy but also a bit worrying as the models should be representations of the same underlying physical processes. Many groups have been able to design and callibrate feedback procedures that allow them to more or less successfully match the present day galaxy mass function, or more accurately, the ratio of dark matter to galaxy masses, the cosmological evolution of galaxy abundances, and the evolution in galaxy sizes and stellar populations (the Eagle project seems to have done this most successfully). In Fig. 4 you can assess to which level the different groups have succeeded in this calibration to present day galaxy mass functions similar to the one presented in Li & White (2009). With the large conceptual differences in the respective feedback models the good (or not so good) agreement with the observed mass function can be attributed to a more or less successful tuning of the normalizations and scalings in the sub-resolution models. The theoretical predictions are stellar mass functions from large scale cosmological simulations in recent publications: from Davé et al. (2013) using traditional SPH, 'energy and momentum driven' decoupled winds and a heuristic model for gas heating in massive halos (no AGN feedback); from Davé, Thompson & Hopkins (2016) sing a meshless finite mass method with star formation feedback scaling motivated by higher resolution simulations and an improved empirical gas heating model to Davé et al. (2013) for massive halos; from Puchwein & Springel (2013) using traditional SPH with momentum driven winds and thermal and 'bubble' AGN heating; from Dubois et al. (2014) (Horizon-AGN) with AMR, mechanical supernova feedback, thermal AGN feedback with variable boost factor and jet-feedback for low accretion rates, from Vogelsberger et al. (2014) (the Illustris simulations) with a moving mesh code, decoupled 'momentum driven' winds, thermal and 'bubble' AGN heating and radiation input from the AGN; Schaye et al. (2015) (the Eagle simulations) with improved SPH, 'stochastic thermal' heating from stars and AGN; from Hirschmann et al. (2014) (the Magneticum simulations) with traditional SPH, constant winds, thermal AGN heating and a modified 'bubble' heating; from Khandai et al. (2015) (the MassiveBlack II simulations) with traditional SPH, 'decoupled wind' and thermal AGN feedback. The simulations have more or less succeeded in this exercise. For comparison we show a (typical) observed galaxy mass function in the local Universe (Li & White 2009). Again, we point out that such a mass function is used for most simulations and alternative mass functions take extended stellar mass distributions in massive galaxies into account (Bernardi et al. 20113). Even with the significant differences in the sub-grid model assumptions it seems that many simulations capture the basic characteristics. Still to be achieved are cosmological simulations yielding good matches to galaxy population properties on the basis of numerically resolved ab initio physical modeling of feedback processes.

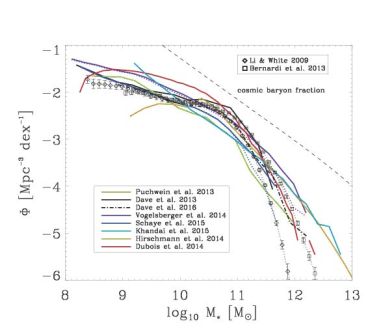Figure 4. Comparison of galaxy stellar mass functions from recent large scale cosmological simulations of representative volumes of the Universe (see text). The simulations include stellar and AGN feedback with the exception of Davé et al. (2013) who use an empirical heating model in massive halos. The different groups typically adjust the key parameters in the varying sub-resolution models to match observations of galaxy mass functions like the one of Li & White (2009). For reference we show an alternative mass function with different mass estimates for massive galaxies (Bernardi et al. 2013). At a given mass the abundance can vary by up to an order of magnitude, still considering the range in spatial resolution (from 0.5 kpc to 3 kpc) and the significant difference in sub-resolution models the agreement between the simulations is remarkable for some models. The dashed line for Vogelsberger et al. (2014) and Schaye et al. (2015) indicate different mass estimates. The dashed line shows the hypothetical galaxy mass function assuming the cosmic baryon fraction.

3.1. Supernova explosions

Core-collapse supernova explosions have for long been the primary suspect to play a crucial role in galaxy formation (Larson 1974, Dekel & Silk 1986, Navarro & White 1993). During these singular and final events in a massive star's live typically 2 - 5 M_⊙ of gas are ejected into the ambient interstellar medium (ISM) at supersonic velocities of v_eject ∼ 6000 − 7000 km s⁻¹ (Janka 2012) driving a shock into the ambient ISM. Apart from the injection of metals, supernovae can - in the energy conserving phase of the blast wave - heat about three orders more ambient mass than their ejecta to high temperatures. This makes them the prime ources of hot (T ∼ 10⁶ K) gas in the star forming ISM. By creating the hot, X-ray emitting, phase they impact the large-scale multi-phase structure of the ISM (McKee & Ostriker 1977, Walch et al. 2015, Li et al. 2015) and might be important for driving galactic outflows, fountain flows, and galactic winds through hot, low density, chimneys (Norman & Ikeuchi 1989, Chevalier & Clegg 1985, Heckman, Armus & Miley 1990, Strickland & Stevens 2000, Heckman 2003, Joung & Mac Low 2006, Hill et al. 2012, Hennebelle & Iffrig 2014, Girichidis et al. 2016b). The momentum injected by supernovae contributes to the kinetic energy content of the ISM. With pure momentum injection simulations it has been argued that supernovae can create realistic turbulence (see reviews on ISM turbulence by Elmegreen & Scalo 2004, Scalo & Elmegreen 2004) in the warm and cold ISM and regulate the scale heights of galactic disks (by large scale turbulent pressure) as well as their star formation rates (see Ostriker & Shetty 2011, Kim & Ostriker 2015b).

The importance of supernova explosions for setting the ISM structure motivates a more detailed review of the different phases of supernova blast waves (see also Chevalier 1982, Ostriker & McKee 1988, Cioffi, McKee & Bertschinger 1988, Blondin et al. 1998, Draine 2011, Kim & Ostriker 2015a, Haid et al. 2016). The direct momentum of supernova ejecta is insufficient to accelerate a significant amount of gas to high velocities in the early free expansion phase. Once the supernova ejecta have swept up cold interstellar material of comparable mass the remnant enters the energy conserving Sedov-Taylor phase (Sedov 1959, Taylor 1960, Truelove & McKee 1999). In this phase about 1000 times the ejecta mass is heated and about 10 times the initial (ejecta) radial momentum can be generated as long as the temperature changes are dominated by adiabatic expansion (this can amount to 100 times the ejecta momentum in the absence of cooling). As soon as radiative losses become dominant a cooling shell forms and the amount of hot gas decreases rapidly. Analytical estimates for the time t_sf, radius r_sf, velocity v_sf, temperature T_sf, mass M_sf, and radial momentum p_sf at shell formationas a function of explosion energy E₅₁ in units of 10⁵¹ ergs, and the number density of a homogenous ambient medium in cm⁻³ result in the following relations (taken from Kim & Ostriker 2015a, but see also Draine 2011):

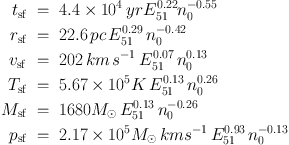(3) (4) (5) (6) (7) (8)

Kim & Ostriker (2015a) have shown in detail that these analytic estimates agree well with direct, high-resolution, three-dimensional numerical simulations (see also (Walch & Naab 2015, Iffrig & Hennebelle 2015, Martizzi, Faucher-Giguère & Quataert 2015).

After shell formation the supernova enters a short transition phase and the following pressure driven snowplow phase is powered by the homogenous pressure inside the shell. Once all excess thermal energy is radiated away, no radial momentum can be generated any more and the remnant enters the momentum conserving snowplow phase. Travelling into the interstellar medium the shock wave transforms into a sound wave (when the expansion velocity reaches the sound speed of the interstellar medium) and fades away. It can be shown that for solar neighborhood conditions an initially uniform medium will be completely changed within 2Myrs by overlapping remnants in their fade-away stage (Draine 2011). This simple argument indicates that supernovae alone might determine the thermal and dynamical state of the ISM (McKee & Ostriker 1977). Subsequent to this phase supernova remnants will propagate in the multi-phase medium with greater efficiency and reduced losses. These properties have yet to be fully assimilated into cosmological simulations of galaxy formation.

Radiative cooling, i.e. the actual ambient density and metallicity at the time of the supernova explosions, determines the duration of the momentum generating phases of which the Sedov-Taylor phase is the most important. For single supernovae exploding in ambient densities of ∼ 100 − 0.1 cm⁻³ cooling becomes dominant after about ∼ 10⁴ − 10^5.5 years limiting the momentum generation to factors of ∼ 10 − 30 (Haid et al. 2016). For reliable simulations of the galactic ISM it is important that the momentum generating phases of supernovae remnants can be captured accuratly. While analytic estimates are useful for homogeneous ambient media they cannot simply be applied to the more complex multi-phase structure of a realistic ISM. Here, numerical simulations have made a significant progress in recent years. We discuss this effort a bit more in detail as we think it is a good example of how resolved numerical simulations with different simulation codes can be used to understand a specific relevant physical process in more complex environments.

In Fig. 5 we show an overview of mostly three-dimensional numerical simulations measuring the momentum injection into the interstellar medium for the various conditions of the ambient ISM. Martizzi, Faucher-Giguère & Quataert (2015) have used the adaptive mesh refinement code RAMSES for homogeneous ambient medium and one with a lognormal density distribution representing a Mach 30 turbulent ISM. The simulations of bKim & Ostriker (2015b) have been performed with the ATHENA code for a homogenous and a structured two-phase medium (cold and warm phase). Additional simulations for a three-phase medium have been performed by Li et al. (2015) with the AMR code ENZO. We have to note that even at low resolution the total mometum input of a supernova can be correctly computed. However, the swept up mass and the velocity of the shell can still be incorrect (Hu et al. 2016).

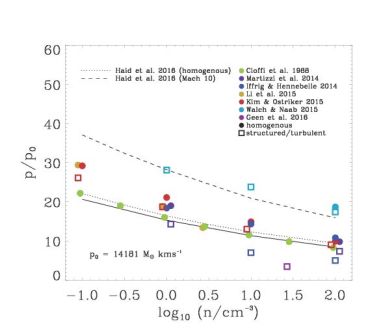Figure 5. Momentum generated in radiative supernova remnants for various ambient densities normalized by a fiducial initial momentum of p0 = 14181 M⊙ km s−1 for an explosion energy of 1051 erg and two solar masses ejecta. The analytically derived momentum at shell formation (Eqn. 8, solid line) terminates the energy conserving Sedov-Taylor phase (Kim & Ostriker 2015a) and the momentum can increase a bit more until the beginning of the momentum conserving snowplow phase (dotted line). The dashed line indicates the momentum injection for an analytical model of a log-normal (Mach 10) density distribution (Haid et al. 2016). Colored symbols show results from three dimensional numerical simulations (with the exception of the one-dimensional simulations by Cioffi, McKee & Bertschinger 1988) with homogenous, structured or turbulent ambient media carried out with three different grid codes and a particle based SPH code.

A supernova does not only inject momentum into the ISM. It also generates hot gas in the early phases of the remnant's evolution. The maximum amount of hot gas is reached at the time of shell formation, marking the end of the Sedov-Taylor phase. If no other supernova explodes within the remnant's radius until the time of shell formation T_sf the remnant will cool rapidly and no stable hot phase can be generated. For a homogenous ISM of density n₀ and a given supernova rate density S we can estimate the expectation value N_hot for a supernova to explode in a hot phase within the shell formation radius r_sf:

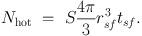(9)

With Eqns. 4 and 7 this results in

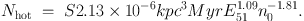(10)

For a typical gas surface density similar to the solar neighborhood of 10 M_⊙ pc⁻² the Kennicutt relation (Kennicutt 1998) gives an observed star formation rate surface density of 7 × 10⁻² M_⊙ yr⁻¹ kpc⁻². With a Salpeter like initial mass function and an assumed disk thickness of 250 pc the resulting supernova rate density is S ∼ 280 kpc⁻³ Myr⁻¹. For an average gas number density of n₀ = 1 cm⁻³ the expectation value would be only N_hot ∼ 6 × 10⁻⁴. Due to the strong power-law dependence on the density in Eqn. 10 a lower density of n = 0.015 cm⁻³ results in N_hot ≳ 1 and a stable volume filling hot phase can form. Once such a condition is reached and the system cannot vent the hot gas it will undergo a thermal runaway. Subsequent supernovae explode in even hotter and lower density regions with even less thermal losses and larger shell formation radii. Once the volume is dominated by over-pressured hot gas no shell will form, cooling losses are minimal and most of the mass is in small cold clumps. This process has recently been described by Gatto et al. (2015) and Li et al. (2015) with hydrodynamical simulations in periodic boxes. If the ISM can vent the hot gas, an outflow is driven.

The strong dependence of the hot gas volume filling fraction in Eqn. 10 on the environmental density of the supernova explosions has significant consequences for the evolution of the galactic ISM. In Fig. 6 we illustrate this with three numerical experiments (part of the SImulating the Life Cycle of molecular Clouds [SILCC] simulation project, Walch et al. 2015). The setup is a stratified galactic disk with a surface density of Σ_gas = 10 M_⊙ pc⁻² embedded in a stellar disk potential. The initially homogenous ISM is driven by supernova explosions at a constant rate based on observational estimates. If all supernovae explode at the current density peaks (typical densities of n = 100 cm⁻³, see Girichidis et al. 2016b) the explosions suffer from radiative losses, no hot phase develops and the impact is limited to momentum injection. Rapidly a turbulent, pressure supported two phase (warm and cold gas) medium develops and the scale height is set by the turbulent pressure. Draine (2011) presents a simple estimate for this process to take only 2 Myrs. This behavior is reported from pure momentum injection models (Ostriker & Shetty 2011, Kim, Kim & Ostriker 2011, Kim, Ostriker & Kim 2013, Kim & Ostriker 2015b). The major shortcomings of these models are that no hot phase can develop and the cold phase cannot become dense enough for molecular gas formation (see e.g. Walch et al. 2015). If some half of the supernovae do not explode in density peaks but rather at random locations in the disk, as would be expected from the number of early-type 'runaway' stars discussed below, the ambient density distribution for supernovae becomes bimodal. Random supernovae in low density regions n ∼ 0.1 cm⁻³ compress the cold gas to higher densities n ≳ 100 cm⁻³, where the peak supernovae explode. The system can form a hot phase (see middle panels of Fig. 6). Once all supernovae explode at random positions (most ambient densities n ≲ 0.1 cm⁻³) the ISM becomes highly structured and rapidly develops a stable hot phase, which is expanding into the halo and drives a galactic outflow (see Girichidis et al. 2016b for the models shown in Fig. 6). This behavior has already been reported by pioneering three-dimensional hydrodynamical simulations of stratified disks by Korpi et al. (1999), de Avillez (2000), de Avillez & Breitschwerdt (2004), and Joung & Mac Low (2006). The major shortcomings of these type of models are that they neglect the galactic environment (radial gas flows and inflows) and, due to the idealized gemoetry, gas flows into and out of galactic halos cannot be modelled accurately (see e.g. Martizzi et al. 2016).

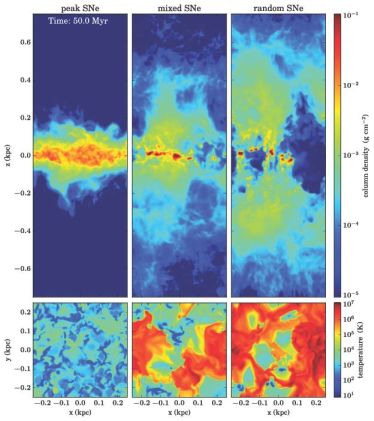Figure 6. Snapshots of the vertical gas column density distribution (top panels) and mid-plane temperatures (bottom panels) for three simulations of stratified galactic disk (Σgas = 10 M⊙ pc−2 shaped by supernovae (SNe) exploding at a constant rate (taken from the SILCC simulations, (Walch et al. 2015, Girichidis et al. 2016b). In peak SNe (left panels) each supernova explodes at the current density peak. Rapid thermal losses limit the SN impact to momentum ejection driving an (unrealistic) turbulent two-phase medium with no outflows and no hot gas. With 50 per cent of the supernovae exploding at random positions at lower densities a hot phase appears (mixed SNe, middle panel). If all SNe explode at random positions the hot phase becomes volume filling and drives a vertical outflow (random SNe, right panles, see Girichidis et al. 2016b). This figure clearly illustrates the strong impact of the actual location of SN explosions on the multi-phase structure of the ISM and the driving of outflows (see Eqn. 10). We note that non of these variations can be captured in current large scale cosmological simulations which have single resolution elements of the size of the above simulation boxes (∼ 500 pc) and rely on sub-resolution models.

OH maser measurements indicated that only about 15 per cent of core collapse supernovae interact with dense molecular gas (Hewitt, Yusef-Zadeh & Wardle 2009). Therefore the typical ambient density for explosions is lower than the dense birth places of massive stars. Now the questions is which astrophysical processes determine the ambient densities of supernova explosions? There are two phenomena which can result in this: the massive stars move away from their dense birth places into gas with lower volume densities and larger volume filling fractions and/or the stars change their environmental densities by stellar winds, ionising radiation and clustered supernova explosions.

Most, if not all, stars form in star clusters and are expected to be temporally and spatially correlated, eventually driving super-bubbles with more efficient energy coupling and momentum generation (e.g. Mac Low & McCray 1988, Joung & Mac Low 2006, Sharma et al. 2014). The typical velocity dispersion in newly born star clusters is ∼ 1 km s⁻¹ or 1 pc Myr⁻¹. Assuming the cluster becomes unbound massive stars can travel up to 40 pc before they explode (assuming typical supernova delay times for single stellar populations). These 'walkaway' stars can therefore easily leave their dense birthplaces and explode in lower density regions. As most of the volume of the ISM is not in the cold phase most supernovae might explode in the warm or hot phase, significantly changing the coupling efficiency (Slyz et al. 2005, Ceverino & Klypin 2009). There is also the 'runaway' star population (Gies & Bolton 1986) (about 45% of O-stars and 15% of B-stars are 'runaways') with typical velocities of ∼ 30 − 40 km s⁻¹ and maximum velocities as high as a few hundred km s⁻¹ (e.g. Silva & Napiwotzki 2011). These high-velocity stars originate from close binary systems becoming unbound by a supernova explosion (Zwicky 1957, Blaauw 1961) and/or from dynamical interactions in dense regions of star clusters (Poveda, Ruiz & Allen 1967). They can travel up to several hundreds of parsecs away from their birthplaces far into inter-arm regions or the lower galactic halo. Their explosion locations in galactic disks can therefore be considered as almost random, similar to the explosions of SNe Ia which contribute about 20 -25% to the supernova rate in the solar neighborhood (Tammann, Loeffler & Schroeder 1994). They explode independently of the gas mass distribution within the ISM, a process approximately taken into account in high-resolution simulations of stratified disks which are most useful to study the launching of outflows and, at the same time, create a realistically structured ISM (e.g. de Avillez & Breitschwerdt 2005, Joung & Mac Low 2006, Hill et al. 2012, Li, Bryan & Ostriker 2016). Such detailed small scale simulations with a realistic ISM structure will help to bridge the gap in scale and physical understanding to galaxy scale simulations.

3.2. Stellar winds

Massive stars themselves also impact their ambient medium. Radiation driven stellar winds from O- and B-stars (Castor, Abbott & Klein 1975, Puls et al. 1996, Kudritzki & Puls 2000) create bubbles of low density gas around the stars. Typical B-stars with masses ∼ 9 M_⊙, mass-loss rates of _wind ∼ 10⁻⁹ M_⊙ y⁻¹, and wind velocities of v_wind ∼ 2000 km s⁻¹ have an intergrated wind luminosity of only a few times ∼ 10⁴⁷ erg. However, very massive stars can reach as much as E_wind ∼ 10⁵¹ erg. Although energetically much less important than supernova explosions, stellar wind blown bubbles can significantly reduce the gas densities around massive stars and thereby increase the impact of the supernovae. Furthermore, since momentum injection goes as / v, winds from massive stars can contribute more direct momentum than the supernovae themselves. Interestingly, stellar winds can also significantly reduce the star formation process in forming star clusters (Dale & Bonnell 2008), although Dale et al. (2013, 2014) argue that the combined effect of stellar winds and ionising radiation only has modest impact on star formation) and might be a stronger regulator for galactic star formation than supernovae (Gatto et al. 2016).

3.3. Radiation

Stellar evolution models indicate that the total energy released by newly formed stellar populations is, by a large margin of two orders of magnitude, dominated by stellar radiation, which itself is dominated by massive stars (e.g. Leitherer et al. 1999). By the time the first supernova, with a canonical energy of 10⁵¹ erg, has exploded, the stars would have already emitted ∼ 10⁵³ erg as radiation, and ≳ 10⁵⁰ erg in stellar winds. It has been realized lately that, in galaxy scale simulations, accounting for the stellar luminosity (and winds) might significantly enhance the coupling of the stellar energy and momentum output to the ISM (e.g. Hopkins, Quataert & Murray 2011, Hopkins, Quataert & Murray 2012a, Agertz et al. 2013, Roškar et al. 2014). The generation of momentum is of particular interest as it cannot easily be radiated away like thermal energy. The efficient cooling results in only a moderate, 10%, contribution of the thermal energy density in the ISM (Boulares & Cox 1990). Due to the generally severe radiation losses in dense interstellar environments it is, however, unclear, how much of the injected energy can be converted into momentum. If this process is efficient, then stellar radiation might significantly contribute to the driving of turbulence and the launching of galactic winds (e.g. Murray, Quataert & Thompson 2005, 2010, Murray, Ménard & Thompson 2011, Geen et al. 2015, Agertz & Kravtsov 2015).

Ionizing UV photons create HII regions around young massive stars by heating the parental cloud from ≲ 100 K to ∼ 10⁴ K. At this stage the dynamics of the ISM is dominated by the thermal pressure of the ionized gas with sound speeds ≲ 10 km s⁻¹. The momentum input by direct absorption of UV photons (single scattering) seems sub-dominant (Mathews 1969, Spitzer 1978, Arthur et al. 2004, Krumholz & Matzner 2009, Sales et al. 2014). It might be sufficient to drive turbulence at a low level (Gritschneder et al. 2009) and even disrupt small clouds on short time-scales (Krumholz, Matzner & McKee 2006, Walch et al. 2012), however, over-dense regions of the surrounding ISM will also be compressed into clumps and pillars (Dale, Bonnell & Whitworth 2007, Gritschneder et al. 2010, Walch et al. 2012) making further coupling more difficult.

A full radiation transfer treatment of ionizing radiation from massive stars in galaxy scale simulations is technically challenging (see e.g. Wise et al. 2012 for single scattering). It has been approximated in a Strömgren approach, i.e. the ISM around massive stars corresponding to a Strömgren sphere (Strömgren 1939) is ionized and heated to ∼ 10⁴ K (e.g. Renaud et al. 2013, Hopkins, Quataert & Murray 2012a) or in the optically thin regime (assuming escape fractions from 'clouds') with radiation field attenuation to follow the impact on gas cooling (e.g. Kannan et al. 2014). Kannan et al. (2014) claim a significant impact of the local UV radiation resulting in a suppression of star formation for Milky Way like galaxies (∼ 40%) by increasing the cooling time and the equilibrium temperature.

It has been argued that the radiation pressure on dust of re-emitted and scattered infrared radiation can result in a significant momentum input into the ISM,

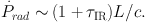(11)

The efficiency of this process depends on the optical depth to the re-radiated long-wavelength emission of the dust, τ_IR, i.e. on the details of multiple scatterings in optically thick regions surrounding the young stars. Based on small scale simulations, Krumholz & Thompson (2013) argue that the momentum input does not exceed L / c due to the structure, and therefore inefficient trapping, developing in the ISM (Krumholz & Thompson 2012). However, using a different radiation transport method, Davis et al. (2014) find a slightly stronger coupling of the radiation. In an attempt to approximately include this effect in high resolution galaxy scale simulations (Hopkins, Quataert & Murray 2011, 2012a, 2012b) add momentum to the surrounding gas either in a stochastic or continuous way and indicate that they can use this process to drive galaxy scale winds. Hopkins, Quataert & Murray (2011) give the gas particles initial kicks of the order the escape velocity from local 'gas clumps' or 'star clusters' (between 60 km s⁻¹ and ∼ 350 km s⁻¹ for 'clusters' with masses ∼ 10⁵ − 10⁹ M_⊙) guaranteeing that dense regions become unbound before additional radiation pressure and supernovae can act. Locally they approximately compute τ_IR from the local gas properties assuming a high dust opacity of ∼ 5 cm² g⁻1 (see also Roškar et al. 2014) and use a model for attenuated radiation to compute the momentum input from all stars at large distances (Hopkins, Quataert & Murray 2011). This empirical implementation of radiation pressure may result in large scale galactic winds by a non-linear interaction of the different feedback mechanisms with the wind mass-loading changing as a function of galaxy properties (Hopkins, Quataert & Murray 2012a).

Other groups have followed similar paths to account for the full energy input of stellar populations and approximate the effect of radiation pressure. Agertz et al. (2013) have implemented the local momentum input as in Eq. 11 with photon trapping acting at early (t ≲ 3 Myr) embedded stages. Aumer et al. (2013) assume a large, fixed, value for the optical depth (τ_IR ∼ 25) and scale the momentum input with the local gas velocity dispersion and metallicity. In a cosmological context it has been demonstrated, using different codes, that such efficient momentum input and the resulting winds can promote the formation of disk galaxies with appropriately low conversion efficiencies (Hopkins et al. 2014, Agertz & Kravtsov 2015, see Fig. 2). However, Roškar et al. (2014) implemented an approximate radiation transfer for ultraviolet and infrared radiation, where the dust opacity becomes an important factor to regulate the feedback efficiency. They argue that the momentum input required to drive strong outflows at the same time disturbs the gas and the resulting stellar disk so much that it becomes impossible to retain the flat disk morphology. In summary, while many promising calculations have been made (see e.g. Rosdahl et al. 2015 for a first application of radiative transfer processes in galaxy-scale simulations), it is not yet clear how much radiation from young stars can really contribute to the driving of strong galactic outflows. For a complete understanding of this process more accurate models for dust evolution in galaxy formation simulations have to be considered. Good steps forward have been recently made also in this direction (e.g. Bekki 2015, McKinnon, Torrey & Vogelsberger 2016, Zhukovska et al. 2016).

3.4. Magnetic fields and cosmic rays

Magnetic fields and cosmic rays (CRs), relativistic high-energy particles, mostly protons and electrons, are an integral, non-thermal component of the interstellar medium. In the solar neighborhood the energy density in CRs, magnetic fields and the kinetic energy density are comparable and significantly higher than the thermal pressure (Boulares & Cox 1990, Ferrière 2001). CR spectra have been measured over many orders of magnitude from E_CR ∼ 10⁷ eV up to the energies of E_CR ∼ 10²⁰ eV. As the galactic CR energy spectrum is rather steep with P ∝ E^−2.7 the majority of the energy is deposited at lower energies with a peak at around a few GeV, which is the expected range of significant dynamical impact of CRs on the ISM within a star forming galaxy. The main acceleration mechanism for galactic CRs, in particular those below the 'knee' in the CR spectrum is considered to be diffusive shock acceleration (DSA, see e.g. Bell 1978, Blandford & Ostriker 1978) and non-linear DSA (Malkov & O'C Drury 2001) in shocks of supernova remnants (SNR) (see Hillas 2005, for a review, and recent observations by Ackermann et al. 2013). Although both electrons and protons are accelerated in strong shocks, the protons carry most of the energy stored as cosmic rays.

The fraction of energy generated in supernova shocks is highly uncertain and this process can, of course, not be simulated in galaxy scale simulations. The estimates mostly range between 5 and 30% of the total supernova explosion energy (Kang & Jones 2006, Ellison et al. 2010) with increasingly fundmagental, ab initio calculations now being made (e.g. Caprioli, Pop & Spitkovsky 2015). If a significant fraction is 'stored' in cosmic rays - which cool much slower than thermal gas by hadronic interactions and Coulomb and ionization losses - they can be carried over large distances and significantly impact the ISM, provided the coupling between CRs and the thermal gas is strong enough (e.g. Breitschwerdt, McKenzie & Voelk 1991, Zweibel & Heiles 1997). CRs diffuse from the shocks and, later on, stream through the ISM. The bulk of CRs may be trapped at first by scattering at self-excited Alvén waves, which causes a slowed down outward diffusion and additional mometum transfer to the gas (Caprioli, Pop & Spitkovsky 2015). Once the cosmic rays are able to escape the supernova remnant, a streaming instability will be excited if the necessary conditions for the dynamical coupling between the CRs and the gas are met (i.e. a large-scale CR gradient towards the galactic halo is required, Kulsrud & Pearce 1969), effectively transferring CR energy and momentum to the thermal gas. In addition the CRs exert a pressure on the thermal gas by scattering off Alfvén waves. It is therefore expected that CRs have a significant impact on the thermal and dynamical properties of the ISM. The propagation of cosmic rays through the ISM is complex and often approximated by diffusion with coefficients of the order κ_CR ∝ 10²⁸ − 10²⁹ cm s⁻¹ (e.g. Strong & Moskalenko 1998, Trotta et al. 2011, Tabatabaei et al. 2013). Locally the diffusion might be anisotropic with significantly smaller coefficients perpendicular to the magnetic field lines. On global galactic scales of the Milky Way, however, the diffusion can be considered isotropic (Strong, Moskalenko & Ptuskin 2007). The lifetime of the several GeV cosmic ray fluid is known from radioactive dating to be roughly 10 million years.

In addition to thermal and radiation pressure caused by stellar feedback, CRs turn out to be an important agent on galactic scales and, once accelerated in regions of local feedback from star formation, they might be efficient in supporting or even driving galactic outflows. Already in the beginning of the 90's it has been proposed that the combined effect of thermal pressure, MHD waves, and an effective (non-thermal) CR pressure (McKenzie & Voelk 1982) is able to drive a galactic wind (Breitschwerdt, McKenzie & Voelk 1991, Breitschwerdt, McKenzie & Voelk 1993), even if the star formation rate is moderate. Recent observations of the starburst galaxy M82 (VERITAS Collaboration et al. 2009) reveal CR densities which are 500 times higher than in the Milky Way and thus clearly link the CR density with regions of highly efficient star formation. Other groups have argued that the galactic wind in M82 is purely driven by strong stellar feedback (Chevalier & Clegg 1985, Völk, Aharonian & Breitschwerdt 1996). However, in normal spirals like the Milky Way, stellar feedback is probably not strong enough to drive a large-scale galactic wind. Nevertheless, recent ROSAT observations of the Milky Way show extended, soft X-ray emission, which is best explained with a kpc-scale wind for which the cosmic ray pressure may be essential (Everett et al. 2008).

In galaxy scale hydrodynamics simulations with SPH and AMR codes, cosmic rays have recently been included as a separate fluid, as their mean free path is shorter than the typical length scales resolved (Skilling 1975). The fluid is treated as a relativistic gas with γ_cr = 4/3 and is advected with the gas. The resulting total pressure is p_tot = p_th + p_cr with p_cr = (γ_cr − 1) E_cr. In addition the cosmic rays are allowed to diffuse through the ISM. This is treated approximately either by streaming (Uhlig et al. 2012) or by isotropic diffusion with a typical diffusion coefficient (Enßlin et al. 2007, Jubelgas et al. 2008, Booth et al. 2013, Salem & Bryan 2014). In simulations following magnetic fields the diffusion is treated anisotropically with one or two orders of magnitude lower diffusion coefficients along the magnetic field lines (Yang et al. 2012, Hanasz et al. 2013, Pakmor et al. 2016).

All simulations including cosmic rays on galactic scales indicate that they can significantly support the driving of bipolar galactic winds with velocities exceeding the local escape speed and with mass loading greater than unity. The winds are driven by the additional pressure gradient due to cosmic rays in low density regions (Uhlig et al. 2012, Hanasz et al. 2013, Booth et al. 2013, Salem & Bryan 2014, Pakmor et al. 2016, Salem, Bryan & Corlies 2016). This process is only efficient if cosmic rays can diffuse out of the high density regions, where they are dynamically unimportant, to build-up a galaxy wide vertical gradient (see e.g. Uhlig et al. 2012, Booth et al. 2013). The mass loading of cosmic ray driven winds is higher for lower mass galaxies (Wadepuhl & Springel 2011, Uhlig et al. 2012, Booth et al. 2013) but also for gas rich massive galaxies the effect is significant (Hanasz et al. 2013). Cosmic ray driven outflows can also support stable configurations of open magnetic field lines originating from regions of high star formation rates (Hanasz et al. 2013). These simulations might also be able to explain the detection of strong magnetic fields at large radii (∼ 50 kpc) around star forming galaxies at intermediate and high redshift (Bernet, Miniati & Lilly 2013).

Recently, simulations of the impact of cosmics rays on the interstellar medium on smaller scales have confirmed the ideas brought forward by larger scale galaxy formation simulations and analytic estimates. It was shown by Girichidis et al. (2016a), using magneto-hydrodynamic simulations with anisotropic diffusion that cosmic rays indeed support the launching of outflows from galactic disks and the basic results seems to be insensitive of the magneto-hydrodynamical method used, details of the star formation algorithm and the presence of self-gravity (Simpson et al. 2016). It remains to be seen whether the supporting role of cosmic rays (i.e. the pressure gradient) for the driving of outflows is significant or whether the computations still suffer from inaccuracies in capturing the accurate effect of supernova explosions on the formation of a hot, wind driving, gas phase.

The simulations presented above can only be the starting point for more detailed investigations of the potential importance of cosmic rays for the driving of galactic outflows. In galaxy scale simulations, the galactic ISM is in general unresolved, with a significantly simplified treatment of energy injection by SNe as well as cosmic ray transport. Also the global and local evolution of the galactic magnetic field has to be considered and significant progress has been made recently (Dolag et al. 2005, Dolag, Bykov & Diaferio 2008, Dolag & Stasyszyn 2009, Kotarba et al. 2009, 2010, Dubois & Teyssier 2010, Pakmor & Springel 2013, Pakmor, Marinacci & Springel 2014, Pakmor et al. 2016, Rieder & Teyssier 2016). If it turns out that CRs and magnetic fields are indeed as important as suggested they have the potential to become a 'global player', regulating the evolution of the ISM and the efficiency of galaxy formation across cosmic times.

3.5. Mechanical and radiative AGN feedback

While the significant work done by many groups using 'thermal AGN feedback' (see Section 2.3) has solid motivation and has produced many quite useful results, the somewhat arbitrary physical implementation has troubling aspects that several groups have attempted to remedy. First, there is no physical means specified for communicating the energy from the black holes to the surrounding gas in these treatments (see discussion in Ostriker et al. 2010). In actual AGN systems, there are high velocity winds and radiation output for both of which there is a momentum associated with the energy transfer and there is a spatial direction for the momentum outflow (Churazov et al. 2005, Merloni & Heinz 2008, Fabian 2012). But in a purely thermal feedback approach these physical factors are missing and, more importantly, the mass to which the thermal feedback energy is distributed is not specified or defined by a heating threshold (Section 2.3). Adding this energy to a very small mass would produce very high temperatures and radiative energy losses, adding it to a very large mass would produce small additional velocities compared to the virial velocities in the galaxy, so adding to the 'just right' amount of mass seems to be required. But if teh added feedback energy is deposited with the appropriate accompaning momentum, as observed in BAL winds, the energy redistribution is achieved by physical means.

There exists a characteristic electromagnetic spectrum for AGN with peaks in the infrared, ultraviolet and X-ray (e.g. Sazonov, Ostriker & Sunyaev 2004) that can be taken as the emitted output with the ratio of electromagnetic output to mass accretion given by the Soltan argument (Soltan 1982). In addition to relativistic jets there are also broad-line winds observed to be commonly emitted by AGN (Yuan & Narayan 2014) and these too have been calibrated to the accretion rate empirically (Arav et al. 2013, see also Krolik 1999). Thus one can specify the output in mass, energy, momentum and radiation in various bands per mass accreted on the basis of approximate matches to observed AGN, and then the thermal, mechanical and radiative coupling of these components to the surrounding medium should be handled automatically by the hydro codes being utilized. When taking this approach (and including the Eddington force rather than putting in a limit) the accretion rate self-adjusts, so no arbitrary multiplicative 'boost' factors may be needed in implementing the Bondi-Lyttleton accretion. First attempts to approximately include the effects of UV and X-ray emission from accreting black holes have been made (e.g. Hambrick et al. 2011, Choi et al. 2015, Vogelsberger et al. 2013, Roos et al. 2015, Bieri et al. 2016). Both mechanical (BAL) and radiative effects are included in Choi et al. (2016) for cosmological simulartions and in Hopkins et al. (2016) for high-resolution simulations of galactic centers. However, in the end, the results of this more complex approach are in fact similar to those of the thermal feedback approach with regard to regulating the overall mass growth of the central black hole, but other aspects are very different. For example, the fluctuation level of the kinetic feedback is far more extreme with 'on' periods rarely exceeding several million years and a small overall duty cycle being expected. And, as noted earlier, correct prediction of the thermal X-ray emssion from massive galaxies provides a strong test of the feedback mechanism which indicates that including a kinetic wind component is essential (Choi et al. 2015, Weinberger et al. 2016).

Jets from AGN are frequently observed and feedback from this mechanism is sometimes called 'radio mode' (Fabian 2012, Heckman & Best 2014). Some cosmological galaxy evolution treatments have included this process (e.g. Dubois et al. 2014), the reality of which is not in doubt. But narrow relativistic jets effectively drill through the ISM within galaxies, leaving a dramatic imprint on the surrounding cluster gas but probably not communicating significant amounts of energy or momentum to the ISM of the parent galaxy (Vernaleo & Reynolds 2006). However, potential coupling mechanisms e.g. turbulent mixing and dissipation exist and are studied in detail with higher resolution simulations (Omma et al. 2004, Scannapieco & Brüggen 2008, Gaspari, Brighenti & Temi 2012, Babul, Sharma & Reynolds 2013, Li & Bryan 2014). Jets being extremely important in regulating cooling flows within clusters are probably less important than other, more prosaic processes in determining the internal evolution of galaxies.