Galaxies form by a succession of mergers of cold dark matter halos,
the baryons dissipating and forming a dense core. Isolated infall
plausibly
results in disk formation. Disk merging concentrates the gas into a
dense spheroid. The transition from linear theory to
formation of self-gravitating clouds occurs at an overdensity of about
crit
200. A simple ansatz
due to Press and Schechter yields the mass function of newly nonlinear objects
where
where
n
To match the observed luminosity function and predicted mass function
requires specification both of
However it is the detailed measurement of M/L that leads to a
possible problem.
One has to normalise M/L by specifying the mass-to-light ratio of
luminous galaxies.
The observed luminosity function can be written as
where
where vc is the disk circular velocity.
Dwarfs are preferentially disrupted by winds. In this way one can fit
Potential difficulties arise as follows. Simulations of mass loss from
dwarf galaxies suggest that supernova ejecta may contribute to
the wind but leave much of the interstellar gas bound to the galaxies.
34 This
would be a serious problem as one relies on redistribution of the
baryonic reservoir to form massive galaxies. Another problem arises
with the Tully-Fisher relation. This is the measured relation,
approximately L
where µL is the surface brightness of the
galaxy. Since µL
has a narrow dispersion for most disk galaxies, the Tully-Fisher
relation, where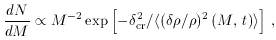
2
<(
/ )2 (M,t)> is
the variance in the density fluctuations. The variance at 8
h-1 Mpc,
8, is given by
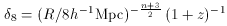
-1 on cluster scales but
n -2 on galaxy scales,
and M = 1015 
h-1 (R / 8h-1 Mpc)3
M
.
Of course the luminosity function rather than the mass function is
actually observed. We define 
/
g, where
g is the variance in
the galaxy counts. On cluster scales,
one finds that _8
0.6 (± 0.1) yields
the observed density of clusters if
= 1. More generally,
8 scales
as -0.6. A larger
is required for a given number
density of objects in order to account for the reduced growth in
as
is decreased below unity.
8 and of the mass-to-light
ratio. Much of the dark mass is in objects that were the first to go
nonlinear, as well as in the objects presently going nonlinear. Hence
one crudely expects that M/L
400 h,
as measured in rich clusters. The global value of M/L is
M/L
1500 h, and happens to
coincide with the mass-to-luminosity ratio measured for rich clusters if
0.4. This suggests that
these clusters may provide a fair sample of the universe. Even if most
dwarfs do not survive, because of subsequent merging, the relic dwarfs are
expected to have high M/L. Later generations of galaxies should have
undergone segregation of baryons, because of dissipation, and the
resulting M/L is reduced. Many of the first dwarfs are disrupted to
form the halos of massive galaxies. The predicted high M/L (of order
100) is consistent with observations, both of galaxy halos and of the
lowest mass dwarfs (to within a factor of ~ 2).
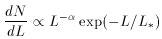
1 - 1.5,
depending on the selection criterion, and
L*
1010 h-2
L. Matching to the predicted
mass function specifies M/L for L* galaxies, as
well as the slope
of the luminosity function. One forces a fit to
by invoking
star formation-induced feedback and baryonic loss. This
preferentially reduces the number of low mass galaxies. A typical
prescription is
33 that
the retained baryonic fraction is given by
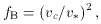
. There is no longer any
freedom in the luminous galaxy parameters.
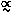V
rot, between galaxy
luminosity and maximum rotational velocity. In effect, the
Tully-Fisher relation offers the prescription
for M/L within the luminous part of the
galaxy, since the virial theorem requires
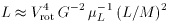
3 is measured in the
I band and
4
is appropriate to the near infrared, effectively constrains M/L. The
normalization of the Tully-Fisher relation requires M/L
5h
for early-type spirals, as is observed directly from their rotation
curves within their half-light radii. However simulations of
hierarchical clustering, which incorporate baryonic cooling and star
formation with a prescription designed to reproduce the luminosity
function, give too high a normalization for M/L in the predicted
Tully-Fisher relation: at a given luminosity the rotational velocity
is too high.
35
Moreover the efficient early star formation required in
order to fit the luminosity function requires the Tully-Fisher
normalisation to change with redshift: galaxies are
predicted to be brighter by about
a magnitude at a given rotation velocity at z ~ 1,
and this exceeds the observed offset.
36
Resolution of
the Tully-Fisher normalization remains controversial.