


2.1. The equations of statistical equilibrium
In order to calculate the level populations of a given atom or ion, we make two basic assumptions :
To calculate the population of some level i, we must take into account all possible processes that will (de)populate it:
where ni is the volume density of atoms or ions in
level i.
Therefore, in steady state regime the sum over all processes that
populate level i will
be balanced by the sum over all processes that depopulate level
i. Assuming that the two
conditions listed above are met, this can be written
(see, for instance, Rybicki and Lightman
[3]):
where we have considered all possible bound-bound processes, i.e.,
spontaneous,
radiation-induced and collisionally-induced.
The lefthand side of eq. (2) is the sum over all processes that populate
level i
from the other levels j, whereas the righthand side is the sum
over all processes that depopulate level i to levels j.
Aij is the transition probability of spontaneous decay
from level i to level j. For
i
Bij are Einstein coefficients, related to the
transition probabilities by:
for i > j, and Bii = 0; h is
Plank's constant, Ei is the energy of level
i (expressed in cm-1) and gi is the
statistical weight of level i.
uij is the spectral energy density of the radiation
field integrated along the line profile
with uii = 0;
In eq. (2) we have also considered the effect of collisions;
nk is the volume
density of the particle inducing the transition, the main collision
partners usually being
k = e-, p+,
H0, He0, H2,... ,
depending whether the medium is primarily ionized or neutral.
qkij is the collision rate for the
transition from level i to level j induced by
the collision partner k .
These coefficients are the cross-sections for the related process
for the deexcitation rates (i > j); k is
Boltzmann's constant, T is the kinetic temperature,
µ is the reduced mass of the system and
Excitation and deexcitation rates are related by the principle of
detailed balance:
with qii = 0.
When the interaction is coulombian, as in collisions with electrons, it
is convenient
to express the cross-section in terms of the collision stregth
where m is the electron's mass. Substituting this in eq. (5) yields:
with T expressed in K and
These are the basic parameters needed to solve eq. (2). If we consider
our model ion
to be composed of n levels, then we must solve a linear system of
n - 1 equations in order to calculate the relative population ratios.
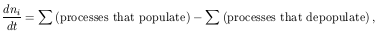
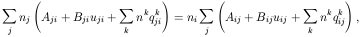
 j,
Aij = 0.
j,
Aij = 0.
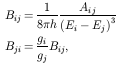

 of the transition from level i to level j:
of the transition from level i to level j:
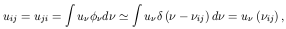
 ij is the frequency of the
transition and we have assumed that the radiation field
does not vary significantly along the line profile.
ij is the frequency of the
transition and we have assumed that the radiation field
does not vary significantly along the line profile.
 ij
convolved with a Maxwellian distribution of velocities
f(v), making
these quantities suitable for astrophysical applications
(see, for instance, Osterbrock
[4]):
ij
convolved with a Maxwellian distribution of velocities
f(v), making
these quantities suitable for astrophysical applications
(see, for instance, Osterbrock
[4]):
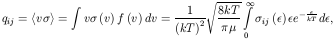
 is the collision partner's
kinetic energy.
is the collision partner's
kinetic energy.
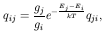
 ij,
defined by:
ij,
defined by:
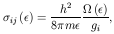
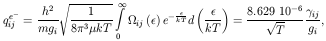
 ij is
defined by the integral in eq. (8)
and is called Maxwellian-averaged collision stregth. Typically
ij is
defined by the integral in eq. (8)
and is called Maxwellian-averaged collision stregth. Typically
 ij is a slowly
varying function of T, of order unity. However, for neutral atoms it may
vary for several orders of magnitude.
ij is a slowly
varying function of T, of order unity. However, for neutral atoms it may
vary for several orders of magnitude.