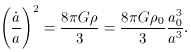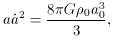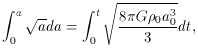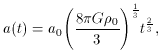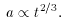1. The Einstein-DeSitter Model
The Einstein-DeSitter model is a matter dominated Friedmann model with zero curvature (k = 0). This model corresponds to a Minkowski universe (zero curvature), in which the universe will continue to expand forever with just the right amount of energy to escape to infinity. It is analogous to launching a rocket. If the rocket is given insufficient energy, it will be pulled back by the Earth. However, if its energy exceeds a certain critical velocity (escape velocity), it will continue into space with ever increasing speed. If it has exactly the escape velocity, it will proceed to escape the Earth with a velocity going to zero as the rocket approaches spatial infinity. The Einstein-DeSitter model corresponds to the universe having exactly the right escape velocity provided by the Big-Bang to escape the pull of gravity due to the matter in the universe.
By substituting k = 0 into (29) and (28), the Friedmann equations become
By solving (31) for
If the density of the universe exceeds the critical density, the
universe is open. Conversely, if the density is below
This is equivalent to roughly 10 hydrogen atoms per cubic meter.
Although, this is incredibly small compared to Earthly standards,
it must be remembered that most of space is empty and the concern
is the total energy density.
Notice that the critical density depends on the Hubble constant.
This means that the density required for a flat universe will
change with time, in general, as the universe expands. For the
universe to be `fine-tuned' to this precision is highly
improbable; yet, most observations suggest this type of geometry.
This paradoxical issue is referred to as the Flatness problem and
will lead to one of the claimed triumphs of Inflation theory.
Because it is believed that the universe is so close to being
flat, it is useful to define the density parameter,
The quantity
From the previous result for a matter dominated energy density, we
found
This can be used to obtain a useful
relation for
Returning to the Friedmann equation (31) and
substituting the above expression for
Combining terms in a,
now integrating,
So for the Einstein-DeSitter Model, the scale factor evolves as
t2/3.
,
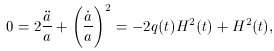
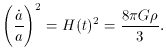
a critical
density can be found for a flat universe. The critical density is
the amount of matter required for the universe to be exactly flat
(k = 0) and is a function of time. The critical density at the
present is defined as,
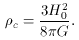
c the
universe is open. For the observed Hubble parameter as
defined in (2), the critical density today
corresponds to a value,
.
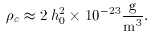
0 is the ratio of
the density observed today,
0, to the
critical density,
c. In general,
is the ratio of the density to
the critical value.
together with
Equation (30),
which implies q0 = 1/2, can be used to discriminate
between the possible geometries for the matter dominated universe
(see Table 2).
Geometry
q0 Fate of Universe Name
Flat =1 1/2 Open Universe Einstein-DeSitter Model
Hyperbolic <1 <1/2 Open Universe Open Model
Spherical >1 >1/2 Closed Universe Closed
~
a-3. From this relation, conservation of energy follows,
,
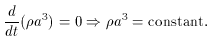
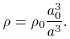
one finds,
