


One of the successes of the hot Big Bang model is its prediction of the light elements. These predictions are verified by observations of the structure and composition of the oldest stars, quasars, and other quasi-stellar remnants (e.g., QSOs) [18, 19, 20, 21]. The process by which the elements form is referred to as nucleosynthesis.
The Hot Big-Bang model predicts a universe that will go through several stages of thermal evolution. As the universe expands adiabatically, the temperature cools, scaling as
Here
and
Setting the Boltzman constant to unity,
This can also be understood using the
DeBroglie wavelength of the photon (for radiation)
[23].
The wavelength is inversely proportional to the
energy in natural units. This raises the issue of a possible
factor of redshifting for the DeBroglie wavelength of a massive
particle. For a particle the simple relation E = pc does not
hold; thus, the velocity of the particle can decrease to preserve
its wavelength. This redshifting is analogous to that of equation
(3) in the first section and gives an
alternative explanation of particles in motion settling into the
cosmic rest frame. This also explains why one might expect to
find primarily non-relativistic (cold) matter, which just means
particles traveling at speeds much less than c.
From relation (41) for the temperature, one has a
quantitative way to find critical temperature scales in the
evolution of the universe. For a given value of the curvature the
relation between the scale factor and time can yield an expression
between temperature and time. For example, in a matter dominated,
flat universe,
which was derived earlier.
In thermal physics one is usually interested in thermal
equilibrium. This consideration is accounted for by the condition,
This relations shows that the reaction
rate,
where
From equation (41), one can see that the universe began as
a point of infinite temperature and zero size. This is a singular
point for the history of the universe and the standard Big Bang
model (General Relativity) breaks down at this
singularity (15)
However, after the Planck time
(10-43) s one can follow the evolution using the concepts of
thermal physics and particle theory
(16)
In the earliest times following the Planck epoch, all matter
existed as free quarks and leptons. The existence of free quarks
(known as asymptotic freedom) is made possible by the high energy
(temperature) during the early moments of the Big Bang. The
universe cools, as indicated by (41), and the quarks
begin to combine under the action of the strong force to form
nucleons. This phase of formation is referred to as Baryogenesis,
because the baryons (e.g., protons and neutrons) are created for
the first time. The expansion continues to allow leptons, such as
electrons, to interact with nucleons to form atoms. At this
point, referred to as recombination, the photons in the universe
are free to travel with virtually no interactions. For example,
hydrogen is the most abundant element to form in nucleosynthesis
and at the time of decoupling the temperature of the photons has
dropped to around 3000 K. This corresponds to less than
13.6 eV, the energy needed to ionize the atoms.
Therefore, there are no longer free electrons to interact with the
photons and in fact the energy of a photon (around .26
eV, at this temperature) is so low that it can not
interact with the atoms. In this way the photons have effectively
decoupled from matter and travel through the universe as the
cosmic background discussed in Part II. A brief summary of the
most significant events are encapsulated below,
14 For the reader interested in learning
more about particle interactions see,
[9], Chapter 7],
[22, Chapter 9].
Back.
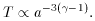
 is the ratio
of specific heats
and is equal to 4/3 for a radiation dominated universe
[22].
This relation is manifest, since the temperature
is equivalent to the energy density divided by the volume (in
natural units
is the ratio
of specific heats
and is equal to 4/3 for a radiation dominated universe
[22].
This relation is manifest, since the temperature
is equivalent to the energy density divided by the volume (in
natural units  = c =
k = 1). Moreover, the radiation energy
density is redshifted by an additional factor of 1/a(t) since
the Hubble expansion stretches the wavelength, which is inversely
proportional to the energy:
= c =
k = 1). Moreover, the radiation energy
density is redshifted by an additional factor of 1/a(t) since
the Hubble expansion stretches the wavelength, which is inversely
proportional to the energy:
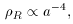
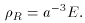
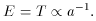
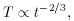
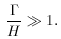
 , must be
much greater than the rate at which the
universe expands for thermal equilibrium to be reached.
, must be
much greater than the rate at which the
universe expands for thermal equilibrium to be reached.
 is related to the cross-section of the given particle interaction by
is related to the cross-section of the given particle interaction by
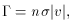
 is the cross-section,
|v| is the relative speed, and n is the number density of the
species (14)
is the cross-section,
|v| is the relative speed, and n is the number density of the
species (14)
15 Supersting Theory offers solutions to the
problem of a singularity by setting an ultimate smallness, the
Planck length (10-33 cm). This is outside the scope of this
paper, but the reader is referred to
[24] for an
excellent popular account of strings and cosmology and in
[25]
there are a number of papers with rigorous
treatments of string cosmology. Back.
16 For an introductory
survey of particle theory see
[26,
27] and for
particle physics in cosmology
[28] is an
excellent book.
The remainder of this paper will assume a basic knowledge of
particle theory and thermal physics. Back.