


The idea of quintessence
(4)
is that the
cosmological constant is small because the universe is old. One imagines a
uniform scalar field  (t)
that rolls down a potential
V(
(t)
that rolls down a potential
V( ), at a rate governed by
the field equation
), at a rate governed by
the field equation
where H is the expansion rate
Here
while
with pM the pressure of matter and radiation.
If there is some
value of
Recently this approach has been studied in the context of so-called `tracker'
solutions. (5)
The simplest case arises for a potential of the form
where
The nice thing about these tracker solutions is that the
existence of a cross-over from an early
Theories of quintessence offer no explanation why this should be the case.
(An interesting suggestion has been made after Dark Matter
2000. (6))
4 P. J. E. Peebles and B. Ratra:
Astrophys. J. 325, L17 (1988);
5 I. Zlatev, L. Wang, and
P. J. Steinhardt:
Phys. Rev. Lett. 82,
896 (1999);
6 C. Armendariz-Picon, V. Mukhanov, and
P. J. Steinhardt: astro-ph/0004134.
Back.
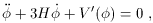
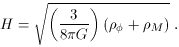

 is the energy density of the
scalar field
is the energy density of the
scalar field
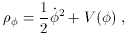
 M
is the energy density of matter and radiation, which decreases as
M
is the energy density of matter and radiation, which decreases as
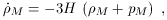
 (typically,
(typically,
 infinite) where
V'(
infinite) where
V'( ) = 0, then it is
natural that
) = 0, then it is
natural that  should approach this
value, so that it eventually changes only slowly with time. Meanwhile
should approach this
value, so that it eventually changes only slowly with time. Meanwhile
 M is
steadily decreasing, so that
eventually the universe starts an exponential expansion with a slowly varying
expansion rate H
M is
steadily decreasing, so that
eventually the universe starts an exponential expansion with a slowly varying
expansion rate H  sqrt[8
sqrt[8  G
V(
G
V( ) / 3]. The problem, of
course, is to
explain why V(
) / 3]. The problem, of
course, is to
explain why V( ) is small or
zero at the value of
) is small or
zero at the value of  where
V'(
where
V'( ) = 0.
) = 0.
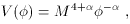
 > 0, and M is an
adjustable constant. If the scalar field begins
at a value much less than the Planck mass and with
V(
> 0, and M is an
adjustable constant. If the scalar field begins
at a value much less than the Planck mass and with
V( ) and
) and
 2 much less than
2 much less than
 M, then the field
M, then the field
 (t) initially increases as
t2/(2+
(t) initially increases as
t2/(2+ ), so
that
), so
that 
 decreases as
t-2
decreases as
t-2 /(2+
/(2+ ),
while
),
while  M is
decreasing faster, as t-2. (The existence of this phase
is important, because the success of cosmic nucleosynthesis calculations would
be lost if the cosmic energy density were not dominated by
M is
decreasing faster, as t-2. (The existence of this phase
is important, because the success of cosmic nucleosynthesis calculations would
be lost if the cosmic energy density were not dominated by
 M at
temperatures of order 109 °K to 1010
°K.) Eventually a time is reached when
M at
temperatures of order 109 °K to 1010
°K.) Eventually a time is reached when
 M becomes
as small as
M becomes
as small as 
 , after which the
character of the solution changes. Now
, after which the
character of the solution changes. Now

 becomes larger than
becomes larger than
 M, and
M, and

 decreases more slowly, as
t-2/(4+
decreases more slowly, as
t-2/(4+ ). The
expansion rate H now goes
as H
). The
expansion rate H now goes
as H  sqrt[V(
sqrt[V( )]
)]
 t-
t- /(4+
/(4+ ), so the
Robertson-Walker scale factor R(t) grows almost exponentially,
with log R(t)
), so the
Robertson-Walker scale factor R(t) grows almost exponentially,
with log R(t)
 t4/(4+
t4/(4+ ). In
this approach, the transition from
). In
this approach, the transition from
 M-dominance to
M-dominance to 
 -dominance is supposed to take place near the
present time, so that both
-dominance is supposed to take place near the
present time, so that both
 M and
M and

 are now both contributing
appreciably to the cosmic expansion rate.
are now both contributing
appreciably to the cosmic expansion rate.
 M-dominated expansion to a later
M-dominated expansion to a later

 -dominated expansion does not
depend on any fine-tuning of the
initial conditions. But it should not be thought that either of the two
cosmological constant problems are solved in this way. Obviously, the decrease
of
-dominated expansion does not
depend on any fine-tuning of the
initial conditions. But it should not be thought that either of the two
cosmological constant problems are solved in this way. Obviously, the decrease
of 
 at late times would be spoiled if
we added a constant of order
mPlanck4 (or
mW4, or me4)
to the potential (5). What is
perhaps less clear is that, even if we take the potential in the form (5)
without any such added constant, we still need a fine-tuning to make the value
of
at late times would be spoiled if
we added a constant of order
mPlanck4 (or
mW4, or me4)
to the potential (5). What is
perhaps less clear is that, even if we take the potential in the form (5)
without any such added constant, we still need a fine-tuning to make the value
of 
 at which
at which



 M close to
the present
critical density
M close to
the present
critical density
 c0. The
value of the field
c0. The
value of the field  (t) at
this crossover can easily be seen to be of the order of the Planck mass, so
in order
for
(t) at
this crossover can easily be seen to be of the order of the Planck mass, so
in order
for 
 to be comparable to
to be comparable to
 M at the
present time we need
M at the
present time we need
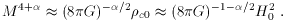
B. Ratra and P. J. E. Peebles:
Phys. Rev. D 37, 3406 (1988);
C. Wetterich: Nucl. Phys. B302, 668 (1988).
Back.
Phys. Rev. D 59, 123504 (1999).
Back.