3.3 Is the Fundamental Correlation with Local or Global Conditions?

The determination of the "dynamical center" of a cluster is problematic, especially for very irregular clusters. Because of this, Dressler used the local projected galaxy density (area encompassing the nearest ten galaxies) rather than the distance from the center of the cluster as his independent parameter when examining how the morphology of galaxies varied within a cluster. The use of local density resulted in excellent correlations, and led to the general interpretation that the subclusters are real physical associations and not chance projections, and some local mechanism determined the morphology of galaxies in clusters. In this section we shall reexamine this question by determining whether the morphology correlates better versus local galaxy density or R_cluster, the distance from the center of the cluster.

One difficulty is that the local galaxy density is a rather smooth function of the radius in regular clusters, making it difficult to determine which is the fundamental correlation. As a test, Dressler therefore uses both R_cluster and local galaxy density as the independent variable for six moderately irregular clusters. The correlation with local galaxy density appears to be better (see Dressler's Figure 5), leading him to conclude that populations are largely a function of local rather than global conditions.

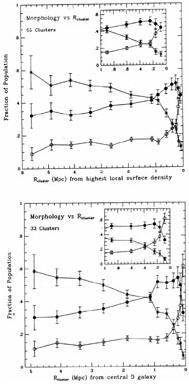
Whitmore and Gilmore (1990; hereafter WG) have reexamined Dressler's data in order to address this question. Figure 2a shows a comparison using first R_cluster as the independent parameter. It differs from Dressler's comparison in three respects: 1) it includes all 55 clusters, 2) the center is taken to be the galaxy with the highest local galaxy density rather than the centroid (which can often be in a relatively low density location), 3) the inner bin has been broken into six separate bins. We find that unlike Dressler's earlier results, the total range in the various populations is about the same when R_cluster is used as when local density is used, so it is not possible to determine which is the more fundamental parameter from Figure 2a. For example, the elliptical fraction ranges from about 10% in the outer low density regions to about 40% in both the inner regions and the highest density regions. One interesting new result is how sharply peaked the distribution of ellipticals is. Only within 0.5 Mpc of the center does the fraction rise dramatically. Using the local density as the independent parameter tends to obscure this point since the centers of open clusters may have relatively low local densities, and thus appear in the middle of the diagram in Figure 1. If the sample is restricted to the six moderately irregular clusters Dressler used in his Figure 5, the results are essentially the same, with the elliptical fraction going up to about 50% when either R_cluster or local density are used.

Figures 2a and 2b. a) The fraction of E (open circles), S0 (filled circles), and S+I (asterisks) galaxies as a function of the distance from the center of the cluster, Rcluster, using the same sample as Figure 1. The upper insert shows a blow up of the central 1 Mpc. b) Same as 2a but only including the 33 clusters containing D galaxies. (from WG)

Beers and Tonry (1986) have shown that the true dynamical center of a cluster is better defined by the location of a D or cD galaxy in the cluster, or the location of the peak of the X-ray emission, rather than on the basis of galaxy positions alone. If we restrict ourselves to the 33 clusters in Dressler's sample with D galaxies, the fraction of ellipticals goes up to 61% in the central bin (Figure 2b). This suggests that the elliptical fraction may be controlled by global properties, since D and cD galaxies tend to be found in the richer, more centrally-concentrated, X-ray emitting clusters.

The fact that the binning can have such an important role in determining the range in the morphological fractions led WG to divide the sample into 10 equal bins, arranged first by R_cluster and then local density. In both cases the maximum elliptical fraction reaches about 35%, making it impossible from this test to determine which parameter is more fundamental. The success of the morphology-density relation may simply reflect the fact that the local galaxy density is generally very well correlated with the position in the cluster.

Another interesting result is the apparent decrease in the fraction of S0 galaxies very near the centers of clusters. If this is not the result of some systematic classification problem it may indicate that the strong tidal shear has been able to destroy the disks of the S0 galaxies very near the cluster centers.

R_cluster may not be the optimal choice as the independent parameter. For example, the center of the Coma cluster is treated the same as the center of a very poor cluster when using R_cluster, even though the environmental affects are likely to be very different. WG have examined several other global parameters (e.g., local projected binding energy at each point in the cluster), and find that while several parameters result in as wide a range in the percentage of the ellipticals as when using local galaxy density is used, none are clearly better.

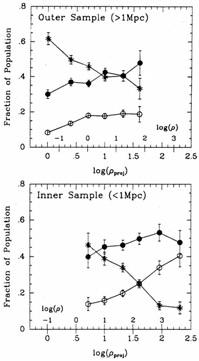
WG then break the sample into two groups, an inner sample including all galaxies within 1 Mpc of the cluster center, and an outer sample for galaxies beyond this radius. Figures 3a and 3b show the normal morphology-density relation for these two regions. The elliptical fraction shows almost no tendency to increase as a function of local density for the outer sample, while the elliptical fraction for the inner sample increases in a smooth progression. An estimate of the space density is also included, showing that this difference occurs for galaxies at similar space densities as well as similar projected galaxy densities. This figure suggests that the environment near the center of a cluster is needed to produce a high percentage of ellipticals.

Figures 3a and 3b. The morphology-density relation for the outer sample (only galaxies farther than 1 Mpc from the center). b) The morphology-density relation for the inner sample (only galaxies within 1 Mpc of the center). Both the local projected galaxy density and an estimated space density are included. (from WG). Same symbols as Figure 2.

The clearest difference is seen in the elliptical galaxies, although the spiral fraction may also be slightly steeper for the inner sample. The S0 fraction looks about the same in both samples. Sanromà and Salvador-Solé (1990) have performed a very clever test that implies that the morphology-density relation is driven by global effects for all three galaxy types, not just the ellipticals. Using Dressler's data, they produced artificial clusters by taking each galaxy and randomly repositioning them in angular coordinates around the center of the cluster. In this way they destroy any subclusters that might be present, but keep the global properties (such as richness, central concentration, R_cluster) the same. They then construct the normal morphology-density relation for the scrambled clusters and compare it to the relation for the real clusters. The two diagrams are essentially identical, indicating that the morphology-density relation is controlled by global conditions rather than subclustering. Sanromà and Salvador-Solé are careful to point out that this does not imply that there are not subclusters, but only that they do not appear to play an important role in determining the morphological type of the galaxies. One useful extension of the Sanromà and Salvador-Solé study would be to repeat the test using only the clusters which show the strongest subclustering. In the regular clusters, no difference would be expected between the morphology-density relation for the randomly scrambled clusters as compared to the observed clusters. The inclusion of these regular clusters may therefore dilute any difference that may actually exist if only the clusters with strong subclustering were included.

In summary, the range in the percentages of elliptical, S0, and spiral galaxies is as great, or slightly greater when various global parameters (e.g., clustercentric position or local binding energy) are used as the independent parameter as when local galaxy density is used. It is therefore impossible to clearly determine which is the fundamental correlation, or whether some combination of global and local mechanisms are responsible for determining the morphology of galaxies in clusters.