4.3. Evidence for Tidal Stripping in Compact Groups

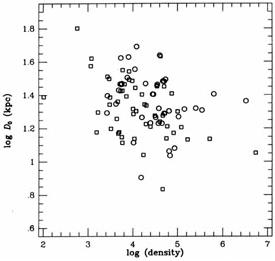
Hickson, Richstone, and Turner (1977) found a good correlation between the size of the largest galaxy and the intergroup separation for 18 compact groups, using visual estimates of the size from the Palomar Sky Survey plates. Zepf and Whitmore (1990b) have examined new CCD photometry published by Hickson, Kindl, and Auman (1989) to check this effect. Figure 4 shows a plot of the log of the diameter of the largest group member vs. the log of the density of the group. A weak trend is apparent, with a 99.9% confidence of being real, but the correlation is not nearly as obvious as the earlier results from Hickson, Richstone, and Turner. Most of the correlation is in the spirals (correlation coefficient = 0.45) rather than the elliptical and S0 galaxies (correlation coefficient = 0.24). A similar result is found when all the galaxies in the compact groups are included, rather than just the largest group members.

Figure 4. The log of the diameter of the largest compact group member vs. the log of the group density, using data from Hickson, Kindl, and Auman (1989). Squares represent spiral galaxies; circles represent elliptical and S0 galaxies. (from Zepf and Whitmore 1990b)

It would be reassuring to find evidence of a diffuse background of tidal debris in compact groups, as appears to be the case in clusters. Rose (1979) made such a search in two groups with negative results. This lead him to conclude that compact groups are only a transient unbound configuration that occasionally forms from the looser groups which surround the compact groups. However, Hickson and Rood (1988) has convincingly argued that the galaxies in compact groups are physically related based on a growing number of observational studies. In addition, Williams and van Gorkom (1988), and Williams, McMahon, and van Gorkom (1989) find that in three of the four groups they studied the HI contours clearly follow a roughly spherical contour encompassing the whole group. New CCD photometry by Rubin, Ford, and Hunter (1989) also indicates that some groups contain a common envelope.