The redshift (or blueshift) of a galaxy is the shifting of its spectral features to longer (or shorter) wavelengths primarily due to the combination of Doppler motions and the general expansion of the Universe. More properly, the term radial velocity is used primarily for the Doppler motions, which are usually the result of gravitational interactions, while redshift is reserved for the cosmological effects, although it is not generally possible to separate out cosmological expansion and Doppler velocities except for nearby galaxies and those known to be members of galaxy clusters.
Redshift, z, is defined in wavelength as
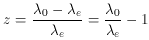
where the subscripts o and e refer to observed and emitted. In the frequency domain, redshift is defined as

The dichotomy between these formulae is due to the fact that redshift causes wavelengths to increase and frequencies to decrease.
The redshift of any given galaxy can be decomposed as

where zH is the cosmological redshift due to Hubble expansion, and zphysical is the redshift due to the physical motion of the object with respect to the observer. In an expanding universe, the cosmological redshift is always positive (objects are always redshifted). The gravitational redshift zgrav for galaxies and quasars is usually neglected since it is a very small part of the observed redshift in almost every case. The physical motions of galaxies with respect to their neighbors or the general expansion of the Universe can produce both redshifts and blueshifts, depending on whether the induced motion is away from or towards the observer, respectively.
Physical motions are most often gravitational in nature, such as the orbital motion of the Earth around the Sun. The Earth is in a nearly circular orbit around the Sun at a velocity of ~29.7 km/s. An observer at the outskirts of the Solar system and in the plane of Earth's orbit would see the velocity of the Earth relative to the Sun vary sinusoidally between +29.7 and -29.7 km/s. On cosmological scales, physical velocities are also generally caused by the orbital motions of galaxies around each other or around a common center of mass such as the deep potential well of a cluster of galaxies. The largest extragalactic physical velocities seen in the nearby universe are found for galaxies orbiting in clusters of galaxies (~1500 km/s or z = 0.005), kinematics in the central regions of quasars and active galactic nuclei (~10,000 km/s or = 0.035, and our Galaxy's motion with respect to the Cosmic Microwave Background reference frame (~630 km/s, z = 0.002)
Outside the nearby Universe, redshifts or apparent radial velocities are dominated by the cosmological expansion. This expansion is properly described as the stretching of the metric or yardstick. In the standard mathematical description of cosmology, the Friedmann-Lemaitre model, distances are defined in terms of the Robertson-Walker metric, which is the most general mathematical description for a uniform, homogeneous space that is expanding or contracting:

for spherical coordinates r, theta, phi, and time coordinate ct. R(t) is the scale factor, a function of time that is specified by the laws of gravity, and k is the curvature constant, being -1, 1, or 0 for an open, closed, or flat space geometry.
In an expanding universe, the cosmological redshift of an object is directly related to its distance. The Proper Distance to an object is the integral of the scale factor over the metric:

which reduces to the standard redshift-distance relation

where

is the Hubble Constant, named for the discoverer of the expansion of the Universe. The form of this equation is the reason that redshift is often quoted as apparent radial velocity, cz. Note that there is no special relativistic 1/(1+ v2/c2) correction applied -- apparent radial velocity is just cz.
There are also several other definitions of distance based on physical properties of objects, including luminosity distance and angular diameter distance. These are also described in any specific cosmological model in terms of the redshift and the scale factor R(t), and can be found in most textbooks on mathematical cosmology.
The first significant extragalactic redshift was that of the Andromeda galaxy (M31) measured by Vesto Slipher in 1912. Edwin Hubble discovered the empirical linear correlation between redshift and distance for nearby galaxies in the late 1920s, although we now know that Hubble's original redshift-distance relation, 600 kilometers per second per Megaparsec, was nearly a factor of ten too steep -- today's value lies near ~70 km/s/Mpc.
Redshifts are determined spectroscopically by measuring the shift of spectral features of known wavelength and frequency. This is usually done by measuring individual lines such as the 21-cm emission line of neutral hydrogen in the radio, or the strong absorption features found in the atmospheres of cool giant stars that dominate the optical spectrum of most galaxies, or by cross-correlating the galaxy spectrum with a template spectrum of a similar star or galaxy at known redshift. It is also possible to "estimate" the redshift of a galaxy from its overall spectral energy distribution if its morphological type is known. These "photometric" redshifts are substantially less accurate than spectroscopic redshifts, but may be sufficient for the scientific problem at hand.
Back to Guide to NED Redshift Search
Results.
Back to Help Page for NED's Velocity
Conversion Calculator.
Back to Frequently Asked Questions.