


2.1. The Standard Big Bang
To start with, I will introduce the basic tools and ideas of the standard ``Big Bang'' (SBB) cosmology. Students needing further background should consult a text such as Kolb and Turner [2]. An extensive discussion of inflation can be found in [3]. The SBB treats a nearly perfectly homogeneous and isotropic universe, which gives a good fit to present observations. The single dynamical parameter describing the broad features of the SBB is the ``scale factor'' a, which obeys the ``Friedmann equation''
in units where MP =
Here (in the comoving frame) the stress energy tensor of the matter is
given by
In the SBB, the Universe is first dominated by relativistic matter
(``radiation dominated'') with w = 1/3 which gives
The scale factor measures the overall expansion of the Universe
(it doubles in size as the separation between distant objects
doubles). Current data suggests an additional ``Cosmological
Constant'' term 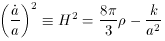
 = c = 1,
= c = 1,
 is the energy density
and k is the curvature.
The Friedmann equation can be solved for a(t) once
is the energy density
and k is the curvature.
The Friedmann equation can be solved for a(t) once
 (a) is
determined. This can be done using local energy conservation, which
for the SBB cosmology reads
(a) is
determined. This can be done using local energy conservation, which
for the SBB cosmology reads
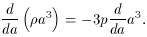
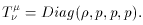

 a-4 and a
a-4 and a
 t1/2. Later the Universe is dominated by
non-relativistic matter (``matter dominated'') with w = 0 which
gives
t1/2. Later the Universe is dominated by
non-relativistic matter (``matter dominated'') with w = 0 which
gives 
 a-3 and a
a-3 and a
 t2/3.
t2/3.

 / 3 might be present on the
right hand
side of the Friedmann equation with a size similar to the other terms.
However with the
/ 3 might be present on the
right hand
side of the Friedmann equation with a size similar to the other terms.
However with the  and
k terms evolving as
negative powers of a these terms completely dominate over
and
k terms evolving as
negative powers of a these terms completely dominate over
 at the earlier epochs we are discussing here. We
set
at the earlier epochs we are discussing here. We
set  = 0 for the rest of this
article.
= 0 for the rest of this
article.