


2.2. The Flatness Feature
The ``critical density'',
 c, is defined by
c, is defined by
A universe with k = 0 has
If
The Flatness feature stems from the fact that
Figure 1. In the SBB
Despite the strong tendency for the equations to drive the Universe
away from critical density, the value of
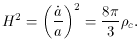
 =
=
 c and is
said to be ``flat''. It is useful to define the dimensionless density
parameter
c and is
said to be ``flat''. It is useful to define the dimensionless density
parameter
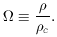
 is close to unity the
is close to unity the
 term dominates in the
Friedmann equation and the Universe is nearly flat. If
term dominates in the
Friedmann equation and the Universe is nearly flat. If
 deviates significantly from unity the k term (the ``curvature'') is
dominant.
deviates significantly from unity the k term (the ``curvature'') is
dominant.
 = 1 is an
unstable point in the evolution of the Universe. Because
= 1 is an
unstable point in the evolution of the Universe. Because

 a-3 or
a-4 throughout the history of the Universe, the
a-3 or
a-4 throughout the history of the Universe, the
 term in the
Friedmann equation falls away much more quickly than
the k / a2 term as the Universe expands, and
the k / a2 comes to dominate. This behavior is
illustrated in Fig. 1.
term in the
Friedmann equation falls away much more quickly than
the k / a2 term as the Universe expands, and
the k / a2 comes to dominate. This behavior is
illustrated in Fig. 1.
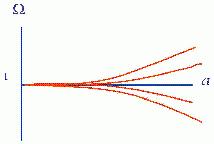
 (a) tends to
evolve away from unity as the Universe expands.
(a) tends to
evolve away from unity as the Universe expands.
 today is remarkably
close to unity even after 15 Billion years of evolution. Today the value of
today is remarkably
close to unity even after 15 Billion years of evolution. Today the value of
 is within an order of
magnitude of unity, and that means that at early times
is within an order of
magnitude of unity, and that means that at early times
 must have taken
values that were set
extremely closely to
must have taken
values that were set
extremely closely to
 c. For
example at the epoch of Grand Unified Theories (GUTs) (T
c. For
example at the epoch of Grand Unified Theories (GUTs) (T
 1016 GeV),
1016 GeV),
 has to
equal
has to
equal  c
to around 55 decimal places. This is simply an important property
c
to around 55 decimal places. This is simply an important property
 must
have for the SBB to fit the current observations, and at this point we
merely take it as a feature (the ``Flatness Feature'') of the SBB.
must
have for the SBB to fit the current observations, and at this point we
merely take it as a feature (the ``Flatness Feature'') of the SBB.