3.3. Mechanisms for producing inflation

Scalar fields play a key role in the standard mechanism of spontaneous symmetry breaking, which is widely regarded in particle physics as the fundamental origin of all particle masses. Essentially all attempts to establish a deeper picture of fundamental particles have introduced additional particles to the ones observed (typically to round out representations of larger symmetry groups used to unify the fundamental forces). Conflicts with observations are then typically avoided by giving the extra particles sufficiently large masses that they could not be produced in existing accelerators. Of course, this brings scalar fields into play.

The upshot is that additional scalar fields abound, at least in the imaginations of particle theorists, and if anything the problem for cosmologists has been that there are too many different models. It is difficult to put forward any one of them as the most compelling. This situation has caused the world of cosmology to regard the ``inflaton'' in a phenomenological way, simply investigating the behaviors of different inflaton potentials, and leaving the question of foundations to a time when the particle physics situation becomes clearer.

The challenge then is to account for at least 60 e-folding of inflation. Looking at the GUT scale (characterized by M_G M_P / 1,000) we can estimate H = sqrt[8 / 3) M_P^-2 M_G⁴], and a characteristic GUT timescale would be t_g M_G^-1. So one could estimate a ``natural'' number of e-foldings for GUT-scale inflation to be t<sub>g</sub> x H sqrt[8 / 3](M<sub>G</sub> / M<sub>P</sub>) where I have explicitly shown the Planck Mass for clarity. The upshot is that the ``natural'' number of e-foldings is a small fraction of unity, and there is the question of how to get sufficient inflation.

The ``sufficient inflation'' issue was easily addressed in the original Guth paper [1] because the end of inflation was brought on by an exponentially long tunneling process with a timescale of the form t M<sub>G</sub><sup>-1</sup> exp(B) where the dimensionless quantity B need take on only a modestly large value to provide sufficient inflation. In the Guth picture, the inflaton was trapped inside a classically stable local minimum of the inflation potential, and only quantum tunneling processes could end inflation. This type of potential is depicted in Fig. 5. The original picture proposed by Guth had serious problems however, because the tunneling operated via a process of bubble nucleation. This process was analyzed carefully by Guth and Weinberg [5] and it was show that reheating was problematic in these models: The bubbles formed with all the energy in their walls, and bubble collisions could not occur sufficiently rapidly to dissipate the energy in a more homogeneous way. The original model of inflation had a ``graceful exit'' problem that made its prediction completely incompatible with observations.

Figure 5. In the original version of inflation proposed by Guth, the potential dominated state was achieved in a local minimum of the inflaton potential. Long periods of inflation were easily produced because the timescale for inflation was set by a tunneling process. However, these models had a ``graceful exit problem'' because the tunneling process produced a very inhomogeneous energy distribution.

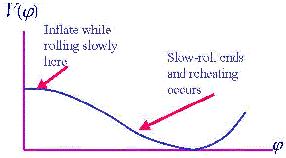
The graceful exit problem was resolved by the idea of ``slow roll'' inflation [6, 7]. In the slow roll picture inflation is classically unstable, as depicted in Fig. 6. Slow roll models are much easer to reheat and match onto the SBB. However, because the timescale of inflation is set by a classical instability, there is no exponential working to your advantage. Fine tuning of potential parameters is generally required to produce sufficient inflation in slow roll models. Essentially all current models of inflation use the slow roll mechanism. Interestingly, the constraints on the inflaton potential which are required to give the inhomogeneities a reasonable amplitude tend to exceed the constraints required to produce sufficient inflation. Thus the requirement of achieving sufficient inflation ends up in practice not providing any additional constraint on model building.

Figure 6. In ``new'' inflation a classical instability ends inflation. This allows for a graceful exit, but makes it more of a challenge to get sufficiently long inflation times.

I have outlined the tunneling and slow roll pictures. While the slow roll remains the fundamental tool in all models, there are some variations that incorporate aspects of both. In some ``open inflation'' models [8] there is inflation with a tunneling instability and a brief period of further inflation inside the bubble after tunneling. This arrangement can produce values of which are not necessarily close to unity. Also, inflation has been studied in a multi-dimensional inflaton space where there are some barriers and some slow roll directions.