3.2. A simple inflationary cosmology: Solving the problems

In the early days the inflationary cosmology was seen as a small modification of the SBB: One simply supposed that there was a period (typically around the GUT epoch) where the Universe temporarily entered a potential dominated state and ``inflated'' exponentially for a period of time. Things were arranged so that afterwards all the energy coupled out of V() and into ordinary matter (``reheating'') and the SBB continued normally.

This modification on the SBB has a profound effect on the cosmological problems. I will address each in turn:

Flatness: The flatness problem was phrased in terms of the tendency for the k term to dominate the term in the Friedmann equation (Eqn. 1). During inflation with = const. the reverse is true and the k term becomes negligible, driving the Universe toward critical density and = 1. This process is illustrated in Fig. 3.

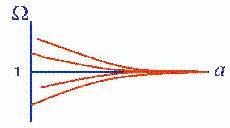
Figure 3. During inflation = 1 is an attractor.

Horizon: A period of inflation radically changes the causality structure of the Universe. During inflation, each causally connected region is expanded exponentially. A suitable amount of inflation allows the entire observed Universe to come from a region that was causally connected before inflation, as depicted in Fig. 4. Typically one needs the Universe to expand by a factor of around e⁶⁰ to solve the Horizon and Flatness problems with GUT epoch inflation.

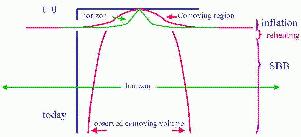
Figure 4. During inflation one horizon volume is exponentially expanded. Today, the observe region can occupy a small fraction of a causal volume.

Homogeneity: Of course ``solving'' the Horizon problem does not guarantee a successful picture. Bringing the entire observable Universe inside one causally connected domain in the distant past can give one hope that the initial conditions of the SBB can be explained by physical processes. Still, one must determine exactly what the relevant physical processes manage to accomplish. While the result of inflation is clearcut in terms of the flatness, it is much less so in terms of the homogeneity. The good news is that a given inflation model can actually make predictions for the spectrum of inhomogeneities that are present at the end of inflation. However, there is nothing intrinsic to inflation that predicts that these inhomogeneities are small. None the less, the mechanics of inflation can be further adjusted to give inhomogeneities of the right amplitude. Interestingly, inflation has a lot to say about other aspects of the early inhomogeneities, and these other aspects are testing out remarkably well in the face of new data. There will be more discussion of these matters in Sections 3.5 and 4.

Monopoles: The original Monopole problem occurs because GUTs produce magnetic monopoles at sufficiently high temperatures. In the SBB these monopoles ``freeze out'' in such high numbers as the Universe cools that they rapidly dominate over other matter (which is relativistic at that time). Inflation can get around this problem if the reheating after inflation does not reach temperatures high enough to produce the monopoles. During inflation, all the other matter (including any monopoles that may be present) is diluted to completely negligible densities and the overall density completely is dominated by V(). The ordinary matter of the SBB is created by the reheating process at the end of inflation. The key difference is that in a simple SBB the matter we see has in the past existed at all temperatures, right up to infinity at the initial singularity. With the introduction of an inflationary epoch, the matter around us has only existed up to a finite maximum temperature in the past (the reheating temperature). If this temperature is on the low side of the GUT temperature, monopoles will not be produced and the Monopole Problem is evaded.