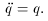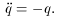4.2. A toy model
During the ``outside RJ'' regime, there is one growing and one decaying solution. The simplest system which has this qualitative behavior is the upside-down harmonic oscillator which obeys:
The phase space trajectories are show on the left panel in
Fig. 7. The system is unstable against the
runaway (or growing)
solution where |q| and |p| get arbitrarily large (and
p and q have the
same sign). This behavior ``squeezes'' any initial region in phase
space toward the diagonal line with unit slope. The squeezing effect
is illustrated by the circle which evolves, after a period of time,
into the ellipse in Fig. 7.
The simplest system showing oscillatory behavior is the normal
harmonic oscillator obeying
This phase space trajectories for this system are circles, as shown in
the right panel of Fig. 7. The angular position
around the circle corresponds to the phase of the oscillation. The effect of
having first squeezing and then oscillation is to have just about any
phase space region evolve into something like the dotted ``cigar'' in
the right panel. The cigar then undergoes rotation in phase space,
but the entire distribution has a fixed phase of oscillation (up to a
sign). The degree of phase coherence (or inverse ``cigar thickness'') is
extremely high
in the real cosmological case because the relevant modes spend a long
time in the squeezing regime.