|
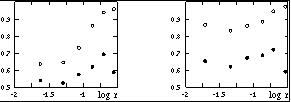
Figure 3. Ellipticity profiles for collisionless (left) and dissipative (right) versions of the same merger remnant. Open circles represent b / a, filled circles c / a. |



3.2. Dissipative Mergers
By producing inflows, dissipation can dramatically deepen galactic potential wells, and these deeper wells seem to influence the dynamics of collisionless material (eg., Katz & Gunn 1991, Udry 1993, Dubinski 1994, BH96). But these studies mostly examined effects of dissipation on dark halos; only the last one focused on disk-galaxy mergers, and that work compared but one pair of carefully-matched simulations.
The two remnants compared by BH96 were produced by mergers of equal-mass bulge/disk/halo galaxies. Both experiments started with exactly the same initial conditions, using disk inclinations of 0° and 71°; both were evolved with the same spatial resolution (a.k.a. ``force softening''). In the dissipative version, a tenth of the disk mass was treated as gas with a cooling cut-off at Tc = 104 K, while in the collisionless version everything obeyed the collisionless Boltzmann equation.

|
Figure 3. Ellipticity profiles for collisionless (left) and dissipative (right) versions of the same merger remnant. Open circles represent b / a, filled circles c / a. |
Figure 3 compares the ellipticity profiles of these two
remnants. Beyond their half-light radii (rhl  0.18
model units) both remnants are nearly oblate and rotate rapidly in
memory of the direct (i = 0°) disks used in the initial
conditions. But inside rhl the two remnants are quite
different; the collisionless version is a triaxial ellipsoid rapidly
tumbling about its minor axis, while the dissipative version is fairly
oblate and slowly rotating.
0.18
model units) both remnants are nearly oblate and rotate rapidly in
memory of the direct (i = 0°) disks used in the initial
conditions. But inside rhl the two remnants are quite
different; the collisionless version is a triaxial ellipsoid rapidly
tumbling about its minor axis, while the dissipative version is fairly
oblate and slowly rotating.
How does dissipation influence the shape of merger remnants? The dissipative remnant has a deeper potential well as a result of its central gas cloud, which contains ~ 4.5% of the luminous mass, or ~ 0.9% of the total. But the finite resolution of the force calculation spreads this central mass over a radius of ~ 0.04, rhl; thus compared to a black hole or singular logarithmic potential, this mass may be ineffective at scattering box orbits (Valluri, these proceedings). Moreover, the oblate shape of the remnant seems to be established at the moment of the merger itself instead of developing progressively from the inside out (Ryden, these proceedings).
Thinking that the shapes of these remnants might be constrained by the scarcity of box orbits, I constructed a composite mass model with the density profile of the dissipational remnant and the ellipticity profile of its collisionless counterpart, and used its potential to evaluate the phase-space volumes of the major orbit families (Barnes 1998). While this composite offered fewer boxes and more z-tubes than the collisionless remnant, bona-fide box orbits were present at all binding energies. Thus self-consistent equilibria as centrally concentrated as the dissipational remnant and as flattened as the collisionless remnant may exist. However, some finesse is probably required to realize such equilibria. Merging sows stars far and wide across phase space; not all physically consistent systems may be constructed with such a blunt instrument.
All of this work is based on only one pair of simulations, and the two remnants compared by BH96 may not be entirely typical. For example, the pre-merger disks in these experiments developed bars, and the bars in the dissipational version had significantly higher pattern speeds. Thus when the disks merged, their bars had different orientations, and this might influence remnant structure. Comparison of a larger sample of collisionless and dissipative merger remnants is clearly warranted, but sufficient computer power is hard to find. Meanwhile, collisionless mergers between models of various central concentrations may help expose the connection between density profile and remnant shape (Fulton & Barnes, in preparation).