


4. SIMULATIONS OF STARBURST GALAXIES
The crude treatment of gas thermodynamics in most work to date is
perhaps the greatest barrier to simulating star formation in
interacting galaxies. As described in
Section 2, radiative cooling is
typically cut off at 104 K, and most of the gas remains
close to this temperature. Stars, on the other hand, form at much
lower temperatures; consequently, sites of star formation can't be
directly located in the simulated gas.
Within the framework of most simulations, gas density is the only
variable with an interesting range of values, so most treatments
assume the star formation rate is a function of the gas density. This
approach has some justification; studies of star formation in systems
ranging from quiescent disk galaxies to violent starbursts find that
star formation rates roughly follow a
Schmidt (1959)
law of the form
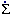 s
s 
 gn,
where
gn,
where  s and
s and  g are
the stellar and gaseous surface densities, respectively, and the index
n
g are
the stellar and gaseous surface densities, respectively, and the index
n  1.4 ± 0.15 (eg.,
Kennicutt 1998).
The usual approach is
thus to adopt a star formation law of the form
1.4 ± 0.15 (eg.,
Kennicutt 1998).
The usual approach is
thus to adopt a star formation law of the form  s
s 
 gn, where
gn, where  s and
s and  g are the stellar and gaseous
volume densities, respectively.
g are the stellar and gaseous
volume densities, respectively.
The implementation of feedback effects due to stellar evolution and
supernovae is particularly difficult. Cooling is so rapid that the
otherwise plausible strategy of dumping thermal energy into the gas
proves ineffective; the energy is radiated away before anything else
can happen
(Katz 1992,
Summers 1993).
Another trick is to impart some
outward momentum to gas particles surrounding sites of star formation
and/or supernovae; this seems more effective, but involves an
arbitrary efficiency factor
(Navarro & White 1993,
Mihos & Hernquist 1994).
It's unlikely that feedback can be properly implemented as
long as the gas is effectively treated as a single-phase medium.
A promising alternative to density-driven star formation is now available
(Gerritsen & Icke 1997).
In this approach the gas is
allowed to cool below 104 K, and sites of star formation are
defined by a Jeans criterion. The stellar radiation field, calculated
in the optically thin limit, is used to heat the gas. Star formation
is thus a self-regulating process; negative feedback maintains the
system in a quasi-stable state while slowly converting gas to stars.
Competition between radiative heating and cooling creates a two-phase
medium with temperatures of 102 K and 104 K; a
third phase at 106 K appears when the effects of supernovae
are included. As a bonus, the resulting star formation obeys a
Schmidt law with index n  1.3.
1.3.
It may turn out that many of the desirable features of this approach
are simple consequences of combining radiative cooling and negative
feedback. Some details surely require modification; the treatment of
the radiation field seems particularly suspect since galactic disks,
edge-on, are not optically thin. But the general view of star
formation as a self-regulating process and the re-introduction of gas
temperature as a physically interesting variable are surely major
improvements on previous treatments.
Does the treatment of star formation make a real difference in the
outcome of simulations? In at least one respect, it does.
Simulations using the Schmidt law predict that interacting late-type
disk galaxies consume most of their gas shortly after their first
passage; merger-induced starbursts only result if the disks are
protected from bar formation by compact central bulges
(Mihos & Hernquist 1996).
In contrast, simulations using self-regulated star
formation predict that bulgeless disk galaxies retain enough gas to
fuel ultra-luminous starbursts during their final mergers; while star
formation rates increase after the first passage, radiative heating
delays violent star formation until the merger drives most of the gas
into a compact central cloud
(Gerritsen 1997).
To date, outflows like those seen in interacting starburst galaxies
have not been reproduced with either treatment of merger-induced star
formation. This,This remains an important challenge for the future.



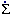 s
s 
 gn,
where
gn,
where  s and
s and  g are
the stellar and gaseous surface densities, respectively, and the index
n
g are
the stellar and gaseous surface densities, respectively, and the index
n  1.4 ± 0.15 (eg.,
Kennicutt 1998).
The usual approach is
thus to adopt a star formation law of the form
1.4 ± 0.15 (eg.,
Kennicutt 1998).
The usual approach is
thus to adopt a star formation law of the form  s
s 
 gn, where
gn, where  s and
s and  g are the stellar and gaseous
volume densities, respectively.
g are the stellar and gaseous
volume densities, respectively.


