C. A Model for the Jet Kinematics

In this section I derive various constraints on the jet kinematics, and build a possible model for the jet. Some ingredients of the model have already been discussed in Section 2.A., where morphological considerations lead to a picture where the inner jet represents a high Mach number supersonic flow (knots D, E, F, and I), the jet's Mach number is reduced (slowed) at shocks in the transition region (knots A, B, and C), and finally the outer jet (knots G, H, lobes, etc.) is a region of unstable subsonic flow.

In section 2.C. we presented evidence for apparent motions in the jet, and these can be used to constrain both the speed and direction of motion for these features. Since it is possible that the visible "patterns" in the jet and the jet "fluid" move with different speeds (e.g., Lind and Blandford 1985), we consider the pattern and fluid speeds, _pattern and _fluid, separately. The usual relationship for superluminal motion (Blandford and Königl 1979b),

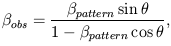
can be used to derive constraints on the pattern speed _pattern and angle between the direction of motion and the line of sight from the observed speed _obs, where all speeds are in units of the velocity of light. For example, the observed speeds of knot A, and the fastest features in knots B and D, yield lower limits on _pattern of 0.48c, 0.78c, and 0.95c, and lower limits on the Lorentz factor _pattern of 1.1, 1.6, and 3.2, respectively. The observed speeds here for knots A and B are not large enough to constrain , but the speed for the fast region of knot D requires _D < 37° ± 5°, where the uncertainty results from the formal uncertainty on the observed proper motion. Since this feature in knot D is seen to move directly away from the nucleus, it seems reasonable to assume its motion is along the jet axis, and hence the jet axis is positioned within about 37° of the line of sight (_{jet axis} ~ 37°).

An additional constraint can be garnered from the sharp feature or "edge" seen in knot A. Presumably this edge is a two-dimensional structure seen apparently edge-on. To see this sharp edge, the photons traveling toward the observer must remain within the plane of the structure as both they, and the two-dimensional structure itself, move. This constraint requires _pattern ~ cos (Biretta, Owen, and Hardee 1983; Eichler and Smith 1983); otherwise, relativistic aberration will cause the plane containing the two-dimensional structure to appear less "edge-on," or even "face-on." A more generalized geometry might allow the plane containing the edge to be at some angle 90° + to the jet axis (Reid et al. 1989; BOC89) and the resulting constraint is

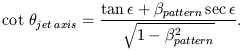
The observed angle between the edge and the jet axis measured on the plane of the sky is ~ 72°, suggesting || could be at least 18°; we will adopt || 30° as a limiting value. This constraint from the aberration of knot A is plotted in Figure 21, along with constraints from the observed proper motion of knot A's edge and the fast feature in knot D. The two constraints for knot A's edge result in 35° and _pattern ~ 0.4 for knot A. Assuming the jet axis is straight between knots D and A, and combining their constraints, we estimate that the jet axis is about 40° from the line-of-sight (_{jet axis} ~ 40°).

Figure 21. Constraints on the angle between the jet axis and line-of-sight () and pattern speed of jet features (pattern) derived from (a) observed motion of knot A edge at obs = 0.457c, (b) appearance of sharp edge in knot A together with relativistic aberration (|| < 30°), and (c) observed motion of fast feature in knot D at obs = 3.0c. The knot A constraints together require > 35°, while that from knot D requires < 54°. Taken together these yield ~ 40°.

So far we have considered only the pattern speeds of features in the jet. The more interesting parameter is the speed of the jet fluid itself. Here the arguments are unfortunately less direct. Non-relativistic numerical simulations of jets (e.g., Norman, Winkler, and Smarr 1984) have found that the fluid speed tended to be at least twice that of the visible patterns. From the derived pattern speeds _pattern 0.5 in much of the jet, this would appear to imply at least _fluid 0.5, and perhaps _fluid ~ 1 if relativistic effects can be ignored. Other indirect evidence can be taken from statistical studies of superluminal quasars, where Cohen (1990) finds similar mean values for the Lorentz factors of the fluid and pattern.

We also note that "scissor effects," which are sometimes cited as a possible cause of _pattern > _fluid (e.g., Hardee and Norman 1989; Fraix-Burnet 1990), must be relatively unimportant in the M87. A scissor effect might be created, for example, at the intersection of a pair of shock waves. While the individual waves might move slowly, their intersection point could, in principle, attain any speed. However, we note the moving features in knots D and A show motion directly down the jet. And while outward motion is seen in at least eight regions, no regions show significant inward motion. It would seem contrived if the observed motions, and especially those in knots D and A, were produced by the intersection of shock waves, rather than some mechanism closely tied to the jet flow.

A constraint on the fluid speed may also be derived from the ratio of jet to counter-jet brightness and the usual formulae for relativistic beaming (Blandford and Königl 1979b). As we have seen (Sec. 2.D.) there is considerable evidence for the presence of a counter-jet of some sort. If we assume it has an intrinsic brightness equal to that of the visible radio jet, and use the limit on the brightness ratio R > 150 derived from 15 GHz VLA observations (BOC89) we have

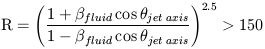
which may be solved for the limits _fluid > 0.76 (_fluid > 1.5) and _{jet axis} < 40°. We note that the stronger ratio R > 450 from optical measurements (Stiavelli, Möller, and Zeilinger 1992) produces slightly weaker limits on the derived parameters, because of the steeper optical spectral index. If a shock in knot A does reduce the fluid speed, as we have suggested, it maybe necessary to treat the "inner jet" and "transition region" separately, and this gives slightly weaker limits for each region than given above. The main uncertainty with these calculations, of course, is the assumption that the unseen counter-jet has an intrinsic brightness similar to the visible jet. It is possible they have intrinsic differences, or that there are apparent differences caused by rapid evolution and time delay between the jet and more distant counter-jet.

Finally, we have a brief look at the kinematics of knot A under the assumption that it is a strong shock. If we presume that the fluid speed of the inner jet is not too different from the derived pattern speed of the fast region in knot D, then we have _fluid 3 for the inner jet. Knot A must therefore be treated as a relativistic shock, for which material has a downstream velocity of c/3 relative to the shock (Blandford and Rees 1974). When added to the observed motion of knot A, and assuming _{jet axis} ~ 40°, we obtain an apparent speed of 0.9c for the material in the downstream region. This is at least roughly consistent with speeds in 4 out of 5 regions of knot B, which range from O.6c ± 0.2c to 1.3c ° 0.2c.

Therefore, to summarize our proposed model of the kinematics (Fig. 22): The inner jet (nucleus to knot A) is a high Mach number flow with a Lorentz factor 3 and oriented about 40° from the line-of-sight. There is a shock at knot A, about 1 kpc from the nucleus, where the flow speed is reduced to _fluid ~ 1.4 relative to the nucleus. A second shock in knot C further reduces the jet speed such that beaming becomes relatively unimportant, and at larger distances the jet is a subsonic, buoyant plume. It seems virtually certain that a counter-jet is present, though of course, details of its structure are unknown. This model is built upon, and explains, the following evidence: (1) overall jet morphology, consisting of straight inner jet (< 1.0 kpc), gradual bending in transition region, and sharp bends in outer jet (> 1.6 kpc); (2) presence of transverse features in knots A and C; (3) magnetic field normal to jet axis in knots A and C; (4) superluminal speeds up to 3c for knot D; (5) motion and appearance of sharp edge in knot A; (6) lower observed speeds in most of knot B (0.6c to 1.3c); and (7) symmetric source structure (i.e. two-sided structure) on scales 2.0 kpc. It is interesting to reflect that many elements of this model are suggested in early papers (e.g., Rees 1978).

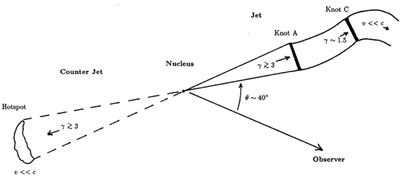
Figure 22. Suggested model for M87 jet and counter-jet. Initially the jet is relativistic with 3, but then slows in knots A and C to v << c ( ~ 1). The jet axis is oriented about 40° from the line of sight. The counter-jet is invisible over much of its length due to relativistic beaming, and perhaps intrinsic faintness as well. At the hotspot it is slowed and becomes visible.

A model of this type may have several additional benefits. As mentioned in Section 3.B., time dilation effects associated with relativistic flow along the inner jet might allow energetic electrons to travel farther from the nucleus, thereby reducing the particle lifetime problem posed by the optical emission. The knot spectra are similar until knot A, at which point they steepen systematically with increasing distance - which could be attributed to a sudden reduction in the jet velocity knot A. In terms of other FR-I radio sources, a relativistic "inner jet" might account for the one-sided jet "bases" seen in many of these sources (Bridle 1986). These one-sided bases are typically straight, well collimated, and 2 to 20 kpc in length (e.g., Bridle 1984; Eilek et al. 1984; Leahy, Jagers, and Pooley 1986; O'Dea and Owen 1986), and thus resemble the inner jet of M87. Only on larger scales does the structure become two-sided and poorly collimated, and suggests non-relativistic flow (e.g., Scheuer 1987). Furthermore, a relativistic inner jet would be consistent with 5 on the parsec scale, as required by unified models which propose that FR-I radio sources are the parent population of BL Lac objects (Urry, Padovani, Stickel 1991, and references therein). We note that _fluid 5 is not ruled out by our observations, and that such regions would appear very dim due to beaming and _{jet axis} ~ 40°.

One concern about the model proposed here is the slow velocity seen in the nucleus by VLBI techniques. Component N2 appears to move outward at only ~ 0.3c (Reid et al. 1989). This could be attributed to _pattern << _fluid, but this makes M87 rather different from quasar nuclei where _pattern ~ _fluid seems common, although cases of "slow" features are not unknown (Shaffer and Marscher 1987). Also, the large angle we propose between the jet axis and line of sight would make any features with _{pattern fluid} 5 appear very dim. Future VLBI monitoring may clarify this situation, if as components are seen in the M87 nucleus. Another concern regards the disposition of the inner jet's bulk kinetic energy after knot A. If the jet is suddenly decelerated at knot A, where is this energy going? It does not seem to go into radiation, since the luminosity of knot A is not that much greater than the other knot's; and the jet remains collimated, so it probably does not go into internal pressure. However, it is unclear how much kinetic energy is being carried by the inner jet; it is possible that the jet is very light (i.e. low mass density) and therefore carries relatively little bulk kinetic energy. A related concern is the high luminosity of the lobes, which is presumably supplied by the jet. However, this luminosity is dominated by low frequency radio emission, and these electrons have extremely long lives. It may be adequate to merely supply energetic electrons, rather than bulk kinetic energy, to the lobes. If we ignore adiabatic expansion, and assume luminous plasma flowing through knot B at ~ 0.7 merely inflates the lobes, then the lobe luminosity could be supplied in 10⁵ years (which is less than electron lifetimes at low radio frequencies).