


Although the CMBR is close to being an isotropic and thermal radiation background with simple spectral and angular distributions, it is useful to recall the formalism needed to deal with a general radiation field, since the details of the small perturbations have great physical significance. The notation used here is similar to that of Shu (1991), which may be consulted for more detailed descriptions of the quantities employed.
The state of a radiation field can be described by
distribution functions f (r,p,t), such that
the number of photons in real space volume d3r
about r and momentum space volume d3p
about p at time t with
polarization
(r,p,t), such that
the number of photons in real space volume d3r
about r and momentum space volume d3p
about p at time t with
polarization  (= 1 or 2) is
f
(= 1 or 2) is
f d3r d3p. This
distribution function is related to the photon occupation number in
polarization state
d3r d3p. This
distribution function is related to the photon occupation number in
polarization state  ,
n
,
n  (r,p,t), by
(r,p,t), by
and to the specific intensity in the radiation,
I
where k
If the occupation number is of Planck form
then the radiation field has the form of (1).
The number density of photons in the Universe is then
from which can be calculated the baryon to photon number ratio,
Similarly, the energy density of the radiation field is
It is apparent that the errors on u
It is common for the specific intensity of a radiation field to be
described by radio-astronomers in units of brightness temperature,
TRJ. This is defined as the temperature of a thermal
radiation field which in
the Rayleigh-Jeans limit of low frequency would have the same
brightness as the radiation that is being described. In the limit of
low frequency (1) reduces to
I
Thus the brightness temperature of a thermal spectrum as described by
(1) is frequency-dependent, with a peak value equal
to the radiation temperature at low frequencies, and tending to zero
in the Wien tail.
In the presence of absorption, emission and scattering processes,
and in a flat spacetime, I
where j
The specific intensity of a radiation field may be changed in several
ways. One is to make the photon distribution function anisotropic,
for example by the Doppler effect due to the peculiar motion of the
Earth relative to the sphere of last scattering, which causes the
radiation temperature becomes angle-dependent
but otherwise leaves the form of (15) unchanged.
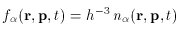
 (k,
(k, 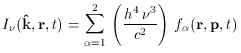
 is the photon frequency,
and h and c
are Planck's constant and the speed of light. The meaning of the
specific intensity is that the energy crossing area element dS
in time dt from within solid angle d
is the photon frequency,
and h and c
are Planck's constant and the speed of light. The meaning of the
specific intensity is that the energy crossing area element dS
in time dt from within solid angle d  about k
about k  to
to  + d
+ d is
I
is
I (k
(k  d
d dt.
dt.
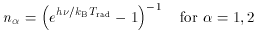

 =
nB/n
=
nB/n = 2.7 x 10-8
= 2.7 x 10-8  B
h1002. In (16)
B
h1002. In (16)  (x) is the Riemann zeta
function (
(x) is the Riemann zeta
function ( (3)
(3)  1.202)
and the value of Trad is taken
from a recent analysis of COBE data on the CMBR spectrum
(Fixsen et al.
1996).
1.202)
and the value of Trad is taken
from a recent analysis of COBE data on the CMBR spectrum
(Fixsen et al.
1996).

 and n
and n in
(16) and (17) are so small as to have no
significant astrophysical impact, and may safely be dropped.
in
(16) and (17) are so small as to have no
significant astrophysical impact, and may safely be dropped.
 = 2
KB Trad
= 2
KB Trad
 2 / c2,
so that
2 / c2,
so that
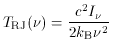
 obeys a transport equation
obeys a transport equation
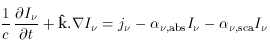
 is the
emissivity along the path (the energy emitted per
unit time per unit frequency per unit volume per unit solid angle),
is the
emissivity along the path (the energy emitted per
unit time per unit frequency per unit volume per unit solid angle),

 ,abs is the absorption coefficient (the fractional
loss of intensity of the radiation per unit length of propagation
because of absorption by material in the beam),
,abs is the absorption coefficient (the fractional
loss of intensity of the radiation per unit length of propagation
because of absorption by material in the beam), 
 ,sca
is the scattering coefficient (the fractional loss of intensity of the
radiation per unit length of propagation because of scattering by
material in the beam), and
,sca
is the scattering coefficient (the fractional loss of intensity of the
radiation per unit length of propagation because of scattering by
material in the beam), and 
 (
(
 ,abs is negative, this subtlety will not
affect the discussions in the present review. An important
property of I
,abs is negative, this subtlety will not
affect the discussions in the present review. An important
property of I that
follows from its definition (or equation 19) is that it is conserved in
flat spacetimes in the absence of radiation sources or absorbers.
that
follows from its definition (or equation 19) is that it is conserved in
flat spacetimes in the absence of radiation sources or absorbers.
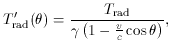
 = [1 -
(v2 / c2)]-1/2 and
= [1 -
(v2 / c2)]-1/2 and
 is the angle between the line
of sight and the observer's velocity vector
(Peebles & Wilkinson
1968).
The specific intensity may also be changed by redistributing photons
to different directions and frequencies (e.g., by scattering
processes), or by absorbing or emitting radiation (e.g., by thermal
bremsstrahlung). The choice of whether to describe these effects in
the photon distribution function, or in the specific intensity, is
made for reasons of convenience. Although the statistical
mechanics of photon scattering is often related to the
occupation numbers, n
is the angle between the line
of sight and the observer's velocity vector
(Peebles & Wilkinson
1968).
The specific intensity may also be changed by redistributing photons
to different directions and frequencies (e.g., by scattering
processes), or by absorbing or emitting radiation (e.g., by thermal
bremsstrahlung). The choice of whether to describe these effects in
the photon distribution function, or in the specific intensity, is
made for reasons of convenience. Although the statistical
mechanics of photon scattering is often related to the
occupation numbers, n , most astrophysical work is done in
the context of the specific intensity, I
, most astrophysical work is done in
the context of the specific intensity, I .
.