If the CMBR were undisturbed from the epoch of decoupling, where it picks up these ``primordial'' anisotropies from structure formation, to the present, then all perturbations in the background could be interpreted in terms of early processes in the Universe. If there are strong interactions between the epoch of decoupling and the present, then all the perturbations associated with the formation of structure might have been overwritten by later effects (e.g., from a smoothly re-ionized and dense intergalactic medium; Tegmark et al. 1994).
The true appearance of the CMBR lies between these two extremes. Even away from obvious local structures (such as stars and radio sources) there are a number of structures in the Universe that can affect the propagation of radiation. For example, gravitational lenses redistribute radiation from the epoch of recombination. Were this radiation to be isotropic, then there would be no effect from a static lens. However, a lens would affect the detailed pattern of anisotropies that are imposed on the CMBR at recombination, and detailed studies of these anisotropies should take that effect into account, especially on the smallest angular scales (e.g., Blanchard & Schneider 1987; Sasaki 1989; Watanabe & Tomita 1991). Even an isotropic radiation field may pick up anisotropies from lenses, if those lenses are not static. Examples of such effects have been discussed by Rees & Sciama (1968), Dyer (1976), Nottale (1984), Gott (1985), Gurvits & Mitrofanov (1986), and Birkinshaw (1989).
These metric (Rees-Sciama) perturbations of the isotropy of the
background radiation tend to be small, of order the gravitational
lensing angle implied by
the mass (
~ 4 G M / R c2,
where M is the object's
mass and R its size or the impact parameter) multiplied by a
dimensionless measure of the extent to which the lens is non-static.
For example, the fractional intensity change is of order
(v/c) for a lens moving across the line of sight
with velocity v. For even the largest masses (of clusters of
galaxies), for which ~ 1 arcmin),
and the largest likely velocities (~ 103 km s-1), the
fractional intensity change
I
/
I 
10-6.
It is interesting that redshift and angular effects introduced by
spatial and temporal metric variations of a perturbing mass are
closely related
(Pyne & Birkinshaw
1993),
and can be fitted into the same formalism as the Sachs-Wolfe effect
(Sachs & Wolfe 1967),
which is the dominant source of
anisotropy in the microwave background radiation on the angular scale
of the COBE experiments.
The most likely sources for metric perturbations of the CMBR are clusters of galaxies, which are the most massive well-differentiated structures in the Universe. However the structures introduced by metric effects associated with clusters of galaxies will be very difficult to see because of the presence of the Sunyaev-Zel'dovich effects, which are also introduced by clusters, but which are far more intense.
The basic physics of the Sunyaev-Zel'dovich effect is simple. Clusters
of galaxies have masses that often exceed 3 x 1014
M
,
with effective gravitational radii, Reff, of order
Mpc. Any gas in hydrostatic equilibrium within a cluster's
gravitational potential well must have electron temperature
Te given by
At this temperature, thermal emission from the gas appears in the X-ray part
of the spectrum, and is composed of thermal bremsstrahlung and line
radiation.
About a quarter of the mass of
clusters of galaxies is in the form of distributed gas (e.g.,
White & Fabian 1995;
Elbaz et al. 1995;
David et al. 1995;
Dell'Antonio et
al. 1995).
The density
of the gas is sufficiently high that clusters of galaxies are luminous
X-ray sources (e.g., Figure 2; see the reviews of
Forman & Jones 1982;
Sarazin 1988),
with the bulk
of the X-rays being produced as bremsstrahlung rather than line
radiation. Electrons in the intracluster gas are not only scattered by
ions, but can themselves scatter photons of the CMBR: for these
low-energy scatterings the cross-section is the Thomson scattering
cross-section,
The primordial and Sunyaev-Zel'dovich effects are both detectable, and
can be distinguished by their different spatial distributions.
Sunyaev-Zel'dovich effects are localized: they are seen towards
clusters of galaxies, which are large-scale structures visible to
redshifts > 0.5 in the optical and X-ray bands. Furthermore, the
amplitude of the signal should be related to other observable
properties of the clusters. Primordial structures in the CMBR are
non-localized: they are not associated with structures seen at other
wavebands, and are distributed at random over the entire sky, with
almost constant correlation amplitude in different patches of sky.
It is on the Sunyaev-Zel'dovich effects that the present review
concentrates. Although the original discussion and detection of the
effects were driven by the question of whether cluster X-ray emission
arose from the hot gas in cluster potential wells or from non-thermal
electrons interacting with magnetic fields or the cosmic background
radiation
(Sunyaev & Zel'dovich
1972),
more recently the effects have been studied for the
information that they can provide on cluster structures, on the
motions of clusters of galaxies relative to the Hubble flow, and on
the Hubble flow itself (and the cosmological constants that
characterize it). The last few years have seen many new detections of
Sunyaev-Zel'dovich effects from clusters with strong X-ray emission -
and the special peculiarity of the Sunyaev-Zel'dovich effects, that they
are redshift-independent,
and therefore almost as easy to observe at high as at low redshift,
has been illustrated by detecting clusters as distant as CL 0016+16,
at z = 0.5455, or at even higher redshift.
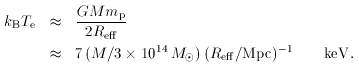
Figure 2. The central region of the ROSAT
PSPC X-ray image containing the distant cluster CL 0016+16
(z = 0.5455), showing the extended X-rays produced by the
thermal emission of gas in approximate hydrostatic equilibrium in the
cluster's potential well. The coordinates are in epoch J2000. The
data, extracted from PI bins 0.4-2.4 keV, have been background
subtracted, exposure corrected, and adaptively smoothed. The effective
spatial resolution of this image is ~ 30"
(half-power diameter). Contour levels start at a value of 1.8 x
10-4 counts s-1 arcmin-2 (75 per cent
of the average background
level) and increase by multiplicative factors of 1.94. The bright
X-ray source immediately to the north of the cluster is an AGN,
QSO 0015+162, at a redshift z = 0.554. Note
the extended source to
the southwest which is a poor cluster, RX J0018.3+1618, at a redshift
z = 0.5506
(Hughes et al. 1995).
T, so that the
scattering optical depth
e 
ne T Reff ~
10-2. In any
one scattering the frequency of the photon will be shifted slightly,
and up-scattering is more likely. On average a scattering
produces a slight mean change of photon energy
( / )
(kB Te / me
c2) ~ 10-2.
The overall change in brightness of the microwave background radiation
from inverse Compton (Thomson) scattering is therefore about 1 part
in 104, a signal which is about ten times larger than the
cosmological signal in the microwave background radiation detected by
COBE.