The distribution of photon frequency shifts caused by scattering by a
population of electrons is calculated from P (s; 
) by
averaging over the electron distribution. Thus for photons
that have been scattered once, the probability distribution of s,
P1 (s), is given by
where
The limitations of equation (33) are evident from the
assumptions made to derive equation (28). That is, the
electron distribution
pe(
If the electron velocities are assumed to follow a relativistic
Maxwellian distribution,
where
and K2(z) is a modified Bessel function of the
second kind
and second order, then the resulting distribution of photon frequency
shift factors can be calculated by a numerical integration of
equation (33).
The result of performing this calculation
for kB Te = 5.1 and 15.3 keV
is shown in Fig. 5, where it is compared with
the result given by
Sunyaev (1980).
It can be seen that
the distribution of scattered photon frequencies is significantly
asymmetric, with a stronger upscattering (s > 1) tail than a
downscattering tail. This is the origin of the mean frequency increase
caused by scatterings. As the temperature of the
electron distribution increases, this upscattering tail increases in
strength and extent.
Sunyaev's (1980)
distribution function tends to have a stronger tail at large values of
s and a larger amplitude near s = 0 than does the form
derived using (33).
It is also of interest to calculate the form of
P1 (s) for a
power-law distribution of electron energies in some range of Lorentz
factors
with normalizing constant
since such a population, which might be found in a radio galaxy lobe,
can also produce a Sunyaev-Zel'dovich effect. Synchrotron emission
from radio galaxies has a range of spectral indices, but values of
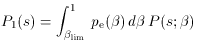
lim is the minimum value of capable of causing a
frequency shift s,
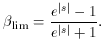
) must not extend to sufficiently large Lorentz factors,
, that the
assumptions of elastic scattering with the Thomson
scattering cross-section are violated. For photons of the microwave
background radiation these assumptions are amply satisfied provided
that 
2 x
109. In clusters of galaxies the
typical electron temperatures may be as much as 15 keV (1.8 x
108 K), but the corresponding Lorentz factors are still small, so
that we may ignore relativistic corrections to the scattering
cross-section.
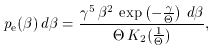
is the dimensionless
electron temperature
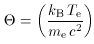
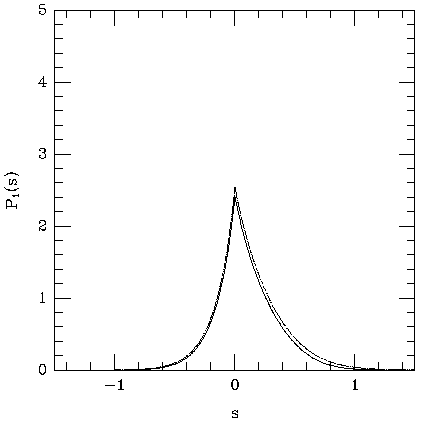
Figure 5. The scattering kernel, P1 (s), for
gases at 5.1 keV and 15.3 keV. The solid line shows the scattering
kernels calculated according to (33), as derived by
Rephaeli (1995a).
The dotted line indicates the scattering kernels as
calculated by
Sunyaev (1980),
based on the results of
Babuel-Peyrissac &
Rouvillois (1969).
1 to 2
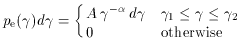
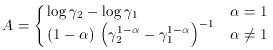
2.5 are common. Thus Fig. 6
shows the result of a calculation for an electron population with
= 2.5. As might be expected,
the upscattering
tail is much more prominent in Fig. 6 than in
Fig. 5, since there are more electrons with
>> 1 in
distribution (37) than in
distribution (35) for the values of and chosen.
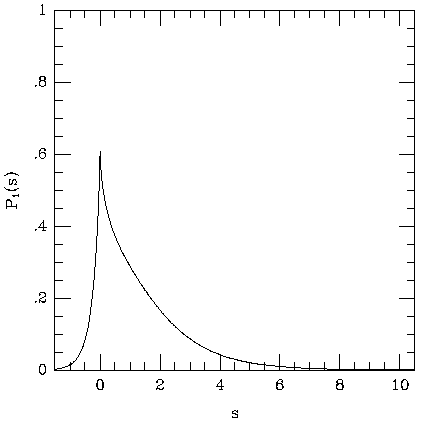
Figure 6. The scattering kernel, P1 (s), for
a power-law electron distribution with energy index = 2.5 (see
equation 37). The stronger upscattering tail here, relative to
Fig. 5, is caused by the higher proportion of
fast electrons in distribution (37) than (35).