


Finally it is necessary to use the result for the frequency shift in a single scattering to calculate the form of the scattered spectrum of the CMBR. If every photon in the incident spectrum,
is scattered once, then the resulting spectrum is given by
where P1 (
The change in the radiation spectrum at frequency
where the normalization of P1 (s) has allowed the
(trivial) integral over I0(
The integrations in (41) or (42) are
performed using the P1 (s) function appropriate
for the
spectrum of the scattering
electrons. The results are shown in Fig. 7
and 8 for two
temperatures of the electron gas and for the power-law electron
distribution. In these figures, x = h
More generally, a photon entering the electron distribution may be
scattered 0, 1, 2, or more times by encounters with the electrons. If the
optical depth to scattering through the electron cloud is
and the full frequency redistribution function from scattering is
The redistribution function Pn (s) after n
scatterings is
given by a repeated convolution
but as pointed out by
Taylor & Wright (1989),
the expression for P (s) can be written in much simpler form using
Fourier transforms, with P (s) obtained by the back transform
of
where the Fourier transform of P1 (s) is
The generalization of (41) for an arbitrary
optical depth is then
but this full formalism will rarely be of interest, since in most
situations the electron scattering medium is optically thin, with
will be sufficient (but see
Molnar & Birkinshaw
1998b).
The resulting intensity change has the form shown in
Fig. 7 or 8, but with an
amplitude
reduced by a factor
and this form of 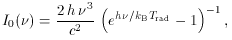
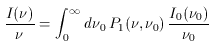
 ,
, 0) is the probability that a
scattering occurs from
frequency
0) is the probability that a
scattering occurs from
frequency  0 to
0 to  , and I(
, and I( ) / h
) / h is the spectrum
in photon
number terms. Since P1(
is the spectrum
in photon
number terms. Since P1( ,
, 0) =
P1 (s) /
0) =
P1 (s) /  , where
P1 (s) is
the frequency shift function in (33), this can be
rewritten as a convolution in s = ln (
, where
P1 (s) is
the frequency shift function in (33), this can be
rewritten as a convolution in s = ln ( /
/  0),
0),
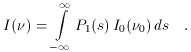
 is then
is then
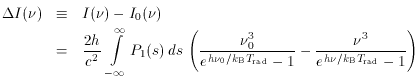
 ) to be included in (42)
to give a form that is convenient for numerical calculation.
) to be included in (42)
to give a form that is convenient for numerical calculation.
 / kBTrad is a
dimensionless frequency.
The functions
/ kBTrad is a
dimensionless frequency.
The functions  I (x)
show broadly similar features for thermal
or non-thermal electron distributions: a decrease in
intensity at low frequency (where the mean upward shift of the photon
frequencies caused by scattering causes the Rayleigh-Jeans part of the
spectrum to shift to higher frequency, and hence to show an intensity
decrease: see Fig. 1)
and an increase in intensity in the Wien part
of the spectrum. The detailed shapes of the spectra differ
because of the different shapes of the scattering functions
P1 (s)
(Figs. 5 and
6).
I (x)
show broadly similar features for thermal
or non-thermal electron distributions: a decrease in
intensity at low frequency (where the mean upward shift of the photon
frequencies caused by scattering causes the Rayleigh-Jeans part of the
spectrum to shift to higher frequency, and hence to show an intensity
decrease: see Fig. 1)
and an increase in intensity in the Wien part
of the spectrum. The detailed shapes of the spectra differ
because of the different shapes of the scattering functions
P1 (s)
(Figs. 5 and
6).
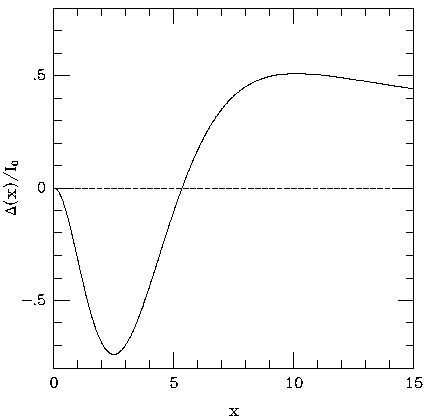
Figure 8. The fractional spectral deformation
caused by inverse-Compton scattering of an incident Planck spectrum by
a single scattering from a power-law population of electrons
with  = 2.5 (equation 37). The
spectral deformation has a similar shape to that seen in
Fig. 7, but with a deeper
minimum and more extended tail. This arises from the larger frequency
shifts caused by the higher Lorentz factors of the electrons (see
Fig. 6).
= 2.5 (equation 37). The
spectral deformation has a similar shape to that seen in
Fig. 7, but with a deeper
minimum and more extended tail. This arises from the larger frequency
shifts caused by the higher Lorentz factors of the electrons (see
Fig. 6).
 e, then the probability
that a photon penetrates the cloud
unscattered is e-
e, then the probability
that a photon penetrates the cloud
unscattered is e- e, the probability that it is once
scattered is
e, the probability that it is once
scattered is  e
e-
e
e- e,
and in general the probability of N scatterings is
e,
and in general the probability of N scatterings is
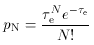
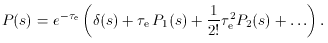
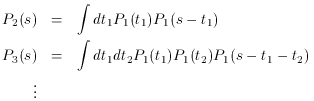
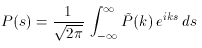
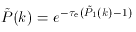
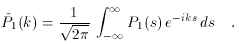
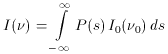
 e << 1, so that the
approximation
e << 1, so that the
approximation
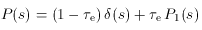
 e. This is given explicitly as
e. This is given explicitly as
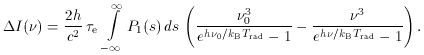
 I(
I( )
will be used extensively later. One
important result is already clear from (51): the
intensity change caused by the Sunyaev-Zel'dovich effect is
redshift-independent,
depending only on intrinsic properties of the scattering medium
(through the
)
will be used extensively later. One
important result is already clear from (51): the
intensity change caused by the Sunyaev-Zel'dovich effect is
redshift-independent,
depending only on intrinsic properties of the scattering medium
(through the  e factor
and P1 (s), and the
Sunyaev-Zel'dovich effect
is therefore a remarkably robust indicator of gas properties at a
wide range of redshifts.
e factor
and P1 (s), and the
Sunyaev-Zel'dovich effect
is therefore a remarkably robust indicator of gas properties at a
wide range of redshifts.