5. SYSTEMATIC ERRORS

There are a variety of possible systematic errors which afflict gravitational lens determinations of the Hubble constant. The first of these, which we have already mentioned, is the degeneracy between H₀ and a uniform density sheet in the lens plane. For example, suppose that there is a uniform density circular disk of matter covering all the images. This will act like a simple (Gaussian) converging lens and bring the same rays that would have met at the observer to a common focus closer to the lens. In other words, the potential variation is quadratic and so the contribution to the gravitational delay is also quadratic, just like the geometrical delay, from which it is therefore indistinguishable. It has been argued that, as any sheet must have positive mass density, we can only set an upper bound on the Hubble constant (Falco et al. 1985).

A second uncertainty is associated with the choice of cosmographic world model. Let us suppose that the universe is of homogeneous Friedmann-Robertson-Walker (FRW) type so that it is parameterized by the current density parameter ₀. The angular diameter distances to high redshift sources and lenses depend quite sensitively upon ₀. However, the combination D_dD_s / D_ds, relevant for the inferred Hubble constant, is relatively insensitive. For example, in the 0957+561 system, K = 39.9h^-1 days arcsec^-2 for an Einstein-de Sitter universe with ₀ = 1, and K = 42.9h^-1 days arcsec^-2 for an open universe with ₀ = 0.1. If we take an additional step and introduce a cosmological constant while keeping the universe flat, the change in K is even smaller. For 0 < < 1, K attains a maximum of 41.7h^-1 days arcsec^-2 in the ₀ = 0.25, = 0.75 model. In a lens system with higher redshifts, however, the choice of cosmological model is more important. We can thus use high-redshift lenses to constrain the density parameter ₀ once H₀ has been measured. For example, in the z_s = 3.62 lensed BAL quasar B1422+231, the difference in K between ₀ = 1 and ₀ = 0.1 models amounts to 24% (assuming the lens redshift of z_d = 0.65, as reported by Hammer et al. 1995).

Now let us turn to inhomogeneous cosmological models. If the universe has an overall mean density sufficient to allow it to follow FRW dynamics on the average but with this mass confined to small concentrated lumps, none of which intersect the line of sight, then individual ray congruences will be subject to zero convergence as they cannot pass through any matter. In this case, the angular diameter distance must be changed to the affine parameter (Press & Gunn 1973). If, for example, the mass in an Einstein-De Sitter universe were concentrated in large, distant lumps, then K would change by over 10% for B1422+231. However, this assumption is quite unrealistic, because the combined tidal influence of these lumps must, on the average, reproduce the cosmography of a homogeneous universe, and, in fact, it does. In what follows we assume that our line of sight is not special in this sense and that individual dark masses are small enough that we can treat them as smoothly distributed.

The next type of systematic error is starting to be taken more seriously and has broader implications. This is the error introduced in the measurement of H₀ due to large-scale structure distributed along the line of sight from the source to the observer. A simple and standard description of large-scale structure in the universe is to form the power spectrum of relative density fluctuations, P(k), that have supposedly grown from perturbations similar to those that we observe in the microwave background fluctuations. The short wavelength perturbations [k > k_m ~ (10 Mpc)^-1] have grown to non-linear strength; the long wavelength perturbations should still be in the linear regime with P(k) k. In the linear regime the potential fluctuations therefore satisfy k^-2 k^-2[k³ P(k)]^1/2 ~ constant. In fact, the potential fluctuation is not just constant with linear scale but also with time and has a value ~ 3 x 10^-5 c² as normalized to the fluctuations measured by COBE.

The perturbations that are most important for perturbing gravitational lens images are those for which k² P(k) is maximized, i.e. with k ~ k_m ~ (10 Mpc)^-1. As typical angular diameter distances are D ~ 1 Gpc, these subtend angles ~ 30', much larger than the strong lensing regions, and we expect to see N ~ k_m D ~ 100 perturbations, of both signs, along the line of sight. If we consider a single ray passing through a roughly spherical perturbation, it will be deflected through an angle ~ / c² and as there are N such deflections adding stochastically, the total deflection will ~ N^1/2 ~ 1'. (It is amusing that although that there has been so much trouble taken to point HST to a small fraction of a pixel, the universe has a pointing error of about the width of WFPC chip!) In addition, each fluctuation will introduce a propagation time fluctuation / k_m c³ ~ ( / c²)(D / Nc). These fluctuations add stochastically giving a total time difference relative to a homogeneous universe of t ~ ( / c²)(D / N^1/2c) ~ 10⁴ yr. However, none of this matters because there is no way to detect the deflection or time delay of a single ray.

The situation changes when we consider two rays separated by a small angle (Blandford & Jaroszynski 1981). On passing though a single perturbation, the angular separation will change by an angle ~ k_m (D) ( / c²). Again, summing the effects of N such fluctuations stochastically gives an estimate of the total fractional change in , a measure of the strength of both the magnification and the shear fluctuations. We obtain

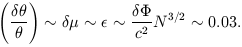
(5.31)

These fluctuations should be coherent over angles ~ (1/k_m D) ~ 30' on the sky. There have been attempts to measure this signal using the images of faintgalaxies (e.g. Mould et al. 1994).

There is a subtlety when we consider the observable time fluctuations. If the separation of a pair of rays is much less than the angular scale of the fluctuation, we can Taylor expand the potential. We have already dismissed the constant term and might expect the linear term to be observable. However, this is not the case as can be seen by noting that its effect simply deflects both rays through the same angle, just like a prism, and does not increase the optical path at all. We have to expand to quadratic order across the rays to obtain a total time difference due to the fluctuations of t ~ ( / c²) (D / N^1/2 c) (k_m D)² ~ ( / c²) N^3/2 (D² / c). Now suppose that these two rays are associated with a common source and observer in a gravitational lens. The time delay in an otherwise homogeneous universe would be t ~ D² / c and so the relative change in the arrival time will satisfy

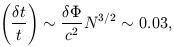
(5.32)

as above. Therefore to order of magnitude, we find that a few percent error in the derived value of the Hubble constant will be introduced by the effects of large-scale structure and the effect deserves computing seriously.

This problem has been addressed by Seljak (1994) and Bar-Kana (1996), following earlier papers by Kovner (1987) and Narayan (1991). They find three distinct effects:

(a) The images of the source, their positions and their shapes, are subject to a global shear transformation. This effect will generally be absorbed in the quadratic contribution to shear from the large-scale distribution of mass in the deflector plane.

(b) The images of the deflecting galaxies, their positions relative to the images of the source and their shapes will be subject to an additional shear. Naturally this shear is only caused by fluctuations between us and the deflector. This effect means that there is a cosmic uncertainty in the image positions which must be taken into account when we make the models.

(c) There will be quadratic potential fluctuations acting on the unperturbed rays that cause stochastic gravitational delays that create additional direct changes in the measured lags. These will translate directly into errors in H₀. There is an interesting observational possibility here. We can contemplate performing deep redshift surveys in the vicinity of the most promising lenses and rather than treat these effects as random errors, try to remove them directly.