


Any estimate of H0 derived from gravitational lensing will be no better than the lens model that is deduced from observations of the positions and fluxes of the individual images. Lens modeling is, necessarily, a rather subjective business. The procedure that has to be followed depends upon whether or not the images are resolved. In most cases, there are N unresolved point images giving 2(N - 1) relative coordinates. There are also (N - 1) relative fluxes which can be fit to the magnification ratios. Since sources are variable, fluxes must be compared at the same emission time. (A complication that can arise at optical wavelengths is that individual stars in the lensing galaxy can cause additional, variable magnification, called microlensing, if the source is sufficiently compact. However, this is unlikely to be a problem at infrared or radio wavelengths.) So, with N point images, there are usually 3(N - 1) observables which can be used in model fitting. Once the relative time delays in the system are measured, they provide (N - 2) additional constraints.
Resolved images contain more information. Firstly, when compact radio sources are resolved using VLBI, the individual images ought to be related by a simple, four parameter, linear transformation (Eq. 2.16). This can be measured and is more useful than the flux ratio alone in constraining the model, and would give an additional 3(N - 1) observables. Secondly, if the radio structure is large enough, it is possible to expand to one higher order and measure the gradient of µij. Thirdly, some sources are so extended that they form ring-like images. This can happen at either radio or optical wavelengths. In this case we have a large number, perhaps thousands of independent pixels to match up. In principle, this can lead to a highly constrained lens (and source) model. The best techniques for tackling this problem at radio wavelengths (Wallington, Kochanek & Narayan 1996) incorporate the model fitting as a stage in the map making procedure and, in some cases this can lead to impressively good models.
In order to model a simple gravitational lens, the scaled potential
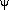 of the lensing
galaxy, (plus any additional galaxies close enough to contribute to the
deflection) is
modeled using a simple function that contains adjustable parameters that
measure the
depth of the potential, its core radius, its ellipticity and its radial
variation. A convenient
functional form is the elliptical potential
of the lensing
galaxy, (plus any additional galaxies close enough to contribute to the
deflection) is
modeled using a simple function that contains adjustable parameters that
measure the
depth of the potential, its core radius, its ellipticity and its radial
variation. A convenient
functional form is the elliptical potential
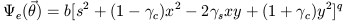
| (4.19) |
where 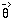 = (x, y)
measures distance from the center of the potential which is located at
(x0, y0). The two parameters
= (x, y)
measures distance from the center of the potential which is located at
(x0, y0). The two parameters
 c,
c,
 s combine to
describe the ellipticity and the position
angle of the major axis. The exponent q measures the radial
variation of the density at
large radius. A value q = 0.5 corresponds to an isothermal sphere
and a value q = 1
has asymptotically
s combine to
describe the ellipticity and the position
angle of the major axis. The exponent q measures the radial
variation of the density at
large radius. A value q = 0.5 corresponds to an isothermal sphere
and a value q = 1
has asymptotically 
 r-2 as
might be appropriate if, for example, mass traces light
as in a Hubble profile. The elliptical potential has the advantage that
it is quick to
compute and good for searches in multi-dimensional parameter space. Its
drawback is
that the corresponding surface density is peanut-shaped at large
ellipticity. Either two
potentials must be superposed to generate realistic surface density
distributions or a
choice made from a smorgasbord of more complicated potentials (e.g.
Schneider et al. 1992).
In some cases, these potentials can be located and oriented using the observed
galaxy image. However, we know that the mass in galaxies does not
completely trace the
light; in particular it diminishes more slowly with increasing
radius. Therefore, we still
have some freedom in modeling the mass distribution of lensing galaxies,
even if their
light profiles are well known. An example of the elliptical potential
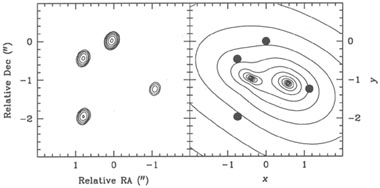
model is shown in
Fig. 2. Motivated by the optical HST images of
1608+656, two elliptical potentials are
superimposed to produce the observed quad configuration.
r-2 as
might be appropriate if, for example, mass traces light
as in a Hubble profile. The elliptical potential has the advantage that
it is quick to
compute and good for searches in multi-dimensional parameter space. Its
drawback is
that the corresponding surface density is peanut-shaped at large
ellipticity. Either two
potentials must be superposed to generate realistic surface density
distributions or a
choice made from a smorgasbord of more complicated potentials (e.g.
Schneider et al. 1992).
In some cases, these potentials can be located and oriented using the observed
galaxy image. However, we know that the mass in galaxies does not
completely trace the
light; in particular it diminishes more slowly with increasing
radius. Therefore, we still
have some freedom in modeling the mass distribution of lensing galaxies,
even if their
light profiles are well known. An example of the elliptical potential
model is shown in
Fig. 2. Motivated by the optical HST images of
1608+656, two elliptical potentials are
superimposed to produce the observed quad configuration.
|
Figure 2. Radio map of the gravitational lens system 1608+656. The system was observed on 1996 October 10 with the VLA at 8.4 GHz. The map shows four unresolved images of the background source (at zs = 1.39). The brightest image (A) is located at the origin. (Courtesy of Chris Fassnacht.) Right: A simple model for 1608+656, consisting of two elliptical potentials. Solid lines represent logarithmically spaced density contours of the lensing mass distribution. The observed image positions (marked with dots) and their relative fluxes are accurately reproduced by this model. |
It is also conventional to augment the lensing galaxy potential with a simple quadratic form,
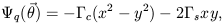
| (4.20) |
which is trace-free and corresponds to a pure shear of the images. The external shear has two origins: dark matter lying in the lens plane associated with galaxies outside the strong lensing region and large-scale structure along the line of sight, as we discuss in more detail below.
A common procedure for modeling well observed gravitational lenses is to
decide upon
a list of independent observables and a smaller number of lens model
parameters. These
parameters are then varied so as to minimize some measure of the
goodness of fit,
typically a  2 associated
with the differences in the observables as predicted by the model
from those actually measured. This approach has the merit of rewarding
simplicity.
However, the fit is usually somewhat imperfect and it is difficult to
assign a formal error. A
somewhat better approach, that is much harder to implement in practice,
is to construct
families of more elaborate models that may contain more parameters than
observables
and which are consequently underdetermined. Using this approach, it
ought to be possible
to derive many models that exactly recover the observables. We can then
assign two
types of error to the model time delay. One is associated with the
measurement errors
in the observables, the other depends upon the freedom in the models and
it is here that
the outcome depends most subjectively upon what we are prepared to countenance.
2 associated
with the differences in the observables as predicted by the model
from those actually measured. This approach has the merit of rewarding
simplicity.
However, the fit is usually somewhat imperfect and it is difficult to
assign a formal error. A
somewhat better approach, that is much harder to implement in practice,
is to construct
families of more elaborate models that may contain more parameters than
observables
and which are consequently underdetermined. Using this approach, it
ought to be possible
to derive many models that exactly recover the observables. We can then
assign two
types of error to the model time delay. One is associated with the
measurement errors
in the observables, the other depends upon the freedom in the models and
it is here that
the outcome depends most subjectively upon what we are prepared to countenance.
Let us describe some of the dangers and possibilities involved in model fitting by considering image formation in a simple case, the so-called "quad" sources. These are quadruply imaged point sources formed by a galaxy for which the circular symmetry is broken by an elliptical perturbation. (Depending upon the nature of the potential in the galaxy nucleus, there may also be a fifth, faint, central image which we shall ignore.) For illustration, we use the simplest possible model of a singular isothermal sphere potential perturbed by a quadratic shear, and work to first order in the ellipticity (cf Blandford & Kovner 1988).
We write the potential in the form
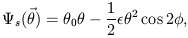
| (4.21) |
where polar coordinates
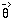 =
(
=
( ,
,
 ) refer to the center of the
potential located at the
center of the observed lensing galaxy (Fig. 3).
The first term
) refer to the center of the
potential located at the
center of the observed lensing galaxy (Fig. 3).
The first term 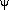 0s =
0s =
 0
0
 describes an
isothermal sphere (
describes an
isothermal sphere (

 -1), and is
circularly symmetric. The second term is the
non-circular perturbation. We assume that we know its orientation from
the shape of the
galaxy but treat the ellipticity as unknown. If we set
-1), and is
circularly symmetric. The second term is the
non-circular perturbation. We assume that we know its orientation from
the shape of the
galaxy but treat the ellipticity as unknown. If we set
 = 0 and place a source on the
axis, then the image will be a circular ring of radius
= 0 and place a source on the
axis, then the image will be a circular ring of radius
 0 known as the
Einstein ring. We now switch on the perturbation and solve for
the source position to linear order assuming
that
0 known as the
Einstein ring. We now switch on the perturbation and solve for
the source position to linear order assuming
that  << 1. We find that
the source position is
<< 1. We find that
the source position is
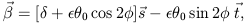
| (4.22) |
where  =
=
 -
-
 0, and
0, and
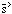 ,
,
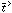 are unit vectors in the
radial and tangential directions
respectively. We can now evaluate the Hessian and find that its eigenvalues are
are unit vectors in the
radial and tangential directions
respectively. We can now evaluate the Hessian and find that its eigenvalues are
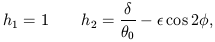
| (4.23) |
and the principal axes are rotated with respect to
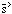 ,
,
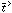 by an angle
by an angle
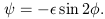
| (4.24) |
These eigenvalues are the reciprocals of the quasi-radial and
quasi-tangential magnifications,
so that the total magnification is µ =
(h1 h2)-1 =
( /
/
 0 -
0 -
 cos
2
cos
2 )-1. The locus
of the infinite magnification on the sky, the "critical curve" is then
given by h2 = 0 or
)-1. The locus
of the infinite magnification on the sky, the "critical curve" is then
given by h2 = 0 or
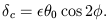
| (4.25) |
The critical curve is the image of the "caustic", the locus in the source plane of points that are infinitely magnified. Its equation is
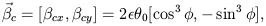
| (4.26) |
which is the parametric equation of an astroid. If we know the source
position, 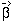 ,
and it is located within the astroid then there will be four images located
close to the critical
curve (Fig. 3). If the source lies outside the
astroid, there will be two images.
,
and it is located within the astroid then there will be four images located
close to the critical
curve (Fig. 3). If the source lies outside the
astroid, there will be two images.
This model has two free parameters,
 and
and
 0, and as we may
have eleven observables
in a four-image lens (three pairs of relative positions + three flux
ratios + two time delay
ratios), there are many internal consistency checks. For example, the
angles of the four images must satisfy
0, and as we may
have eleven observables
in a four-image lens (three pairs of relative positions + three flux
ratios + two time delay
ratios), there are many internal consistency checks. For example, the
angles of the four images must satisfy
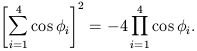
| (4.27) |
Now, in order to trust the model, we contend that it is necessary that every observable be fit within its measurement error, or there should be a good reason why it can be excused. For example, we might have a spectroscopic indication that microlensing is at work in one of the images and then we would discount the measurement of its flux.
Now, it is extremely unlikely that any lens will ever be found that is
this simple. So,
after we are sure that there is inconsistency, we must introduce
additional parameters
or change the model. Following the above approach of expanding about the
Einstein
ring, we can (or may have to) allow the center of the potential to vary,
adjust the
orientation of the perturbations, allow the ellipticity
 to vary with radius
to vary with radius
 , introduce
higher harmonics (e.g.
, introduce
higher harmonics (e.g.  cos
4
cos
4 for box-like equipotentials) and
so on. Alternatively,
we can turn to a density-based model. The nature and quality of the
observations will usually dictate this choice.
for box-like equipotentials) and
so on. Alternatively,
we can turn to a density-based model. The nature and quality of the
observations will usually dictate this choice.
What we discover when we carry out this procedure is that the allowed range of
observables is quite sensitive not just to the parameters, but to the
functional form of
the model. For example, constraint 4.27 is quite general but can be
violated if (not unreasonably) we were to add a cos
4 term. In addition, the shape of
the unperturbed,
circular potential controls the quasi-radial magnification and changing
it changes h1
to 1 - d2
term. In addition, the shape of
the unperturbed,
circular potential controls the quasi-radial magnification and changing
it changes h1
to 1 - d2 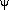 0s /
d
0s /
d 2. The
ratios of time lags are fairly well fixed by the observed image
magnifications and location; however, the absolute values (in which we
are primarily
interested) are extremely sensitive to radial variation of the
ellipticity and this can be
measured if we have very accurate image positions or an extended
source. Finally, we
should probably always include the quadratic form Eq. 4.20 to take
account of distant mass.
2. The
ratios of time lags are fairly well fixed by the observed image
magnifications and location; however, the absolute values (in which we
are primarily
interested) are extremely sensitive to radial variation of the
ellipticity and this can be
measured if we have very accurate image positions or an extended
source. Finally, we
should probably always include the quadratic form Eq. 4.20 to take
account of distant mass.
There are further possible consistency checks. For example, if we can make VLBI
observations of the individual image components, as should be possible
for 1608+656
(Myers et al. 1995,
Fassnacht et al. 1996;
Fig. 2),
and resolve structure in the radial
direction, we can also check both the radial eigenvalue
h1, and the orientation angle
 for each of the images. Even better, if we have more than one source, as
appears to be
the case in 1933+503
(Sykes et al. 1996),
than we have two independent opportunities
to test the model and derive the parameters. (This approach may also be
of interest for cluster arcs.)
for each of the images. Even better, if we have more than one source, as
appears to be
the case in 1933+503
(Sykes et al. 1996),
than we have two independent opportunities
to test the model and derive the parameters. (This approach may also be
of interest for cluster arcs.)
Let us use the quad H1413+117 for illustration and try to model it using
a simple
potential (Eq. 4.21). We can guess the lens center pretty accurately,
but not the position
angle of the major axis of the elliptical perturbation,
 0. Using Eq. 4.27, we find four
choices for
0. Using Eq. 4.27, we find four
choices for  0 and we
examine each of these in turn to try to find a consistent solution
for the source position
0 and we
examine each of these in turn to try to find a consistent solution
for the source position
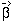 by varying
by varying
 ,
,
 0, and the lens
center. We find that none
of our choices of
0, and the lens
center. We find that none
of our choices of  0 can
accomplish this, although one comes close. However, if we
now compute the magnification ratios, we find that they are quite
inconsistent with
the observations. Therefore we can assuredly reject our lens model. It
turns out that
it is possible to reproduce the positions and fluxes using an elliptical
potential with
parameters {b, s, q,
0 can
accomplish this, although one comes close. However, if we
now compute the magnification ratios, we find that they are quite
inconsistent with
the observations. Therefore we can assuredly reject our lens model. It
turns out that
it is possible to reproduce the positions and fluxes using an elliptical
potential with
parameters {b, s, q,
 c,
c,
 s,
xc, yc} offset by an external shear
with parameters
s,
xc, yc} offset by an external shear
with parameters  c,
c,
 s.
Although this seems the most plausible model, it is not unique
(Yun et al. 1996,
preprint) and this would be a concern were this a good choice for
monitoring. Unfortunately, it is
not as the predicted time delays are almost certainly too small.
s.
Although this seems the most plausible model, it is not unique
(Yun et al. 1996,
preprint) and this would be a concern were this a good choice for
monitoring. Unfortunately, it is
not as the predicted time delays are almost certainly too small.
4.3. Uncertainties in the models
An important question that we must now address is "How do we assign a
formal error
to the predicted model on the basis of a deflector model?" One procedure
is to define a
 2 using careful values
for the measurement errors and then choose parameters
pi that
minimize this statistic. We then compute a covariance matrix
2 using careful values
for the measurement errors and then choose parameters
pi that
minimize this statistic. We then compute a covariance matrix
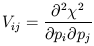
| (4.28) |
and invert and diagonalize this quantity so as to form the error
ellipsoid. We next
compute the maximum fractional change in the time delay within this
error ellipsoid and
quote this as the fractional error in the derived Hubble constant
varying the parameters
independently until  2 /
2 /
 increases by unity. The maximum
change in the derived value
of the delay as we go through this procedure is the required error in
the delay.
increases by unity. The maximum
change in the derived value
of the delay as we go through this procedure is the required error in
the delay.
However, this is still not enough because existence does not imply
uniqueness. Suppose
that we have a model that truly reproduces all the observables giving an
acceptable value
for  2 and for which the
underlying mass distribution is dynamically possible. We should
still aggressively explore all other classes of models that can also fit
the observations but
yet which produce disjoint estimates for the time delay. The true
uncertainty in the
Hubble constant is given by the union of all of these models. This is a
large task.
Clearly, we may have to introduce some practical limitations. It is
probably quite safe to
reject dynamically unreasonable mass distributions, for example positive
radial gradients
in surface density, but are we allowed to posit isolated concentrations
of unseen mass?
Of course, only time will tell whether there are genuinely dark
galaxies, but until we can
demonstrate that all significant perturbers are luminous we must allow
for this possibility.
There is already an indication that there may be more unseen mass than we have
already included in the discovery that the incidence of quad sources
relative to doubles
is much greater than one might have expected if the lenses are about as
elliptical as normal galaxies
(King & Browne 1996).
Three explanations have been advanced for this
discrepancy. Firstly, the total mass associated with the observed
lensing galaxies may be
highly elliptical, or, indeed, quite irregular. (It appears that
observed faint galaxies have
a median ellipticity of ~ 0.4 as opposed to ~ 0.15 for local galaxies.)
Secondly, many
of the lenses may actually have unseen companions so that the combined
potential will
generally be quite elliptical. Thirdly, as we discuss below, propagation
effects associated
dark matter long the line of sight may actually promote the formation of quads.
2 and for which the
underlying mass distribution is dynamically possible. We should
still aggressively explore all other classes of models that can also fit
the observations but
yet which produce disjoint estimates for the time delay. The true
uncertainty in the
Hubble constant is given by the union of all of these models. This is a
large task.
Clearly, we may have to introduce some practical limitations. It is
probably quite safe to
reject dynamically unreasonable mass distributions, for example positive
radial gradients
in surface density, but are we allowed to posit isolated concentrations
of unseen mass?
Of course, only time will tell whether there are genuinely dark
galaxies, but until we can
demonstrate that all significant perturbers are luminous we must allow
for this possibility.
There is already an indication that there may be more unseen mass than we have
already included in the discovery that the incidence of quad sources
relative to doubles
is much greater than one might have expected if the lenses are about as
elliptical as normal galaxies
(King & Browne 1996).
Three explanations have been advanced for this
discrepancy. Firstly, the total mass associated with the observed
lensing galaxies may be
highly elliptical, or, indeed, quite irregular. (It appears that
observed faint galaxies have
a median ellipticity of ~ 0.4 as opposed to ~ 0.15 for local galaxies.)
Secondly, many
of the lenses may actually have unseen companions so that the combined
potential will
generally be quite elliptical. Thirdly, as we discuss below, propagation
effects associated
dark matter long the line of sight may actually promote the formation of quads.
4.4. The double quasar 0957+561
We now briefly turn from quads to the important case of 0957+561, the only gravitational lens where the time delay has been measured with high accuracy (Kundic et al. 1997). Traditionally, 0957+561 was thought to be a difficult system to model because of the small number of constraints in its two-image configuration and because of the complexity of the lensing potential - the primary lensing galaxy G1 is surrounded by a cluster. To a large extent, these problems have been resolved in the extensive theoretical study of Grogin & Narayan (1996). The crucial set of constraints in the GN model was provided by high spatial resolution VLBI mapping of Garrett et al. (1994), which resolved inner jets in both images of the source into five centers of emission. Mapping of one jet into the other fixed the relative magnification tensor of images A and B (Eq. 2.16), as well as its gradients along and perpendicular to the jet. This, in turn, provided a tight constraint on the radial mass profile (dM / dr) at the image locations, which, together with the total enclosed mass M(< r), controls the conversion factor between the time delay and the physical distance to the lens. The importance of the dM / dr term was nicely illustrated by Wambsganss & Paczynski (1994).
The remaining model degeneracy in the 0957+561 system between the lensing galaxy G1 and its host cluster cannot be removed by using relative image positions and magnifications (Falco, Gorenstein & Shapiro 1985). It has to be broken by either directly measuring the mass of G1 via its velocity dispersion, or by measuring the surface density in the cluster from its weak shearing effect on the images of background galaxies (e.g. Tyson, Valdes & Wenk 1990, Kaiser & Squires 1993). If both of these parameters are independently determined, they provide an important consistency check on the model.
Falco et al. (1996, private communication) recently observed G1 with the LRIS
spectrograph at the Keck. Their high signal-to-noise spectrum yields a
line-of-sight velocity
dispersion roughly in the range
 obs = 275 ± 30
km/s (2
obs = 275 ± 30
km/s (2 ), consistent with the only
published measurement by
Rhee (1991),
), consistent with the only
published measurement by
Rhee (1991),
 obs = 303 ± 50
km/s. Using a deep CFHT image of the field,
Fischer et al. (1997)
mapped the cluster mass distribution from the
distortion of faint background galaxies. Adopting their estimate of the mean
background galaxy redshift (zb = 1.2) gives the
dimensionless cluster surface mass density
obs = 303 ± 50
km/s. Using a deep CFHT image of the field,
Fischer et al. (1997)
mapped the cluster mass distribution from the
distortion of faint background galaxies. Adopting their estimate of the mean
background galaxy redshift (zb = 1.2) gives the
dimensionless cluster surface mass density
 =
=
 /
/
 c = 0.18±0.11
(2
c = 0.18±0.11
(2 ). Using these two results
and their measurement of the time delay,
Kundic et al. (1997)
find
). Using these two results
and their measurement of the time delay,
Kundic et al. (1997)
find
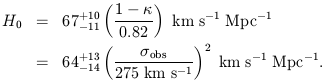
| (4.29)
|
The uncertainty in H0 is quoted at
2 and allows for finite
aperture effects and anisotropy of stellar orbits in conversion of
and allows for finite
aperture effects and anisotropy of stellar orbits in conversion of
 obs to G1 mass
(GN). While this estimate of H0 can
certainly be improved by future observations, it is already 10% accurate
at the 1
obs to G1 mass
(GN). While this estimate of H0 can
certainly be improved by future observations, it is already 10% accurate
at the 1 level.
level.