4.5. The Inflationary Paradigm and = 1

It hass been 30 years since Penzias and Wilson discovered the CMB. This observation is the very foundation of the Hot Big Bang cosmological model. In its early formulation, this model lead to a low density, baryon dominated Universe of age 18 billion years (e.g., Sandage 1982). However, with the evidence presented above about the existence of dark matter, a fundamental alteration of this baryon-dominated cosmological model might be required. In addition, when looked at in detail, the Hot Big Bang model does not naturally predict some aspects of the large scale nature of the Universe. These predictive problems are enumerated below. In an effort to develop a model which more predictive power, a radical new model was proposed fifteen years ago by Alan Guth and colleagues (see Guth 1980). This alteration is known as the inflationary model. In brief, this model postulated the existence of a phase-transition in the earliest moments of the Universe which lead to a brief period in which universal expansion was exponential in nature. This exponential expansion epoch is called "inflation" because, among other things, any initial curvature in the early Universe would be inflated away by the rapid expansion thus producing a spatially flat Universe. Spatial flatness requires the curvature term in the Robertson-Walker metric (K in Chapter 1) to be zero. This in turn requires = 1 and a dark matter dominated Universe. Hence, if inflation indeed is the correct paradigm for the physics of the early Universe, then it makes a fairly definition prediction regarding the mass distribution.

An excellent and detailed overview of the physics of the early Universe under this model is offered in the book The Early Universe by Turner and Kolb. Besides being a possible "natural" result of a phase-transition, inflation also solves three problems that that are not adequately addressed by the standard Big Bang model that has no inflationary epoch. These problems are:

1. The Flatness Problem: Equations 1.23 and 1.28 can be combined to yield

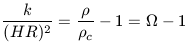
(22a)

Since is time dependent (its decreasing with expansion) then is also time dependent and we an write

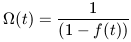
(22b)

where

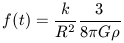
(22c)

At early times was enormous and hence f(t) is very small and is very close to unity and the Universe is spatially flat. This condition is independent of the present epoch value of (₀). The observation that ₀ is in the range 0.01 -1, despite the fact that the scale factor has increased enormously has lead many to suggest that ₀ = 1 or else the Universe would have either re-collapsed long ago or be curvature dominated (radius of curvature the Hubble length) at the present epoch. A specific value of ₀ in the range 0.01-1 would imply that the conditions at the present epoch are somehow imprinted on the initial conditions that determine the expansion.

2. The Horizon Problem: In an expanding universe there are particle horizons. The size of these horizons to first order is set by the speed of light and the expansion rate so that r_hor ~ cT_exp. As the universe ages (expands), the particle horizon increases and more material can come into causal contact with that particle. At early times, individual particle horizons could encompass only a fraction of the volume of the Universe. It can be shown (see the derivation in Kolb and Turner) that the horizon size at any redshift epoch is proportional to the entropy (basically the number of photons) within that horizon volume. For the matter dominated Universe this can be expressed as

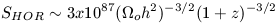
(23)

At the present epoch (z = 0), we have S_HOR 10⁸⁸ (which corresponds to a CMB photon density of about 400 cm^-3). At the time of recombination, z 1000, we have S_HOR 10⁸³ so that the Universe at z = 0 consists of 10⁵ causally disconnected regions. At the time of recombination, the angular size of a particle horizon was 1-2 degrees and yet over 360 degrees of sky, the CMB photon density is the same. Consideration of the observed abundances of light elements only exacerbates this issue. At the time of cosmological nucleosynthesis, S_HOR 10⁶³ yet the observed abundances of light elements today show no variation. Thus, over 10²⁵ causally disconnected regions, the Universe shows homogeneity. This demands that the initial conditions of the Big Bang were homogeneous and that would be a very improbable state.

3. The Smoothness Problem: On a large scale the Universe is extraordinarily smooth, as evidence by the low anisotropy measured by COBE. Yet in this smooth Universe, there exists galaxies which are local density enhancements of order 10⁴. It will be shown in the next chapter that density enhancements ( / ) grow linearly, due to gravitational effects, with scale factor. A natural gravitational timescale is known as the Planck time which is 10^-43 seconds. Galaxy formation commenced when the Universe was 10¹⁵ seconds old and hence, there is potentially a 10⁵⁸ scale in the growth of density fluctuations. If fluctuations are allowed to grow over this scale then the observed structure in the Universe could have formed out of a very initially smooth state. However, in the early Universe purely baryonic density fluctuations are not allowed to be amplified linearly The problem in the early Universe is due to the high radiation pressure of the photon field to which they are coupled. Baryonic density fluctuations can then only grow linearly after recombination at 10⁵ seconds has occurred. In this sense, structure formation is greatly aided if there is some form of matter that is able to "gravitate" but which is not affected by radiation drag. The elegance of the inflationary paradigm lies in its simultaneous solution of these three problems. The root of the paradigm is a brief period in the early Universe where it expanded exponentially instead of linearly. This exponential expansion caused the Universe to increase in scale by a factor of 10⁵⁰. The trigger for this inflationary epoch is a competition in the early Universe between vacuum energy density (which acts as a source of negative pressure) and the kinetic energy density which is essentially an entropy field that currently drives the uniform expansion and cooling of the Universe. It is possible to define a particular form for the scalar field that incorporates a potential energy function, usually expressed as V(). The scalar field, is only weakly coupled to other fields that may be present. If is everywhere the same (e.g., spatially homogeneous) then it is possible to express the energy density and pressure of this fluid to first order as

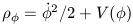
	(24a)
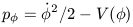
	(24b)

Equation 24 is a partial solution to the stress-energy tensor use to describe the field. In the derivation of these equations, the early Universe is assumed to conform to the Robinson-Walker metric described in chapter 1 and is assumed to obey Einstein's field equations. The term ² / 2 is the kinetic energy density. If V() varies slowly with and if the time derivative of is also small then the early Universe can be characterized by ² / 2 << V. In this case, = -p and the Universe acts exactly as if a Cosmological Constant dominated the stress-energy tensor.

This source of negative pressure causes the Universe to undergo an exponential expansion of its scale factor. Presumably this inflationary epoch must end whenever a condition is achieved such that V() is at a minimum and the potential energy of the field is then converted into kinetic energy density. In practice, V() will oscillate around this minimum. As the scalar field is weakly coupled to other fields, this oscillation will quickly cause the enormous amount of vacuum energy to be dumped into the kinetic energy field which effectively re-heats the Universe and fixes its entropy. After this time, the Universe expands and cools.

The actual physical conditions which determine the turn-on and turn-off phases of inflation remain obscure. Most physicists believe that inflation is like a symmetry breaking phase-transition. The dominance of the vacuum energy field may then be a response to symmetry breaking at the GUTs energy scale. The end of the inflationary epoch is thought to be caused by another phase transition in which the symmetry between the weak nuclear force and the electrostatic force was broken. This occurs at an energy scale of 500 Gev or a time scale of 10^-15 seconds. At this time, the potential has achieved a minimum meaning that the Cosmological Constant has decayed to some minimum value and remained constant since then. This minimum value need not have been zero.

This period of exponential expansion have inflated out any initial curvature and hence inflation directly solves the flatness problem. In particular, inflation predicts a spatially flat Universe (to 1 part in 10⁵⁰). The horizon problem is also directly solved as the initial conditions could have been quite heterogeneous. A tiny region of that heterogeneous mixture (and this tiny region was homogeneous) inflated to produce our observable, homogeneous Universe. Inflation allows for the existence of other inflated Universes which occupy different domains. Theorists enjoy speculating that boundaries between these inflated domains, called domain walls, may have been present in our Universe with observable consequences.

As a consequence of predicting that space must be spatially flat, inflation then demands a Universe which is dark matter dominated. Interestingly, this provides a solution to the smoothness problem. If dark matter dominates the potential of structures which have trapped baryons, then we can allow it to be of a form that does not interact with the radiation field in the early Universe. This allows density fluctuations to begin growing at very early times. Thus, a galaxy size density fluctuation could grow from an initial dark matter density enhancement by a factor of 10³⁰ if we start the growth at the time of electroweak symmetry breaking. A universe at this time which was smooth to one part in 10³⁰ is quite consistent with the CMB observations.

In sum, the inflationary paradigm, while operating via some unknown but clearly fundamental physics, provides some elegant solutions to the problems encountered in the standard big bang model which is baryon-mass dominated. Lately, inflation has come under fire because most observations do not indicate that ₀ = 1, as predicted. However, inflation only predicts a spatially flat Universe and the curvature of the Universe is determined by both and . Hence, if we believe the observations that 1 and that the inflationary paradigm must hold, we are again driven to considerations of a non-zero . In addition, there are some esoteric but opaque "inflationary" models that do predict significant spatial curvature. Since we don't understand those, they are not considered here (but see references in Kolb and Turner).