7.1. Revisting the Questions of Chapter 1
We conclude this treatment of observational cosmology by revisiting the questions that were initially asked in Chapter 1. Throughout this book we have attempted to confront each of those questions with the best available observational data. At the end we will discuss a series of promising new kinds of cosmological observations that can be made with improving instrumentation and telescope aperture. These have the potential to offer even more constraining power on competing cosmological models. For now we assess our cosmological knowledge, as of mid-1997, which is anchored firmly in observations and a realistic assessment of possible systematic errors in them. In evaluating this assessment the reflective reader/student should keep in mind the two themes articulated in Chapter 1: 1) At any given time in history, everyone believes their cosmological models are correct; 2) History shows that cosmological models are subject to great change once better observations become available. In fact, falsification is the scientific history of cosmological model making and our current cosmology will certainly be subject to heavy revision in the years to come. For now we offer the following summary positions, which are consistent with the data, on each of the key questions posed early on:
What is the age of the universe as determined from the observed expansion rate and cosmological distance scale? Is there a need to invoke the cosmological constant to reconcile the ages of the oldest stars with the value of the Hubble constant?
This was the subject of Chapter 2. At two recent meetings on the distance scale, one in 1996 May at the Space Telescope Science Institute and the other in 1996 June at Princeton University, many of participants felt that a convergence on the estimation of H0 had finally occurred. However, this convergence is still a manifestation of overlapping error bars and probably small systematic effects associated with choice of sample. There is still no reason to be particularly optimistic that H0 has been derived to an accuracy of 10%. While it does seem true that the decades old H0 = 50 vs H0 =100 battle has converged to H0 = 60 vs H0 = 85, the entire range remains open given the error bars. The major source of uncertainty in the distance scale continues to be disagreement over distances to nearby galaxies, particularly the LMC. This disagreement notably manifests itself by a significant difference in zeropoint between the Cepheid distance scale and the RR Lyrae distance scale. Probably the most encouraging development in the last few years is the convergence on the distance to the Virgo cluster. Three somewhat independent methods, Cepheids, Surface Brightness Fluctuations, and the Planetary Nebula Luminosity Function all give a consistent distance to Virgo. The consistency of this distance is now even more firmly anchored in the latest Cepheid results from the HST key program (see Graham et al. 1996). However, the distance to Virgo is one step significantly removed from the determination of H0 due to the tremendous difficulty of determining the true cosmic velocity of Virgo. This difficulty is caused both by the structure of the Virgo Cluster itself, and the unknown infall velocity of the Local Group. Using a consistent set of values for infall and the cosmic velocity of Virgo does yield an estimate of H0 which is 80 ± 10, with a possible systematic effect of +10% if the distance to the LMC is (m - M) = 18.35, as suggested by several indicators.
At odds with these estimations is the determination of the extragalactic
distance scale using Supernova Ia as standard candles. After applying
corrections based on the luminosity vs. decline-rate relation, SN Ia
appear to give very good relative distances between galaxies. The
most recent absolute calibration of that data set, based on Cepheid
distances to the calibrators, yields H0 = 65 ± 5
(see Reiss et al. 1996).
However, this does not mean that cosmologists should be
comfortable and now believe that H0 has been pinned
down to occupy
the range 65-80. As Sandage (1996) is quick to point out, there remain
several possible sources of systematic error that can push the data down
to H0 = 50. As this debate is now
35 years old, it seems that
the best resolution will come when distance estimates from more direct
means become available. Very recently, an opportunity has arisen.
In December of 1994, one of the components of the lensed QSO system
0957+061 brightened by 10%. Previous timing observations in the
radio and optical have failed to distinguish between a time delay of
536 days vs 415 days. Analysis of the light curve since the December
94 event by Turner et al. (1996) seems to have resolved this ambiguity
and produce a delay time of
410 days. While there
is still considerable uncertainty in the mass distribution within
the lensing system (see Fischer et al. 1996), a tentative value of
H0
82 can be derived using the
Grogin and Narayan (1996) model of the mass distribution.
Until more such systems are measured, this
value again should be regarded as consistent with other determinations
but in no way is it definitive.
If a consistent extragalactic distance scale can ever be obtained
form observations which indicates the H0 is greater
than 70 and if
we believe that stellar evolutionary theory is sufficiently understood
to yield fairly precise ages for globular cluster stars, then we
have little choice but to appeal to non-zero
as the principal
means of resolving this conflict. Throughout this book we have
presented other lines of observational evidence that favor non-zero
.
In particular if H0 is greater than 70 then all
= 0
CDM structure formation models can be ruled out leaving behind various
non-zero models which have
already been shown to fit the
large scale structure data rather well. Thus both the determination of
the extragalactic distance scale and the measure of the power spectrum
of galaxies on large scales can be made consistent in a
non-zero cosmology. This is
either a coincidence or
observations are telling us something fundamental about the nature of
the Universe.
The major effect of a positive value of
is
that the volume element per unit redshift is significantly higher
than in the = 0 case. In
principle, the space density of
QSO absorption lines (Malhorta and Turner 1996)
and gravitational lens systems are sensitive
probes of the volume per unit redshift (Schneider 1995). At the moment,
the data set
is not sufficiently large to adequately constrain
(but see
Kochanek 1996 for an optimistic counter-argument) leaving
very much open the possibility that the current data is best reconciled
with non-zero . In a possibly
prescient piece of work, Pen (1997)
shows that its not possible to reconcile CDM with both standard Big
Bang nucleosynthesis and the luminosity-temperature relation for
clusters of galaxies. Pen concludes that the luminosity-temperature
relation, in conjunction with the measurment of a possibly low
deuterium abundance by Tytler et al. (1996), greatly favors the
-dominated Universe.
Hence, several lines of observational evidence now suggest non-zero
. As a consequence, models
which now incorporate
are being seriously considered. Indeed, the best evidence of this is the
current plethora of papers which deal specifically with
non-zero models
and/or attempts to either verify it or refute with observations of
gravitational lenses (see among the many -
Klypin et al. 1997; Kashlinsky and Jimenez 1997; Horack et al. 1996;
Mo and Fukugita 1996; Kochanek 1996; Amendola 1996; Lin et al. 1996;
Wu and Shude 1996; Efstathiou 1995; Bunn and Sugiyama 1995;
Malhorta and Turner 1995; Sivaram 1994; Ratra and Peebles 1994;
Peebles 1994).
These models were virtually absent from the literature just a few years
ago. Whether this is just a temporary condition or a manifestation
of real learning will only be discerned when future data is available
to confront these new models. In any event, the
historical comments made in Chapter 1 are
relevant here: Cosmological
models change with time - should future data demonstrate that
is indeed 0 and that H0 is greater than 70, and that
the Universe is at least 15 billion years old, then very little of what
has been presented in this book can be correct.
What is the nature of the large-scale distribution of matter in the universe as traced by the three-dimensional galaxy distribution?
This was the subject of chapter 3. There is no doubt from the observations that the distribution of light (galaxies) is clustered on a variety of size scales (see Bahcall 1996 for recent review). Redshift surveys such as the CFA Slice survey, or the Southern Sky Strip survey have revealed a remarkably complex galaxy distribution. Attempts to push deeper into redshift space have produced power spectra which have features on very large scales. This high degree of clustering makes it very difficult to determine if a fair volume of the Universe has yet been sampled. If light traces the distribution of mass fairly on large scales (another open question), then the high degree of galaxy clustering suggests inhomogeneities in the mass distribution. These will manifest themselves by exerting a gravitational influence on other galaxies (which now are test particles probing the velocity field) causing a deviation from pure expansion velocity. These peculiar velocities which arise from variations in the density field need to be accounted for in any full kinematical description of the local velocity field. As a result, determining H0 from local observations (e.g., the distance to the Virgo Cluster) is severely compromised by uncertainties in our model of the local velocity field. This is why a determination of the distance to Coma, which is a very massive cluster and hence ought to have very little peculiar velocity, is much better for determining H0.
Although we are far from having a complete picture of large scale structure, the following seem fairly well-established:
On small scales both the
galaxy-galaxy correlation length
and the pairwise velocity dispersion are known fairly accurately.
These values are
8 ± 1
h-1 Mpc and 300 ± 100 km s-1
respectively. These values could reflect the conditions of structure
formation or they could be modifications as a result of significant
small scale merging.
There is a definitive
relation between surface brightness
(or morphological type) and local galaxy density. Ellipticals (very
high surface brightness systems) are prevalent in the virialized cores
of clusters while spiral galaxies (and LSB galaxies) occur in regions
of lower galaxy density. This suggests that sparse sampling of spiral
galaxies might be the best tracers of the large scale density field.
Clusters of galaxies
themselves seem to be strongly correlated
(more so than individual galaxies) and form larger superclusters. In turn,
there is some evidence from orientation measures that even superclusters
are correlated. The most intriguing observations in this regard as
that of West (1993) who demonstrates that the major axis of many powerful
radio galaxies in the cores of rich clusters is aligned to that of the
host supercluster. This remarkable observation suggests that structure
formation maintains its memory of initial conditions over many length
scales.
Its clear that we live in a
void filled Universe with the
void filling factor approaching 75%. The characteristic size of a void
is 3500 km/s in diameter and
the larger ones are
6000 km s-1.
The once astounding Bootes void, now appears to be a typical large void
of diameter 5-6000 km s-1 (see Aldering et al. 1997). While
distortions
in redshift space caused by peculiar velocities can render the appearance
of physical structure in redshift surveys, measurements of relative
distances to galaxies on the near and far side of voids (bubbles) indicates
that the voids are very nearly spherical structures which are massless
(see Bothun et al. 1992). The intersections of these spherical voids
produces surfaces which are inhabited by galaxies which give rise to
a filamentary component to the galaxy distribution. The most striking
example of this is the Great Wall (Geller and Huchra 1989), which is now
known also to be a real structure in physical space. Distance measurements
by Dell'Antonio et al. (1996) show that the wall is a cold, thin structure
with little peculiar or shear velocity.
The peculiar velocity field
of the nearby Universe is
complex. While the signature of a dipole moment is unmistakable,
the source of that perturbation remains unidentified. The existence
of quadrapole moments in the nearby velocity field now seem
well established. However, there
is no clear resolution between bulk flow models in which
virialized structures themselves are participating in the flow or
infall models (e.g., the Great Attractor) that are generated by virialized
structures which are at rest. Attempts to infer the large scale density
field from well-defined redshift surveys (e.g., Fisher et al. 1995)
to predict the all sky peculiar velocity vectors have had only
marginal success in matching the observations. The scale over which
the peculiar velocity field converges remains unknown. The Lauer and
Postman (1994) result suggests that volumes with diameters as large
as 15,000 km s-1 have a bulk peculiar velocity of a few 100
km s-1. Such
a flow can not be accounted for in any structure formation model
given the observed degree of anisotropy in the CMB as measured by COBE.
Recent attempts at recovering the LP vector from other data sets
(e.g., Reiss et al. 1996, Giovanelli et al. 1996
Pilonis et al. 1996, Dell'Antonio et al. 1996)
are marginally inconsistent with the original result but can not
rule it out.
Attempts to measure
directly from the peculiar
velocity field have yielded ambiguous results. Sample and scale
dependent results permeate the literature. Moreover, under the linear
biasing model it is only the parameter
|
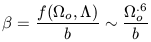
which is measured. In their excellent and comprehensive review of the
current situation, Strauss and Willick (1995) use 24 different methods
to estimate 
. Those
estimates can be characterized by a
quasi-Gaussian distribution with mean 0.75 and dispersion 0.30. It is
thus clear that is
unknown to at least a factor of 2.5.
Furthermore, since the value of b is unknown (although most recent
results suggest b 1), this
introduces more uncertainty into the determination of
0.
Clusters of galaxies are
very ambiguous tracers of
.
On the one hand, the high degree of substructure observed in most
clusters suggests a long formation process and high
as
structure freezes out (e.g., stops growing) roughly at z = 1 /
.
On the other hand, recent observations of the baryonic mass fraction
in clusters strongly argues for
0.3. Clearly,
clusters of galaxies are not a clean laboratory for determinations
of .
What is the evidence for the existence of dark matter and
what is its overall contribution to the total mass density of the
Universe?
This was the subject of Chapter 4 and the
nature of the dark matter (DM)
remains a profound cosmological mystery. The evidence for some
amount of DM , based on galaxy rotation curves, the velocity
dispersion of clusters of galaxies, and gravitational lens systems
is overwhelming and unambiguous. In general, these system have total
M/L ratios which suggest
0.2,
On the other hand, if = 1,
then it is clear that the great
majority of the DM must be non-baryonic. The existence of non-baryonic
gravitating DM may be key to the formation of galaxies in the Universe
as such material will be much less affected by radiation drag in the
early Universe and hence density perturbations can begin to grow at
very early times. Fluctuations in purely baryonic matter are easily
damped out by the radiation when baryonic matter is coupled to the photon
field. The presence of significant amounts of non-baryonic DM means
that an initially very smooth Universe
(which is thought to characterize its early state) can give rise to
structure at later times.
The elegant inflationary
paradigm, which accurately predicts most of the large sale properties
of the Universe, strongly predicts a spatially flat Universe.
For the = 0 case, this means
= 1 and dominance by
non-baryonic matter. Although the inflationary paradigm is deeply
rooted in the (unknown) physics of the very early universe and hence
one is predisposed to favor it as the proper paradigm, there is rather
little observational evidence to support its
= 1 prediction.
Thus spatial flatness is either achieved through some combination
of and
, or the paradigm is
incorrect, or the Universe
is still more complex than standard inflation can account for. Clearly
we will be unable to distinguish between these possibilities until we
actually know what the DM is. While the list of candidates
appears to grow each year, the current status can be summarized as follows:
Baryonic DM:
The constraints on the total baryonic content of the Universe
from considerations of primordial nucleysynthesis and the observed
abundances of light elements are fairly severe. At most, they allow
b to be
0.1. However, since the luminous parts of galaxies
only contribute 0.005 to
, we know that baryonic DM must
exist and is most likely in the form of low mass stars or stellar
these remnants in normal galaxies and a significant population of
LSB galaxies. Direct searches for baryonic DM are now underway and the
microlensing experiments towards the LMC and the Galactic Bulge have
produced a significant number of events. The line of sight toward the
LMC is more sensitive to halo baryonic DM and to
date, a total of 8
events have been detected by the MACHO project. While analysis of
these events is still ongoing, the distribution of lensing masses is
consistent with a population of low mass main sequences stars and/or
white dwarfs. Filling the halo up with Jupiter mass objects can be
ruled out. The total amount of baryonic DM in the halo inferred from
these lensing events is consistent with that inferred from the rotation
curve of the Galaxy and observations of satellite companion galaxies
to bright spiral hosts whose relative velocities suggest total halo
masses of 1-2 x 1012
M
and radial extents of
200 kpc (Zaritsky et al. 1996).
CDM: While CDM remains the
preferred theory for structure
formation (due to the intrinsic shape of the CDM power spectrum)
there still is no identifiable CDM particle but there are
a plethora of candidates. Supersymmetric theory in combination with
R-parity conservation predicts that a stable particle must exist and
this is the best hope for the CDM particle. Candidate particles come
and go each year in the particle physics world and it becomes a
matter of picking the favorite "ino" (e.g., neutralino, higgsino,
photino, etc). The search for these particles is ongoing in
terrestrial accelerators and ultimately the fundamental nature of
the DM, and hence our cosmology, may be found at the end of a beam
pipe instead of a telescope.
HDM: At least HDM has a
known particle which may have a
mass, the neutrino. Furthermore, its cosmological density is
known. A plausible resolution to the observed deficit
of solar neutrinos appeals to oscillations between muon and electron
neutrinos as each has a small mass. Positive combined neutrino
masses in the range of 1-10 eV have high cosmological significance
as they would supply much of the observed power on large scales.
A neutrino dominated Universe, however, is ruled out by the observation
that the ages of the galaxies are approximately
H0-1.
How did structure form in the Universe and what formation scenarios are consistent with the current observational data?
This was the subject of Chapter 5. A quick
summary is trivial: we
don't have a structure formation scenario that works. More definitively,
no single structure formation scenario can satisfy the simultaneous
large and small scale constraints. The traditional CDM,
= 1
model over-produces small scale structure when normalized to the COBE
data. Purely baryonic fluctuations (the PBI model) don't appear
likely as 1) they require
b to be in excess of
the primordial
nucleosynthesis constraint and 2) are inconsistent with the (admittedly
uncertain) degree
scale anisotropy observed in the CMB. To
suppress the production of small scale structure, CDM must be augmented
in a manner that essentially extends the time it takes for matter
and radiation to equilibrate. This can be accomplished by lowering
the overall matter density (low H0), increasing the
radiation density
by adding extra relativistic particles, tilting the primordial
spectrum to suppress small scale fluctuations, adding gravity waves
as a source of the observed CBR anisotropy, giving neutrinos a small
mass (the MDM model), or having
dominate over
in
establishing spatial flatness.
Each of these adjustments to the standard CDM theory is somewhat exotic
and renders structure formation all the more complex. Many of these
augmentations are nearly ruled out via observations of H0 and
the highly Gaussian nature of the CMB fluctuations. Given this,
it seems highly significant that the convergence of individuals investigators
characterization of the power spectrum of galaxies strongly favors
either open Universe or non-zero
models. Finally, although
the gravitational instability paradigm remains key, the overall topology
of the Universe strongly suggests that feedback (from explosions?) and
other non-gravitational forces have played a role in structure formation.
This has lead to the incorporation of hydrodynamics into N-body simulations
with often spectacular results (see animations on the Web page).
Now, if we could
only understand the role that magnetic fields play in collapsing
structures we would have all the input physics necessary to construct
a more rigorous set of models. As a consequence of this, models of
galaxy formation are necessarily incomplete.
Where do the baryons reside? Are they predominately inside or outside of galaxies? How efficient was the process of galaxy formation? What is the true nature of the galaxy population? Do we have a representative survey of galaxies in the nearby universe from which coherent arguments about galaxy formation and evolution can be made?
This was the subject of Chapter 6. In general, the various extragalactic backgrounds (aside from the CMB) that have been discovered can be well-explained as due an aggregate discrete source population. There is very little evidence for a diffuse intergalactic medium and certainly no evidence that most of the baryons are in the IGM. The nature of the IGM itself and the evolution of its ionization state with redshift is strongly constrained by the density and ionization states of various QSO absorption line systems. At high redshift, it is probable that these pressure-confined IGM clouds, which won't rapidly collapse to form galaxies, contain much of the baryonic material (see Weinberg et al. 1997). The evolution of these clouds is not well know but they could cool to form dwarf galaxies at some later epoch. Thus baryons seem to be strongly confined to galactic-size potential wells which argues that the capture of baryonic gas by these potentials was fairly efficient. Despite this efficiency we have never actually observed a galaxy that is in the process of formation despite many dedicated searches (Thompson et al. 1995; Pahre and Djorgovski 1995). This implies that either galaxy formation is hidden from us (i.e., its masked by the presence of QSO activity or early star formation is shrouded in dust - Silk and Wyse 1996) or that the bulk of stars in even spheroid dominated galaxies form on a timescale much longer than the dynamical timescale of the system. The morphology of galaxies in the Hubble Deep Field (see Figure 5-3) has been used as evidence that galaxy formation is an extended process that involves assembling and acreting sub-galaxy size regions (see Windhorst et al. 1996).
At much lower redshift, the recent discovery of LSB galaxies and their now inferred large space density is a strong indication that surface brightness selection effects have been severe and quite effective at preventing a representative sample of z = 0 galaxies to be obtained. We thus have predominately observed only one mode of galaxy evolution, that which leads to a conspicuous, HSB object. If figure 6-12 is an accurate representation, however, then we know that we are now only beginning the kinds of observations that will lead to the construction of a representative sample of galaxies. Thus great caution must be exercised when trying to compare the properties and space density of galaxies at modest and distant redshifts to that nearby. As is often the case in extragalactic astronomy, we seem to have more knowledge about distant samples of galaxies than nearby samples. The discovery of LSB galaxies has significantly increased the baryonic census of the nearby Universe (bringing it better into accord with the primordial nucleosynthesis constraints) and has fundamentally altered the faint end slope of the Galaxy Luminosity Function. These galaxies have also given us a window into a different avenue of galaxy evolution which was closed to us for many years due to the failure to detect these diffuse objects.