Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
Astronomy and physics bring different perspectives to the
``cosmological constant problem.'' Originally introduced by Einstein as
a new term in his gravitational field equations [and later regretted
by him as ``the biggest blunder of my life'' (quoted in
Gamow 1970)],
the cosmological constant,  ,
confronts observational astronomers as a
possible additional term in the equation that, according to general
relativity, governs the expansion factor of the universe R(t),
,
confronts observational astronomers as a
possible additional term in the equation that, according to general
relativity, governs the expansion factor of the universe R(t),
Here
Equation 1 says that three competing terms drive the universal
expansion: a matter term, a cosmological constant term, and a
curvature term. It is convenient to assign symbols to their respective
fractional contributions at the present epoch. We define
where zero subscripts refer to the present epoch. Equation 1 then
implies
it is also sometimes convenient to define
The Heisenberg uncertainty principle allows particle-antiparticle
pairs spontaneously to appear and disappear. The theoretical particle
physicist thus sees the
In this review, we sample both the astronomer's and the physicist's
viewpoints. The differing perspectives lead to different perceived
goals. An epochal astronomical discovery would be to establish by
convincing observation that
Attempts to measure fundamental cosmological parameters have
consumed enormous observational (and intellectual) resources but have
met with only limited success (see
Sandage 1987
for a historical
review). Hubble's constant H0 is physically the most
fundamental such
parameter, yet independent determinations via classical techniques
(see reviews by
Tammann 1987 and
de Vaucouleurs 1981)
or the latest new methods
(Tonry 1991,
Roberts et al 1991,
Press et al 1991,
Birkinshaw et al 1991,
Jacoby et al 1990,
Aaronson et al 1989)
give values that vary over a factor of two. Attempts to measure the value
of
In comparison with H0 and
Table 1 lists five fiducial cosmological models,
parametrized by
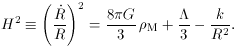
 M is
the mass density; k = - 1, 0, + 1 for a Universe that is
respectively open, ``flat,'' and closed; and H is the Hubble constant,
whose observable value at the present epoch t0 is
denoted H0.
M is
the mass density; k = - 1, 0, + 1 for a Universe that is
respectively open, ``flat,'' and closed; and H is the Hubble constant,
whose observable value at the present epoch t0 is
denoted H0.
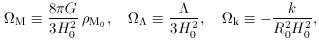
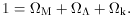
 tot =
tot =
 M +
M +

 = 1 -
= 1 -
 k. It is
an observational question whether a non-zero
k. It is
an observational question whether a non-zero

 is required to achieve
consistency in Equation 3. This is the astronomer's cosmological
constant problem.
is required to achieve
consistency in Equation 3. This is the astronomer's cosmological
constant problem.

 term
in Equation 3 as an inevitable
concomitant to the
term
in Equation 3 as an inevitable
concomitant to the  M
term. As
M
term. As  M is
associated with a density of real
particles, so
M is
associated with a density of real
particles, so 
 is associated with virtual,
``vacuum'' states of those
same particles' species - that is, with the energy-momentum density of
their vacuum states. The gravitational effect of these virtual
particles gives the vacuum an energy density
is associated with virtual,
``vacuum'' states of those
same particles' species - that is, with the energy-momentum density of
their vacuum states. The gravitational effect of these virtual
particles gives the vacuum an energy density
 vac
(Zel'dovich 1967).
Although particle physicists do not know how to compute
vac
(Zel'dovich 1967).
Although particle physicists do not know how to compute
 vac exactly,
theory allows one to estimate its value. Unfortunately, the estimates
disagree with observational limits by a factor of 10120. This is the
physicist's cosmological constant problem.
vac exactly,
theory allows one to estimate its value. Unfortunately, the estimates
disagree with observational limits by a factor of 10120. This is the
physicist's cosmological constant problem.
 is non-zero. An important physics
discovery, on the other hand, would be to adduce a convincing
theoretical model that requires
is non-zero. An important physics
discovery, on the other hand, would be to adduce a convincing
theoretical model that requires
 to be exactly zero.
to be exactly zero.
 M have been even
less conclusive (see reviews by
Peebles 1986,
Trimble 1987,
Fukugita 1991).
New results supporting apparently inconsistent values continue to appear (e.g.
Toth & Ostriker 1992,
Richstone et al
1992).
M have been even
less conclusive (see reviews by
Peebles 1986,
Trimble 1987,
Fukugita 1991).
New results supporting apparently inconsistent values continue to appear (e.g.
Toth & Ostriker 1992,
Richstone et al
1992).
 M, attempts to
measure
M, attempts to
measure 
 have been
infrequent and modest in scope. Moreover, in many respects, the
physical signatures of
have been
infrequent and modest in scope. Moreover, in many respects, the
physical signatures of 
 are
smaller and more subtle than those of
the other two parameters, at least from an observational
perspective. These considerations should severely limit our
expectations for current observational information concerning
are
smaller and more subtle than those of
the other two parameters, at least from an observational
perspective. These considerations should severely limit our
expectations for current observational information concerning

 .
.
 M
and
M
and 
 , which we will refer to in
following sections as Models A
through E. They represent extreme, though not impossible, limits on
the present state of knowledge. In fact, we will see that
distinguishing among these models, and thus among variations in
Equation 3 having dominant versus negligible
, which we will refer to in
following sections as Models A
through E. They represent extreme, though not impossible, limits on
the present state of knowledge. In fact, we will see that
distinguishing among these models, and thus among variations in
Equation 3 having dominant versus negligible

 terms, is quite
challenging at present.
terms, is quite
challenging at present.
Model
 tot
tot
 M
M


Description
A 1 1 0 flat, matter dominated, no

B 0.1 0.1 0 open, plausible matter, no

C 1 0.1 0.9 flat,
 plus plausible matter
plus plausible matter
D 0.01 0.01 0 open, minimal matter, no

E 1 0.01 0.99 flat,
 plus minimal matter
plus minimal matter