Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
In this section we discuss the form that the vacuum energy-momentum
tensor must take, and why the predicted value of
 vac is
unreasonably high
(Weinberg 1989;
for nontechnical introductions see
Abbott 1988
and Freedman 1990).
vac is
unreasonably high
(Weinberg 1989;
for nontechnical introductions see
Abbott 1988
and Freedman 1990).
To a particle physicist, the word ``vacuum'' has a different meaning
than to an astronomer. Rather than denoting ``empty space,'' vacuum is
used to mean the ground state (state of lowest energy) of a theory. In
general, this ground state must be Lorentz invariant, that is, must
look the same to all observers. If this is the case, then the
stress-energy- momentum tensor Fµv of vacuum must be
proportional (in
any locally inertial frame) simply to the diagonal Minkowski metric,
diag(-1, 1, 1, 1), because this is the only 4 x 4 matrix that is
invariant
under Lorentz boosts in special relativity (as can easily be checked).
As is well known, a perfect fluid with density
 and pressure P has
the stress-energy-momentum tensor
diag(
and pressure P has
the stress-energy-momentum tensor
diag( , P, P,
P). (see, e.g.
Misner et al. 1973;
in this section, we choose units with c = 1). Comparing to
the Minkowski metric, it follows that (a) ``vacuum'' is a perfect fluid,
and (b) it has the equation of state
, P, P,
P). (see, e.g.
Misner et al. 1973;
in this section, we choose units with c = 1). Comparing to
the Minkowski metric, it follows that (a) ``vacuum'' is a perfect fluid,
and (b) it has the equation of state
Not by coincidence, this equation of state is precisely the one that,
under application of the first law of thermodynamics, causes
In nongravitational physics, the energy of the vacuum is irrelevant.
In nongravitational classical mechanics, for example, we speak of
particles with energy E = T + V, where T is
the kinetic energy and V
the potential energy. The force on a particle is given by the gradient
of V; therefore, we may add an arbitrary constant to V without
affecting its motion. Often we choose this arbitrary constant so that
the minimum of V is zero, and we say that the particle has zero energy
in its vacuum state.
In quantum mechanics the situation is more complicated. Consider,
for example, a simple harmonic oscillator of frequency
The generalization of this phenomenon to quantum field theory is
straightforward
(Feynman & Hibbs 1965,
Mandl & Shaw 1984).
A relativistic field may be thought of as a collection of harmonic
oscillators of all possible frequencies. A simple example is provided
by a scalar field
where the sum is over all possible modes of the field, i.e. over all
wavevectors k. We can do the sum by putting the system in a box of
volume L3, and letting L go to infinity. If we
impose periodic
boundary conditions, forcing the wavelength (in, say, the ith
direction) to be
The energy density
As we let the cutoff kmax approach infinity,
This, as we will see later, is approximately 120 orders of magnitude
larger than is allowed by observation.
We might boldly ignore a discrepancy this large, if it were not for
gravity. As in classical mechanics, the absolute value of the vacuum
energy has no measurable effect in (nongravitational) quantum field
theory. However, one of the postulates of general relativity is that
gravitation couples universally to all energy and momentum; this must
include the energy of the vacuum. Since gravity is the only force for
which this is true, the only manifestation of vacuum energy will be
through its gravitational influence. For a density as high as given by
Equation 8, this manifestation is dramatic: if
One may object that we have simply chosen an unrealistically high
value for kmax. However, to satisfy cosmologically observed
constraints, we would need kmax < 10-3
cm-1; in other words, we must
neglect effects at energies higher than 10-14 erg
One can postulate an additional ``bare'' cosmological constant,
opposite in sign and exactly equal in magnitude to
8
We should finally note that possible solutions to the cosmological
constant problem are particularly constrained if they are to be
compatible with the inflationary universe scenario
(Guth 1981,
Linde 1982,
Albrecht &
Steinhardt 1982;
recent reviews are by
Narlikar &
Padmanabhan 1991,
Linde 1990, and
Kolb & Turner 1990).
Inflationary cosmology postulates an early, exponential expansion driven by the
vacuum energy density of a scalar field trapped in a ``false vacuum,''
away from the true minimum of its potential. During the exponential
phase, this vacuum energy density is, in fact, a non-zero (and quite
large) cosmological constant. Thus, to be compatible with inflation,
whatever physical process enforces
For physicists, then, the cosmological constant problem is this:
There are independent contributions to the vacuum energy density from
the virtual fluctuations of each field, from the potential energy of
each field, and possibly from a bare cosmological constant
itself. Each of these contributions should be much larger than the
observational bound; yet, in the real world, they seem to combine to
be zero to an uncanny degree of accuracy. Most particle theorists take
this situation as an indication that new, unknown physics must play a
decisive role. The quest to solve this puzzle has led to a number of
intriguing speculations, some of which we will review in
Section 5.
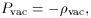
 vac to
remain constant if a volume of vacuum is adiabatically compressed or
expanded: PdV work provides exactly the amount of mass-energy to fill
the new volume dV to the same density
vac to
remain constant if a volume of vacuum is adiabatically compressed or
expanded: PdV work provides exactly the amount of mass-energy to fill
the new volume dV to the same density
 vac. Thus
vac. Thus
 vac
remains truly a constant. Its relation to
vac
remains truly a constant. Its relation to
 is simply
is simply
 = 8
= 8 G
G
 vac.
vac.
 ; that is, a
particle of mass m moving in a one dimensional potential well
V(x) =
1/2 m
; that is, a
particle of mass m moving in a one dimensional potential well
V(x) =
1/2 m 2
x2. We have chosen the potential such that it has a
minimum V(0) =
0. However, the uncertainty principle forbids us from isolating the
particle in a state with zero kinetic energy and zero potential energy (of
Cohen-Tannoudji et
al 1977).
In fact, the vacuum state has a
zero-point energy E0 =
1/2
2
x2. We have chosen the potential such that it has a
minimum V(0) =
0. However, the uncertainty principle forbids us from isolating the
particle in a state with zero kinetic energy and zero potential energy (of
Cohen-Tannoudji et
al 1977).
In fact, the vacuum state has a
zero-point energy E0 =
1/2 
 . Note that we could have set this energy to
zero, simply by subtracting 1/2
. Note that we could have set this energy to
zero, simply by subtracting 1/2

 from the definition of the potential;
quantum mechanics does not restrict our freedom to pick the zero point
of energy. However, it does imply that the energy of a vacuum state
will differ from our classical expectation, and that the difference
will depend on the physical system (in this case it is a function of
from the definition of the potential;
quantum mechanics does not restrict our freedom to pick the zero point
of energy. However, it does imply that the energy of a vacuum state
will differ from our classical expectation, and that the difference
will depend on the physical system (in this case it is a function of
 ).
).
 (i.e. a spinless
boson) of mass m. For this
system, the vacuum energy is simply a sum of contributions
(i.e. a spinless
boson) of mass m. For this
system, the vacuum energy is simply a sum of contributions
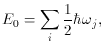
 i = L /
ni for some integer ni, then, since
ki =
2
i = L /
ni for some integer ni, then, since
ki =
2 /
/
 i, there
are dkiL / 2
i, there
are dkiL / 2 discrete values of ki in the range
(ki, ki +
dki). Therefore expression 5 becomes
discrete values of ki in the range
(ki, ki +
dki). Therefore expression 5 becomes
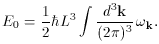
 vac is obtained by letting L ->
vac is obtained by letting L ->
 while
simultaneously dividing both sides by the volume
L3. To perform the
integral, we must use
while
simultaneously dividing both sides by the volume
L3. To perform the
integral, we must use  k2 = k2 +
m2 /
k2 = k2 +
m2 /  2, and
impose a cutoff at a
maximum wavevector kmax >> m /
2, and
impose a cutoff at a
maximum wavevector kmax >> m /
 . Then the integral gives
. Then the integral gives
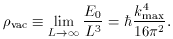
 vac
becomes divergent.
In the venerable rhetoric of quantum field theory, this is known as an
``ultraviolet divergence,'' since it comes about due to the contribution
from modes with very high k. Such divergences are only modestly
worrisome. We know that no simple low-energy theory is likely to be
exactly true at high energies, where other particles, and possibly new
kinds of forces, become important. Therefore, we can estimate
kmax as
the energy scale at which our confidence in the formalism no longer
holds. For example, it is widely believed that the Planck energy
E*
vac
becomes divergent.
In the venerable rhetoric of quantum field theory, this is known as an
``ultraviolet divergence,'' since it comes about due to the contribution
from modes with very high k. Such divergences are only modestly
worrisome. We know that no simple low-energy theory is likely to be
exactly true at high energies, where other particles, and possibly new
kinds of forces, become important. Therefore, we can estimate
kmax as
the energy scale at which our confidence in the formalism no longer
holds. For example, it is widely believed that the Planck energy
E*  1019 GeV
1019 GeV  1016 erg marks a point where conventional field theory
breaks down due to quantum gravitational effects. Choosing
kmax = E* /
1016 erg marks a point where conventional field theory
breaks down due to quantum gravitational effects. Choosing
kmax = E* /
 , we obtain
, we obtain
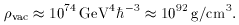
 vac =
1092 g/cm3, the
cosmic microwave background would have cooled below 3 K in the first
10-41 s after the Big Bang.
vac =
1092 g/cm3, the
cosmic microwave background would have cooled below 3 K in the first
10-41 s after the Big Bang.
 10-2 eV. This is not
very high at all; the binding energy of the electron in a hydrogen
atom is much larger, and is experimentally tested to very high
precision. Moreover, there is direct experimental evidence for the
reality of a vacuum energy density in the
Casimir (1948)
effect: The
vacuum energy between two parallel plate conductors depends on the
separation between the plates. This leads to a force between the
plates, experimentally measured by Sparnaay
(1957; also
Tabor & Winterton
1969),
who found agreement with Casimir's prediction.
Fulling (1989),
in a lucid discussion of the Casimir
effect, notes that ``No worker in the field of overlap of quantum
theory and general relativity can fail to point this fact out in tones
of awe and reverence.''
10-2 eV. This is not
very high at all; the binding energy of the electron in a hydrogen
atom is much larger, and is experimentally tested to very high
precision. Moreover, there is direct experimental evidence for the
reality of a vacuum energy density in the
Casimir (1948)
effect: The
vacuum energy between two parallel plate conductors depends on the
separation between the plates. This leads to a force between the
plates, experimentally measured by Sparnaay
(1957; also
Tabor & Winterton
1969),
who found agreement with Casimir's prediction.
Fulling (1989),
in a lucid discussion of the Casimir
effect, notes that ``No worker in the field of overlap of quantum
theory and general relativity can fail to point this fact out in tones
of awe and reverence.''
 G
G
 vac, so that
the ``net'' cosmological constant is exactly zero. However, the vacuum
energy of quantum field theory does not simply result from the
fluctuations of a single scalar field. In the real world there are
many different particles, each with its own somewhat different
contribution, and with additional contributions derived from their
interactions. Given the large number of elementary fields in the
standard model of particle physics, it is most unlikely that they
conspire to produce a vanishing vacuum energy.
vac, so that
the ``net'' cosmological constant is exactly zero. However, the vacuum
energy of quantum field theory does not simply result from the
fluctuations of a single scalar field. In the real world there are
many different particles, each with its own somewhat different
contribution, and with additional contributions derived from their
interactions. Given the large number of elementary fields in the
standard model of particle physics, it is most unlikely that they
conspire to produce a vanishing vacuum energy.
 = 0 today must also allow it to
have had a large value in the past.
= 0 today must also allow it to
have had a large value in the past.