Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
3.2 The Age of the Universe
By a trivial change of variables in Equation 9, from a to
z and from  to t, we obtain an integral that relates redshift
z1 to lookback time from the present,
to t, we obtain an integral that relates redshift
z1 to lookback time from the present,
This integral can be solved analytically in some special cases, e.g.
when
The integral in Equation 16 goes to a finite limit, the age of the
universe, as z1 ->
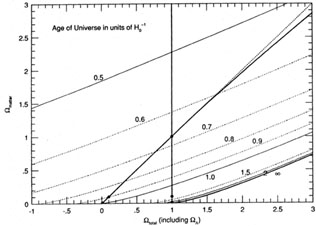
Figure 4. Contours of the age of the
universe are shown in the
Because the contours in Figure 4 are not too
different from lines of
constant slope, one can readily write a simple approximation that is
valid to within a few percent in the range 0 <
where
and ``sinn-1'' is defined as sinh-1 if
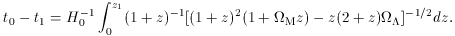

 = 0
(Kolb & Turner 1990,
equations 3.22-3.25;
Sandage 1961a)
or when
= 0
(Kolb & Turner 1990,
equations 3.22-3.25;
Sandage 1961a)
or when  tot = 1
(Weinberg 1989).
In general, it can be calculated
numerically without difficulty. By inspection of the integrand, one
sees that at fixed
tot = 1
(Weinberg 1989).
In general, it can be calculated
numerically without difficulty. By inspection of the integrand, one
sees that at fixed
 M, increasing
M, increasing

 lengthens the lookback time to
any redshift. Eliminating
lengthens the lookback time to
any redshift. Eliminating 
 in
favor of
in
favor of  tot, one
likewise finds that
at fixed
tot, one
likewise finds that
at fixed  tot, the
lookback time to any z lengthens for decreasing
tot, the
lookback time to any z lengthens for decreasing
 M.
Figure 3 shows the lookback time as a
function of redshift for the five models A-E.
M.
Figure 3 shows the lookback time as a
function of redshift for the five models A-E.
 .
Kolb & Turner (1990)
give analytic formulas for
the special cases
.
Kolb & Turner (1990)
give analytic formulas for
the special cases 
 = 0 and
= 0 and
 tot = 1 (see also
Sandage 1961a).
Figure 4
shows the results of numerical integration for general cases with
tot = 1 (see also
Sandage 1961a).
Figure 4
shows the results of numerical integration for general cases with

 ,
,
 tot in the same
range that was shown in
Figure 1. One sees that if
tot in the same
range that was shown in
Figure 1. One sees that if
 M,
M,
 is bounded to a plausible range, then the age of the universe is
between about 0.5 and 2 Hubble times. In
Section 4.2 we will compare
these ages to observational constraints.
is bounded to a plausible range, then the age of the universe is
between about 0.5 and 2 Hubble times. In
Section 4.2 we will compare
these ages to observational constraints.
 M,
M,
 tot)
plane. Away from the infinity line, the contours are close to straight
lines, and Equation 17 is a good analytic approximation.
tot)
plane. Away from the infinity line, the contours are close to straight
lines, and Equation 17 is a good analytic approximation.
 M
M
 1, 0 <
1, 0 <
 tot
tot
 1,and
serviceable anywhere away from the loitering line;
1,and
serviceable anywhere away from the loitering line;
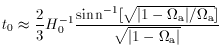
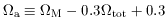
 a
a
 1 (the usual case) and as
sin-1 if
1 (the usual case) and as
sin-1 if
 a > 1. (In fact,
Equation 17 is the exact result when
a > 1. (In fact,
Equation 17 is the exact result when
 tot = 1.)
tot = 1.)