Annu. Rev. Astron. Astrophys. 1992. 30: 499-542 Copyright © 1992 by Annual Reviews. All rights reserved

3.6 Gravitational Lens Probabilities

One effect of a non-zero cosmological constant is to change, in some cases drastically, the probability that quasars are gravitationally lensed by intervening galaxies (Fukugita et al 1990a, Turner 1990). While the absolute lens probability obviously depends on the absolute density and gravitational potential of the lensing galaxies, a useful statistic is the probability for lensing by a population of isothermal spheres of constant comoving density relative to the fiducial case _M = 1, = 0, given by the integral

33.

(Fukugita et al 1992). Here z_s is the redshift of the source (quasar). The prefactor normalizes the fiducial value to unity. The function d(z₁, z₂) is the angular diameter distance from redshift z₁ to redshift z₂, given by the generalization of Equation 25,

34.

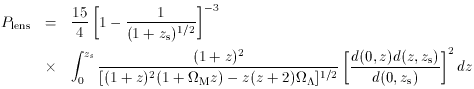
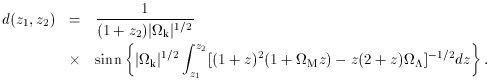
Equation 33 quantifies the geometrical differences affecting ray paths and volumetric factors among different _M and models. Figure 9 plots the value of P_lens in the (_M, _tot) plane for the specific (but reasonable) choice z_s = 2. Along the diagonal line = 0, one sees that lens probabilities increase as the universe becomes emptier, but only by a modest factor ~ 2. By contrast, as the matter density is decreased along the line _tot = 1 (that is, compensated by increasing ), the lens probability rises dramatically, by a factor ~ 10. We will see below that gravitational lensing, because it distinguishes so sharply between low _M universes of differing , holds great promise for putting firm limits on .

Figure 9. Probability for observing a gravitational lens, as contours in the (M, tot) plane, normalized to unity for the case M = 1, = 0. Gravitational lens statistics are the most promising method for ruling out -dominated models along the tot = 1 line, and already give the best bounds on to the right of that line.