Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
3.5 Growth of Linear Perturbations
In all the homogeneous and isotropic cosmologies, linear cold matter
perturbations 


 /
/ grow at a rate that does
not depend on their comoving spatial scale (e.g.
Peebles 1980).
An explicit expression for the amplitude of a growing perturbation
(Heath 1977) is
grow at a rate that does
not depend on their comoving spatial scale (e.g.
Peebles 1980).
An explicit expression for the amplitude of a growing perturbation
(Heath 1977) is
where a' is the dummy integration variable, and da /
d
Different values of
(The remarkable approximation formula - good to a few percent in
regions of plausible
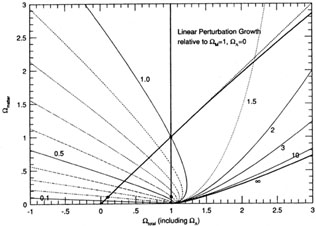
Figure 7. Growth factor for linear
perturbations, as contours in the
(
To the right of the line
Related to the growth of linear perturbations is the relation
between peculiar velocity v and peculiar acceleration g, or (as a
special case) the radial infall velocity vrad around a
spherical perturbation of radius
the relation being
where <
Figure 8 plots f(z) for our standard
models A-E. One sees that, at
small redshifts, peculiar velocities depend almost entirely on
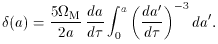
 is to be viewed
as a known function of a or a', in our case given explicitly by
Equation 9. Equation 28 is normalized so that the fiducial case of
is to be viewed
as a known function of a or a', in our case given explicitly by
Equation 9. Equation 28 is normalized so that the fiducial case of
 M
= 1,
M
= 1, 
 = 0 gives the familiar
scaling
= 0 gives the familiar
scaling  (a) = a,
with coefficient unity.
(a) = a,
with coefficient unity.
 M,
M,

 lead to different linear
growth factors
from early times (a
lead to different linear
growth factors
from early times (a  0) to the present (a = 1, da /
d
0) to the present (a = 1, da /
d = 1). Denoting
the ratio of the current linear amplitude to the fiducial case by
= 1). Denoting
the ratio of the current linear amplitude to the fiducial case by
 0(
0( M,
M, 
 ) we have
) we have
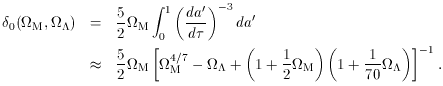
 M,
M,

 - follows from
Lahav et al 1991 and
Lightman &
Schechter 1990.)
Figure 7 shows
numerical values for
- follows from
Lahav et al 1991 and
Lightman &
Schechter 1990.)
Figure 7 shows
numerical values for  0
(
0
( M,
M,

 ) for the region in the
(
) for the region in the
(
 ,
,
 tot)
plane previously seen in Figures 1
and 4. One sees that as
tot)
plane previously seen in Figures 1
and 4. One sees that as
 M is reduced from
unity, both along the line
M is reduced from
unity, both along the line

 = 0 and along the line
= 0 and along the line
 tot
= 1, the growth of perturbations is
suppressed, but somewhat less suppressed in the
tot
= 1, the growth of perturbations is
suppressed, but somewhat less suppressed in the
 tot = 1 case. The
reason is that, for fixed
tot = 1 case. The
reason is that, for fixed
 M, linear growth
effectively stopped at a
redshift (1 + z) =
M, linear growth
effectively stopped at a
redshift (1 + z) =  M-1 in the open case (when the
universe became
curvature dominated), but, more recently, at (1 + z) =
M-1 in the open case (when the
universe became
curvature dominated), but, more recently, at (1 + z) =
 M-1/3 in
the flat case (when the universe became
M-1/3 in
the flat case (when the universe became
 dominated).
dominated).
 M,
M,
 tot) plane,
normalized to unity for the case
tot) plane,
normalized to unity for the case
 M = 1,
M = 1,

 = 0. There
is relatively less suppression of growth as
= 0. There
is relatively less suppression of growth as
 M is decreased along the
line
M is decreased along the
line  tot = 1 than
along the line
tot = 1 than
along the line 
 = 0; but for credible
values of
= 0; but for credible
values of  M
the difference is not a large factor. Perturbation growth approaches
M
the difference is not a large factor. Perturbation growth approaches
 at the ``loiter line,'' but for credible
at the ``loiter line,'' but for credible
 M it occurs at too small a
redshift to explain quasars (see
Figure 1).
M it occurs at too small a
redshift to explain quasars (see
Figure 1).
 tot = 1 in
Figure 7, one sees values of
tot = 1 in
Figure 7, one sees values of
 0
(
0
( M,
M,

 ) that are greater than 1,
in fact approaching infinity at the loitering cosmology line (cf
Figure 1 and discussion
above). Loitering cosmologies allow the arbitrarily large growth of
linear perturbations, since the perturbations continue to grow during
the (arbitrarily long) loiter time.
) that are greater than 1,
in fact approaching infinity at the loitering cosmology line (cf
Figure 1 and discussion
above). Loitering cosmologies allow the arbitrarily large growth of
linear perturbations, since the perturbations continue to grow during
the (arbitrarily long) loiter time.
 . These quantities
depend not directly on
Equation 28, but on its logarithmic derivative, the exponent in the
momentary power law relating
. These quantities
depend not directly on
Equation 28, but on its logarithmic derivative, the exponent in the
momentary power law relating  to a,
to a,
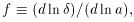
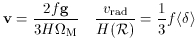
 > is the overdensity
averaged over the interior of the sphere
of radius
> is the overdensity
averaged over the interior of the sphere
of radius  (Peebles 1980,
Section 14). One can calculate
(Peebles 1980,
Section 14). One can calculate 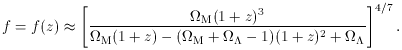
 M and
are quite insensitive to
M and
are quite insensitive to 
 . This
is because they are driven by the
matter perturbations in primarily the most recent Hubble time. Looking
back to redshifts z
. This
is because they are driven by the
matter perturbations in primarily the most recent Hubble time. Looking
back to redshifts z
 1, however, the peculiar
velocities do start
depending on
1, however, the peculiar
velocities do start
depending on 
 , allowing in principle for
observational tests (but see
Lahav et al 1991
for caveats).
, allowing in principle for
observational tests (but see
Lahav et al 1991
for caveats).