


It should, by now, go without saying that the removal of reddening is essential to any study that aspires to a calibration of the intrinsic PLC relation for Cepheids. What is all too often forgotten in the process is that the systematics of this first step will not only affect the calibration, they may well predetermine it. Some authors have claimed that color-color plots for Cepheids can be accurately calibrated and confidently used to determine reddenings to Galactic and extragalactic Cepheids. We examine in some detail now one such case, that of Feast and his collaborators (hereafter referred to as the South African Group). Their calibration is as widespread as its implications, and therefore we discuss it in some detail.
The South African calibration of the reddening determination begins with Galactic Cepheids (Dean et al. (1978). It has then been applied to Magellanic Cloud Cepheids (Martin et al. 1979), where they derive a form of the PLC. And then they have further generalized the dereddening procedure for all extragalactic Cepheids of arbitrary metal abundance (Caldwell & Coulson 1985). Beginning with the specific case of the Galactic calibration the South African Group accept at least four crucial assumptions. Assumption (1): There exists a relation between (B-V) 0 and (V-I) 0 that is dispersionless. Assumption (2): A shape for this relation is obtained by following single stars through their pulsation cycle. Assumption (3): Since no single star cycles through all of the intrinsic colors expected for Cepheids, in practice a variety of trajectories need to be superposed by moving the narrow color-color loops formed by individual stars (of differing periods) back along reddening lines until they overlap and form an empirically non-linear but continuous (imposed minimum dispersion) sequence. Assumption (4): A zero point can be fixed by placing stars of independently known reddening (e.g., Galactic cluster Cepheids and very near-by field objects) into this relation. And finally, Assumption (5): Metallicity corrections can be found that consist of simple zero-point shifts on the colors as deduced by the authors from published theory. This formalism and calibration has been adopted in one form or another by the South African Group for all of their subsequent analysis of Magellanic Cloud data and their calibration of the PLC as they have applied it to the extragalactic distance scale (including most recently Laney & Stobie 1994).
We now illustrate the dangers inherent in each of these assumptions. We start with the generally accepted, linear form of the PLC. It is written twice below: once with the color (B-V) 0, and then again with the color (V-I) 0 as the temperature indicator:
We then equate these two expressions and regroup
like terms, eliminating MV, thereby leading to the
following equation, applicable to the color-color plane:
By claiming that for Cepheids there is a unique and dispersionless
relation between any two intrinsic colors (despite empirical evidence
to the contrary,
Cousins 1978a,
b)
the South African Group is
explicitly ignoring the period dependence in the above equations. The
tacit assumption then is that both colors are insensitive to gravity
effects, and therefore the combination of the equations given above
are forced by them to be degenerate in period (i.e.,
While ignoring the period dependence in a second PLC relation may be a
convenient and simplifying first approximation to a difficult problem,
continuing on to add higher-order non-linear (curvature) terms, and
also use theoretical displacements of the origin (attributed to
metallicity effects) seems to be, at the very least, somewhat
premature.
Furthermore, the validity of Assumption (2) is questionable. It
explicitly equates the instantaneous, time-dependent behavior (of
luminosity and color) of an individual Cepheid of fixed mass,
period, and dynamically evolving surface gravity (as it cycles through
radius, luminosity and temperature with phase) with the time-averaged
properties of an ensemble of stars each having different masses,
different mean surface gravities, temperatures and periods. However,
there is no a priori justification for assuming that the
behavior of a single star during its cycle is anything more than
qualitatively indicative of the way in which the (time-averaged
properties of the) instability strip are mapped in luminosity and
color when changing from star to star. For example, no one seriously
considers determining the slope of the color term
Despite the small formal uncertainties in the resulting PLC fit
determined by this methodology (see
Feast 1991
for a recent example)
it should be emphasized that almost all methods which ``correct'' for
differential absorption within the PL relation will give rise to a PLC
of smaller (apparently intrinsic) scatter. Furthermore, the
determination of the color term
Because of its inherent complexity we are not in a position to solve
the reddening problem at this time; however, its impact on the distance
scale can be minimized by accepting that reddening is a systematic
problem, and realizing that it can be dealt with effectively by at
least three available means, which involve (1) moving as far to the
infrared as is practical, so as to reduce the extinction problem to
the level of other systematic and random errors, (2) combining
multiwavelength (visual to near-infrared) data for significant numbers
of Cepheids in a given galaxy, and determining the ensemble-averaged
extinction (and true modulus) using an independently calibrated
wavelength-dependent extinction law, or (3) using reddening-free
formulations which are designed to cancel out any and all extinction
on a star-by-star basis, without ever attempting to determine the
amount explicitly. Each of these alternatives is dealt with in some
detail in this review and its other appendices.
It is clear however that if an explicit solution for individual
reddenings is ever to be found, it will most likely come through an
investigation of extragalactic, not Galactic, Cepheids. The LMC has
acted as the focal-point for calibration purposes for some years now,
primarily because it has a large population of Cepheids with known
periods, and because it is sufficiently close that accurate photometry
can be obtained for its stars with relative ease. However, the LMC
Cepheids do individually suffer from some degree of extinction
internal to the LMC itself, and also varying amounts of foreground
Galactic extinction. The SMC has a similarly large population of
Cepheids. Although it is somewhat further away than the LMC, it is not
excessively so. And while it is generally accepted that in comparison
to the LMC the extinction is less internal to and in front
of the SMC,
it is now known (primarily from studies of the Cepheids!) that the
back-to-front geometry of the SMC is such that appreciable
differential modulus residuals are affecting the magnitudes. Any
empirical correlations between reddening-corrected colors and
extinction-corrected magnitudes would have this (geometric) noise to
contend with.
We suggest then that the best place for future work on the intrinsic
calibration problem is not the Magellanic Cloud system, but the Local
Group galaxy IC 1613. The foreground reddening to IC 1613 is, by all
estimates, very low and probably quite uniform, considering the high
Galactic latitude and small angular size of this galaxy as compared to
either of the Magellanic Clouds. In a like way to the
SMC the
extinction internal to IC 1613 also appears to be quite small. With
the surveys of
Sandage (1971) and
Carlson & Sandage (1990)
now complete, there is also a sizable population of Cepheids in IC 1613 to
work with. Of course crowding is more of a problem for photometry of
individual Cepheids in IC 1613 as compared to the LMC, for example;
but considering the success had with photoelectric photometers using
aperture sizes in excess of 10 arcsec when working on LMC / SMC Cepheids
it is realistic to expect that point-spread-function fitting routines
(effectively working on one-arcsec scales) will be able to do at least
as well. And the quality of BVRI light curves obtained for
Cepheids in NGC 300
(Freedman et al.
1992),
at a distance about three times further than IC 1613, seems to bear out this expectation.
Of course, IC 1613 is only one galaxy, representing a single
cut of
metallicity, still the Cepheid calibration is at that stage where even
one solid observational study can contribute a great deal to the
effort.
 logP
+
logP
+  (B-V) 0 +
(B-V) 0 + 
 logP
+
logP
+  (V-I)
0 +
(V-I)
0 + 
 -
-  ) /
) /  ] logP +
[
] logP +
[ /
/  ] (V-I)
0 + [(
] (V-I)
0 + [( -
-  ) /
) /  ]
]
 =
=  ). The consequences of such
an assumption are two-fold: not only are the derived reddenings wrong at
the level that surface-gravity difference effects from star to star are
manifest in the time-averaged colors, but the inferred intrinsic colors are
deceiving. If the South African calibration tracks the ridge line of
the true instability strip in the color-color plane then the following
statements can be made: Obviously the stars residing on the constant
period lines intrinsically to the blue of the mean will systematically
have their reddenings underestimated by this method (while stars whose
intrinsic colors have them on the red side of the instability strip
will have their reddenings overestimated). But moreover, as
Figure 12
illustrates, should the relative slope of the constant-period line be
less than the slope of the reddening line in the color-color plot,
then the inferred intrinsic position of the stars within the
instability strip will be totally inverted from their true mapping!
). The consequences of such
an assumption are two-fold: not only are the derived reddenings wrong at
the level that surface-gravity difference effects from star to star are
manifest in the time-averaged colors, but the inferred intrinsic colors are
deceiving. If the South African calibration tracks the ridge line of
the true instability strip in the color-color plane then the following
statements can be made: Obviously the stars residing on the constant
period lines intrinsically to the blue of the mean will systematically
have their reddenings underestimated by this method (while stars whose
intrinsic colors have them on the red side of the instability strip
will have their reddenings overestimated). But moreover, as
Figure 12
illustrates, should the relative slope of the constant-period line be
less than the slope of the reddening line in the color-color plot,
then the inferred intrinsic position of the stars within the
instability strip will be totally inverted from their true mapping!
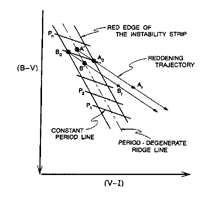 Figure 12. Projection of the PLC into the
(B - V) - (V - I) color-color plane. As shown by the foregoing
equation involving (B-V), (V-I) and log(P) in Section 15, the projection
of the Cepheid PLC into the color-color plane results in a finite region
crossed by lines of constant period and bounded by the blue and red
edges of the instability strip. Representative reddening trajectories
are shown passing through the ends of a typical constant-period line
such that their projection back onto the central ridge line
illustrates the reddening errors made if one erroneously adoptes a
dispersionless relation between these two colors. Notice how a
Cepheid that intrinsically resides on one (red/blue) edge of the
instability strip gets forced to the opposite (blue/red) edge by this
incorrect procedure.
Figure 12. Projection of the PLC into the
(B - V) - (V - I) color-color plane. As shown by the foregoing
equation involving (B-V), (V-I) and log(P) in Section 15, the projection
of the Cepheid PLC into the color-color plane results in a finite region
crossed by lines of constant period and bounded by the blue and red
edges of the instability strip. Representative reddening trajectories
are shown passing through the ends of a typical constant-period line
such that their projection back onto the central ridge line
illustrates the reddening errors made if one erroneously adoptes a
dispersionless relation between these two colors. Notice how a
Cepheid that intrinsically resides on one (red/blue) edge of the
instability strip gets forced to the opposite (blue/red) edge by this
incorrect procedure.
 , in the PLC
by looking at how an individual star changes its luminosity with color
(as a function of phase). Likewise, no one should seriously use the
color-color trajectory of individual Cepheid to calibrate the complex
mapping of a variety of stars and their PLC into the color-color
plane.
, in the PLC
by looking at how an individual star changes its luminosity with color
(as a function of phase). Likewise, no one should seriously use the
color-color trajectory of individual Cepheid to calibrate the complex
mapping of a variety of stars and their PLC into the color-color
plane.
 in the PLC depends sensitively
and explicitly on there being accurate individual reddenings for each
of the stars entering the calibration. For the reasons outlined above,
we do not believe that an accurate value of
in the PLC depends sensitively
and explicitly on there being accurate individual reddenings for each
of the stars entering the calibration. For the reasons outlined above,
we do not believe that an accurate value of  has yet been
determined precisely because the systematics of determining reddenings
have yet to be fully appreciated or adequately addressed.
has yet been
determined precisely because the systematics of determining reddenings
have yet to be fully appreciated or adequately addressed.
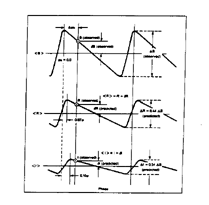 Figure 13. Cepheid light curves as a
function of observed wavelength. A schematic illustration of the relative
decrease in amplitude and shift in phase associated with observing
Cepheids at progressively longer wavelengths (adapted from
Freedman 1988a).
Figure 13. Cepheid light curves as a
function of observed wavelength. A schematic illustration of the relative
decrease in amplitude and shift in phase associated with observing
Cepheids at progressively longer wavelengths (adapted from
Freedman 1988a).
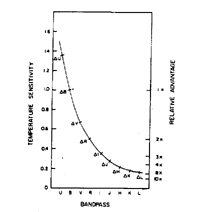 Figure 14. Amplitudes and/or instability
strip width for Cepheids as a function of increasing wavelength (adapted
from Freedman, Grieve &
Madore 1985).
The large relative amplitudes
(large strip widths) at blue and ultraviolet wavelengths are due to
the higher sensitivity of monochromatic surface brightness to
temperature variations at short wavelengths; low amplitudes (small
instability strip widths) in the red and near-infrared are dominated
by the small percentage changes in surface area, driven by the radial
pulsation.
Figure 14. Amplitudes and/or instability
strip width for Cepheids as a function of increasing wavelength (adapted
from Freedman, Grieve &
Madore 1985).
The large relative amplitudes
(large strip widths) at blue and ultraviolet wavelengths are due to
the higher sensitivity of monochromatic surface brightness to
temperature variations at short wavelengths; low amplitudes (small
instability strip widths) in the red and near-infrared are dominated
by the small percentage changes in surface area, driven by the radial
pulsation.
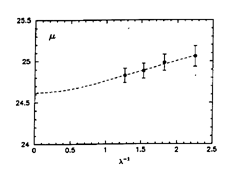 Figure 15. BVRI apparent distance moduli
for Cepheids in M33, plotted as a function of inverse wavelength (1/
Figure 15. BVRI apparent distance moduli
for Cepheids in M33, plotted as a function of inverse wavelength (1/
 in
inverse microns) from
Freedman, Wilson & Madore
(1991).
The broken
line is a fit of a Galactic extinction law to the data, with E (B-V) =
0.10 mag.
in
inverse microns) from
Freedman, Wilson & Madore
(1991).
The broken
line is a fit of a Galactic extinction law to the data, with E (B-V) =
0.10 mag.
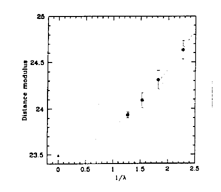 Figure 16. BVRI apparent distance moduli
plotted as a function of inverse wavelength for Cepheids in
NGC 6822.
The filled
triangle marks the true modulus = intercept of the fit at the origin
1/
Figure 16. BVRI apparent distance moduli
plotted as a function of inverse wavelength for Cepheids in
NGC 6822.
The filled
triangle marks the true modulus = intercept of the fit at the origin
1/  = 0.0 for E (B-V) =
0.21 ± 0.03 mag (from
Gallart et al. 1996).
= 0.0 for E (B-V) =
0.21 ± 0.03 mag (from
Gallart et al. 1996).