The absolute calibration of colors and/or magnitudes of Cepheids is obviously wrought with many traps and uncertainties in methodology and procedure. One very appealing way to proceed is in an implicit formulation and calibration of the problem. Rather than explicitly solving for the reddening/extinction star by star, one can begin quite differently: First adopt a standard reddening line for the color system being employed, then form linear combinations of the magnitudes and colors so that the numerical quantity formed cancels the reddening (star by star) without ever explicitly determining it. Then this formulation can be used both for the calibration objects and for the target Cepheids. Forming this reddening-free magnitude directly parallels the more common reddening-free application to colors, such as Q = (U-B) - X (B-V) as defined by Johnson (1963). An example follows.
Suppose that the observed magnitude of the Cepheid is V and its
apparent color is (B-V). As in the standard procedure, where
individual reddening corrections are made, we assume that the ratio of
total-to-selective absorption is known from independent
determinations, and that its value is 
V - R
(B-V). A simple expansion of the relevant terms shows that for small
amounts of reddening the numerical value of W is independent of
extinction, and equal to the value that would be calculated if the
intrinsic magnitudes and colors were known (which they now need not
be). That is, by definition,
There exists some confusion in the literature as to the real
motivation and physical justification for creating W for
Cepheids. W in fact is a reddening-free quantity for stars, not
exclusively for Cepheids. It is strictly defined by the properties of
the interstellar medium, not by any properties of the stars to which
it is to be applied. One is not at liberty, for example, to change the
value of R from its normal value of 3.3, unless that correction
derives from an independent study of the extinction law
itself. Accordingly, with the exception of the small known dependence
of R on (B-V) and E (B-V) itself, (manifest as
non-linear curvature terms at large values of these quantities; true
for all applications of reddening corrections, not just W) one cannot
manipulate the form of W at all.
The reason for some of the confusion dates back to a similar
realization of the PLC introduced by
van den Bergh (1975),
also called
W. In that first appearance of a linear combination of V
and (B-V) the complete reddening independence of the function
was not fully implemented, as will become clear now. In the following
discussion we will use WBFM and WvdB =
V -
For Cepheids one can begin to see what WBFM is, both
in terms of its parent relationship, the period-luminosity-color
relation, and in terms of its own definition. Adopting a linearized form
of the period-luminosity-color relation we have,
where mod0 is the true distance modulus. By definition,
so, by substituting the period-luminosity-color relation into the definition
of WBFM we get
or, expanding the reddening terms, regrouping and cancelling, we get
since, by definition, AV equals R E
(B-V). For Cepheids, the WBFM can be reformulated
as a period-luminosity-color relation. Here it must be emphasized that the
zero point
Here now is the point of confusion. van den Bergh (1969) noted the
numerical similarity of R = 3.2 to the then espoused value of
In order to illuminate the differences between the
WBFM and WvdB ,
Figure 11 portrays
the mapping of the PLC from its projection onto the traditional
color-magnitude diagram (as an instability strip) and then into the
three ``period-luminosity'' planes.
The upper left-hand panel shows a portion of the Cepheid instability
strip in a color-magnitude diagram. The upwardly slanting solid lines
give the red and blue edges of the strip, while the heavy
downward-slanting lines labeled P1 and P2 are
representative lines of constant period. Arrows indicate the slope of
a reddening/extinction line. The upwardly sloping broken line
indicates the apparent red edge of the instability strip as defined by
stars reddened away from the intrinsic line.
The horizontal broken lines leading from Panel 1 to Panel 2 show the
first mapping of the instability strip into the V-log P plane. The
sloping lines of constant period in Panel 1 now become vertical, with
downward extensions due to reddening increasing the apparent
dispersion at fixed period.
Panel 3 to the lower right shows the effect of forming
WvdB given a priori knowledge of the value of
Panel 4 shows the effect of forming WBFM. Since the
slope of a reddening line is well known from independent studies,
differential reddening has no effect on the width at constant
period. The only factor contributing to the width in
WBFM is the intrinsic width of the PLC (and as
mentioned earlier photometric errors in the magnitudes and colors, which
broaden all of the above relationships and projections).
Given Figure 11, it is perhaps worth noting
that in the presence of
differential reddening it is clearly inappropriate to determine the
value of
W0
(B-V) to distinguish between the differing definitions used by
Madore (1982)
and van den Bergh (1975),
respectively.
log P
+
(B-V)0 + 
+ mod0 + AV
V - R
(B-V)
log
P +
(B-V) 0 + + mod0 + AV - R (B-V)
log
P + [
- R] (B-V) 0 + +
mod0
and the slope of the period dependence in the WBFM
formulation of the period-luminosity-color relation are
identical to their counterparts in the V formulation; only the
coefficient multiplying the intrinsic color changes from to
-
R] = 2.7, and
at that point he chose his definition of WvdB V - (B-V)
which is quite a different approach. WBFM has the
advantage of being a strictly-defined, reddening-free magnitude
adopting a well-determined quantity R, which does not attempt to
anticipate the a priori unknown value of . Furthermore,
residual scatter in the WBFM - log P relation is also
thereby distinctly of interest in its own right. Unlike scatter in the
observed PL or PC relations, scatter in the WBFM - log
P relation cannot be due to reddening effects, be they
differential or total. One is not at liberty to adjust the coefficient
R for various samples of Cepheids (to minimize the scatter in
the residual, for example) unless there is independent evidence
that the ratio of total-to-selective absorption is different for that
particular galaxy. The remaining scatter in a WBFM - log
P plot will be due to a combination of intrinsic (color?)
correlations and photometric errors. As is so often the case it will be
an understanding of the photometry and its quality that will ultimately
limit our understanding of the intrinsic interrelations.
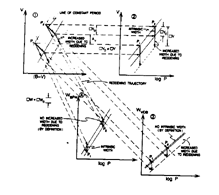Figure 11. Projecting the observed
instability strip,
in the presence of reddening. (1) In the upper left panel the
instability strip superimposed on the PLC is shown projected into the
color-magnitude plane. Lines of constant period (P1
and P2) are shown as thick solid lines slanting down
to the right. The blue and red edges of the instability strip are shown
as thinner solid lines sloping down to the left. Arrows indicated the
magnitude and direction of reddening which acts to increase the apparent
width of the distribution by systematically scattering points to redder
colors and to fainter magnitudes. A dashed line parallel to but fainter than
the red edge of the instability strip illustrates the bounds of this
effect. (2) The upper right panel is constructed from the first panel
by projecting the instability strip and the reddening vectors into the
Period-Luminosity plane. There is a systematic increase in the width
of the apparent PL relation due to extinction, as in the CM diagram.
(3) If the slopes of the lines of constant period are known a
priori, then the projection of the instability strip into the
WvdB - log P plane can be performed. By
definition, the intrinsic width goes to zero in this projection, but
because the slope of the lines of constant period are not exactly
parallel to the reddening trajectory, extinction does project into this
plane and will widen the relation, and systematically shift the ridge
line. (4) Since reddening trajectories are, in general, already
determined a priori, it is possible to project the instability
strip into the WBFM - log P plane where (by
definition) extinction effects are eliminated. In this case, however the
intrinsic width does still contribute to the dispersion, but the
disposition of the individual stars within this strip is not effected by
reddening.
the slope
of the lines of constant period in the PLC. As can be seen, the projected
width in the WvdB - log P plane is non-zero in the
presence of reddening. While the intrinsic width of the instability
strip does project to zero (by definition, once is known from
independent sources) there is residual widening due to reddening
by minimization of residuals, as would be the case in an unrestricted
application of a multi-linear regression fit to PLC
data, for instance. For the example at hand, one can see immediately
by inspection that a slope somewhere between the true value of
and the reddening slope R would give the minimum residuals plotted as
a function of period. The numerical value of that parameter for any
given set of Cepheids is however of no universal significance.