1.1. Basics of Quasar Spectra

Figure 1 illustrates many of the common features of a quasar spectrum. The relatively flat quasar continuum and broad emission features are produced by the quasar itself (near the black hole and its accretion disk). In some cases, gas near the quasar central engine also produces ``intrinsic'' absorption lines, most notably Ly, and relatively high ionization metal transitions such as C IV, N V, and O VI. These intrinsic absorption lines can be broad [thousands or even tens of thousands of km s<sup>-1</sup> in which case the quasar is called a broad absorption line (BAL) QSO], or narrow (tens to hundreds of km s<sup>-1</sup>). However, the vast majority of absorption lines in a typical quasar spectrum are ``intervening'', produced by gas unrelated to the quasar that is located along the line of sight between the quasar and the Earth.

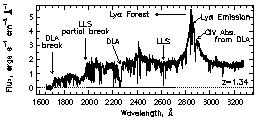
Figure 1. Typical spectrum of a quasar, showing the quasar continuum and emission lines, and the absorption lines produced by galaxies and intergalactic material that lie between the quasar and the observer. This spectrum of the z = 1.34 quasar PKS0454+039 was obtained with the Faint Object Spectrograph on the Hubble Space Telescope. The emission lines at ~ 2400 Å and ~ 2850 Å are Ly and Ly. The Ly forest, absorption produced by various intergalactic clouds, is apparent at wavelengths blueward of the Ly emission line. The two strongest absorbers, due to galaxies, are a damped Ly absorber at z = 0.86 and a Lyman limit system at z = 1.15. The former produces a Lyman limit break at ~ 1700 Å and the latter a partial Lyman limit break at ~ 1950 Å since the neutral Hydrogen column density is not large enough for it to absorb all ionizing photons. Many absorption lines are produced by the DLA at z = 0.86 (C IV 1548, for example, is redshifted onto the red wing of the quasar's Ly emission line).

A structure along the line of sight to the quasar can be described by its neutral Hydrogen column density, N(HI), the number of atoms per cm². N(HI) is given by the product of the density of the material and the pathlength along the line of sight through the gas. Each structure will produce an absorption line in the quasar spectrum at a wavelength of _obs = _rest (1 + z_abs), where z_abs is the redshift of the absorbing gas and _rest = 1215.67 Å is the rest wavelength of the Ly transition. Since z_abs < z_QSO, the redshift of the quasar, these Ly absorption lines form a ``forest'' at wavelengths blueward of the Ly emission. The region redward of the Ly emission will be populated only by absorption through other chemical transitions with longer _rest. Historically, absorption systems with N(HI) < 10^17.2 cm^-2 have been called Ly forest lines, those with 10^17.2 < N(HI) < 10^20.3 cm^-2 are Lyman limit systems, and those with N(HI) > 10^20.3 cm^-2 are damped Ly systems. The number of systems per unit redshift increases dramatically with decreasing column density, as illustrated in the schematic diagram in Figure 2. Lyman limit systems are defined by a sharp break in the spectrum due to absorption of photons capable of ionizing HI, i.e. those with energies greater than 13.6 eV. The optical depth, , of the break is given by the product N(HI) , where the cross section for ionization of Hydrogen, = 6.3 x 10^-18 (E / 13.6 eV)^-3 cm², (and the flux is reduced by the factor e^-). The energy dependence of leads to a recovery of the Lyman limit break at higher energies (shorter wavelengths), unless N(HI) >> 10^17.2 cm^-2 (see Figure 1).

Figure 2. The column density distribution of Ly clouds, f(N(HI), roughly follows a power law over ten orders of magnitude; there are many more weak lines than strong lines. The column density regions for the three categories of systems are shown: Ly forest, Lyman limit, and damped Ly. The term ``Ly forest'' has at times been used to refer to metal-free Hydrogen clouds, perhaps those with N(HI) < 1016 cm-2, but now metals have been found associated with weaker systems down to the detection limit.

The curve of growth describes the relationship between the equivalent width of an absorption line, W, (the integral of the normalized profile) and its column density, N. Figure 3 shows that for small N(HI) the number of absorbed photons, and therefore the flux removed, increases in direct proportion to the number of atoms. This is called the linear part of the curve of growth. As N is increased the line saturates so that photons are only absorbed in the wings of the lines; in this regime the equivalent width is sensitive to the amount of line broadening (characterized by the Doppler parameter b), but does not depend very strongly on N(HI). This is the flat part of the curve of growth. Finally, at N(HI) > 10^20.3 cm^-2, there are enough atoms that the damping wings of the line become populated and the equivalent width increases as the square root of N(HI), and is no longer sensitive to b.

Figure 3. Illustration of the different regimes of the curve of growth. The middle panel shows the curve of growth for the Ly transition, relating the equivalent width, W, of the absorption profile to the column density, N(HI). The different curves represent four different values of the Doppler parameter: b = 13, 23, 53, and 93 km s-1. The upper panel shows absorption profiles with Doppler parameter b = 23 km s-1 for the series of neutral hydrogen column densities N(HI) = 1012 - 1020 cm-2. The thick (thin) curves correspond to the filled (open) points on the b = 23 km s-1 curve of growth (middle panel), starting at N(HI) = 1012 cm-2. For N(HI) < 1013 cm-2, known as the linear part of the curve of growth, the equivalent width does not depend on b. The lower left panel shows that, at fixed N(HI), the depth of the profile is smaller for large b, such that the equivalent width remains constant. On the flat part of the curve of growth, profiles are saturated and the equivalent width increases with b for constant N(HI). For N(HI) > 1020 cm-2, the profile develops damping wings, which dominate the equivalent width.

In addition to the Ly (1s -> 2p) and higher order (1s -> np) Lyman series lines, quasar spectra also show absorption due to different ionization states of the various species of metals. Figure 1 illustrates that the damped Ly system at z = 0.86 that is responsible for the Ly absorption line at _obs = 2260 Å and a Lyman limit break at _obs = 1700 Å also produces absorption at _obs = 2870 Å due to the presence of C IV in the absorbing gas at that same redshift. Like many of the strongest metal lines seen in quasar spectra, C IV is a resonant doublet transition due to transitions from ²S_1/2 energy levels to the ²P_1/2 and to the ²P_3/2 energy levels. (The left superscript ``2'' represents the number of orientations of the electron spin, the letter S or P represents the total orbital angular momentum, L, and the right subscript represents the total angular momentum, J.) Doublet transitions are easy to identify. The dichotomy between rest wavelength and redshift is resolved because the observed wavelength separation of the doublet members increases as 1 + z.

Table 1 lists some of the metal lines that are commonly detected for intervening absorption systems. Many of these are only strong enough to be observable for quasar lines of sight that pass through the higher N(HI) regions of galaxies.

Table 1. Common Transitions

Transition	rest [Å]
LL	~ 912
Ly	972.537
Ly	1025.722
Ly	1215.670
Si IV 1393	1393.755
Si IV 1402	1402.770
C IV 1548	1548.195
C IV 1550	1550.770
Fe II 2382	2382.765
Fe II 2600	2600.173
Mg II 2796	2796.352
Mg II 2803	2803.531